DH算法是第一个密钥交换算法，也是第一个得到形式化描述的公钥密码算法。
群论
DH密钥交换算法基于数学中的群论，群论也是当今大多数公钥密码的基础。
要使集合及其运算成为一个群，需要满足以下性质：
- 封闭性：群中两个元素运算的结果仍是集合中的元素。比如，对于群中的两个元素a和b，a*b也是群中的元素。
- 结合律：多个元素同时进行运算时，可以按任何顺序执行运算。比如，对于群元素a，b和c，a(bc)和(ab)c运算得到的是相同的群元素。
- 单位元：群中有且仅有一个元素是单位元，单位元与群中任一元素运算时都不会改变该元素。例如，我们在乘法群中将单位元定义为1，那么对于任何群元素a，都有a*1=a。
- 逆元：群中的元素均有逆元，群元素及其逆元的运算结果等于单位元。所有的群元素都存在逆元。比如，对于任何群元素a，都存在一个逆元素
，使得
。
模乘
DH密钥交换算法使用模乘这种特殊运算。
模运算可以参考我之前写的博客
密码学学习笔记(七)：Modular arithmetic - 模算数_kingofyb的博客-CSDN博客、
DH密钥交换
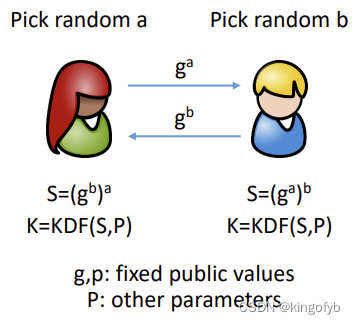
没有共享密钥的双方可以使用此协议建立共享密钥。
Alice随机挑选在里的a, 计算
mod p并将其发送给Bob。
Bob随机挑选在里的b, 计算
mod p并将其发送给Alice。
现在Alice知道a和所以她可以计算：
mod p
Bob知道b和所以他可以计算同样的S：
mod p
他们有一个共同的秘密𝑆 现在，可以使用KDF计算共享密钥。
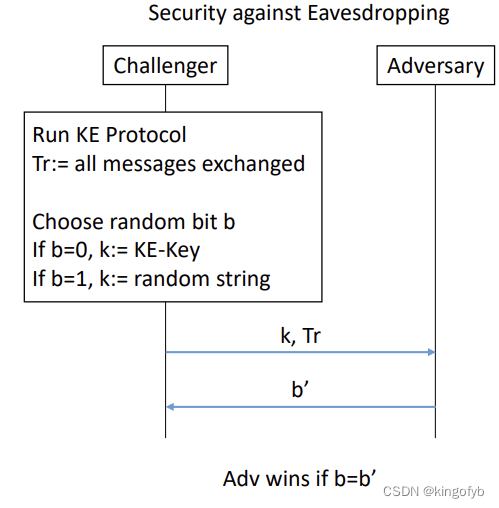
密钥交换安全性
- 防窃听安全：
对手可以看到所有通信，并旨在区分密钥和随机密钥。在实践中，对手可能能够拦截和修改通信。比如中间人（MitM）攻击。 - 针对MitM攻击的安全性：
对手可以查看和修改（删除、添加、更改）通信，并旨在区分密钥和随机密钥
DH密钥交换安全性
根据DH密钥交换算法的工作原理，算法参与者需要协商一个素数p和群生成元g作为公共参数。素数p应该尽可能越大越好。由于DH密钥交换算法的安全性基于离散对数问题的困难性，因此对离散对数问题的最佳攻击直接影响到DH算法的安全性。在实践中，通常将p设置为2048比特的素数。
𝑔, 𝑝 是公开的，窃听者也会得到
对于大模量𝑝:
- 用
很难计算得出a或者b - 离散对数（DL）问题
- 用
- 计算Diffie-Hellman（CDH）问题
- 用
所以这两个短暂的秘密𝑎, 𝑏 以及最终共享的秘密𝑆 对于窃听者来说很难计算𝑆 “看起来很随意”
但是Diffie–Hellman不能保证身份验证，因此不能防止中间人攻击，因此Diffie–Hellman必须始终与身份验证机制一起使用
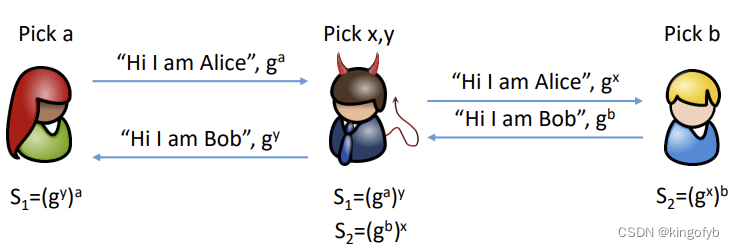
中间人对抗(Man In The Middle Attack)Diffie–Hellman
中间人（MitM）可以拦截和修改消息，向Alice假装自己是Bob，并向Bob假装自己是Alice
最后，Alice认为她正在与Bob分享一个秘密，Bob认为他正在与Alice分享一个机密，但两人都与密探分享了不同的秘密
如果Alice和Bob使用他们共享的秘密生成通信密钥，MitM可以读取所有内容
![linux学习(文件描述符)[11]](https://img-blog.csdnimg.cn/0c769e914642451ba66db0c9a4fe5baa.png)
