我们先搞清楚这几个概念

构造哈夫曼树的方法


将每种字符出现的频率先收集起来放在最上方,然后选择两个频率最小的增加到图中,并将他们的和作为他们的父节点,增加到图中,在最上方删除选择的两个节点(4和2),并添加他们的父节点6到最上方中
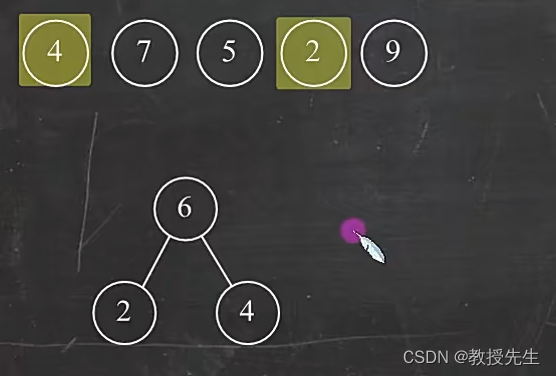
选择最上方当前两个最小的节点6和5,作为子节点构造得到他们的父节点5+6=11,在最上方删除5和6,增加11
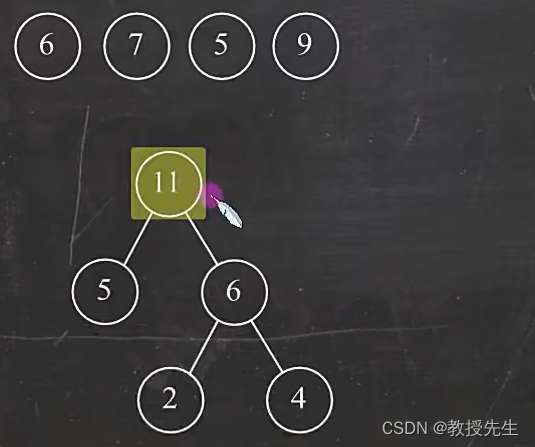
选择最上方当前两个最小的节点7和9,作为子节点构造得到他们的父节点7+9=16,在最上方删除7和9,增加16
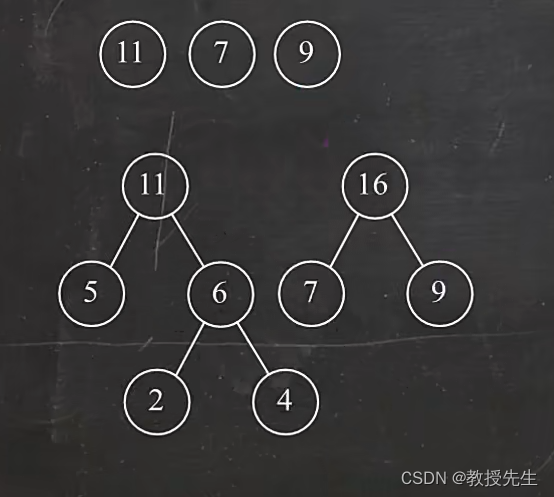
选择最上方当前两个最小的节点11和16,作为子节点构造得到他们的父节点11+16=27,在最上方删除11和16,增加27
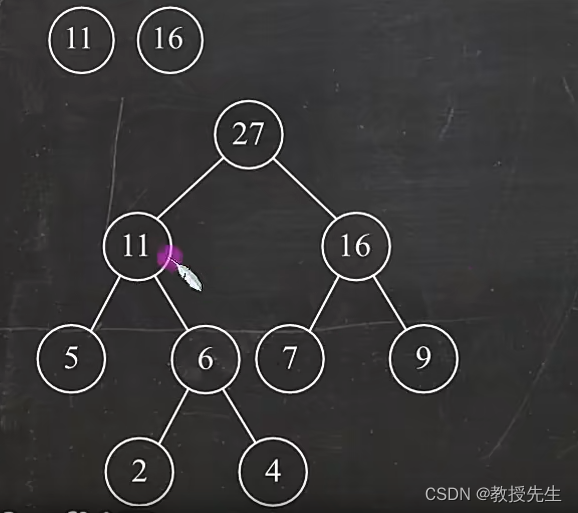
最终得到的这个图就是构造正确的 哈夫曼树

我们来看第二问 求出每个字符的哈夫曼编码
在题目中找到字符
a对应的频率是4 b对应的频率是7 c对应的频率是5 d对应的频率是2 e对应的频率是9
在原来的哈夫曼树中,左子树的边都赋值为0,右子树的边都赋值为1,从顶点27出发,沿着边寻找每个字符对应的频率,沿着边的足迹就是每个字符对于的哈夫曼编码值 结果如上图所示
第三问叫 求11000111000101011的对应电文,根据左图寻找每串数字对应字母的哈夫曼编码,互相比较得到结果

第四问叫求带权路径长度


树的带权路径长度: 树中所有叶结点的带权路径长度之和
这里左下方的5是这个树的一个叶节点(靠近树最外边缘的节点),他距离顶点27的边有2条(5—11和11—27)。 5叶节点的权值是5 乘边数 2 即(5*2)其他节点 以此类推,所有之和就是这个数的带权路径长度

我们来看一道例题

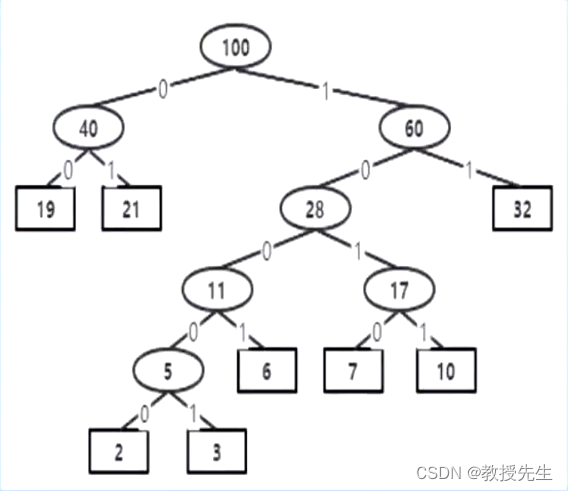
这个是他构造出来的哈夫曼树





![[附源码]Nodejs计算机毕业设计基于web的学生社团管理系统Express(程序+LW)](https://img-blog.csdnimg.cn/96bcc320595d4d6e80d9c54e73f02a2e.png)