概念

红黑树也是一种二叉搜索树，但是和avl树不同，它并不是依靠平衡因子来保证树的平衡的，而是通过颜色

红黑树每个节点中会存储颜色，分为红色和黑色，通过红黑树的限制条件，可以保证从根节点出发到叶子节点的每一条路径长度都不会是其他路径长度的两倍，以此达到接近平衡，保证了搜索的效率是log2（N）

性质

红黑树需要满足以下几点性质：

每个节点不是红色的就是黑色的
根节点必须是黑色的
如果一个节点是红色的，那么他的孩子节点必须是黑色的
每一条路径从根节点到叶子节点中的黑色节点的个数必须相同
所有的叶子节点（这里指的是空节点）都是黑色的

红黑树节点的定义

红黑树中的节点不仅需要定义左右孩子的指针，父节点的指针，自身存储的值，还要存储这个节点的颜色，这里通过枚举来存储
并且需要满足新创建的节点是红色的，因为如果要是创建的是黑色的，那么在插入的过程中很难保证性质四——每一条路径从根节点到叶子节点中的黑色节点的个数必须相同

节点定义代码

static class RBTreeNode {
        public RBTreeNode left;
        public RBTreeNode right;
        public RBTreeNode parent;
        public int val;
        public COLOR color;

        public RBTreeNode(int val){
            this.val = val;
            //新创建的节点默认是红色
            this.color = COLOR.RED;
        }
    }

COLOR枚举

package rbTree;

public enum COLOR {
    RED,BLACK
}

插入

在插入时和AVL树一样，要先按照平衡二叉树来进行遍历插入

先判断根节点是否为空，为空则直接插入
然后定义一个cur和parent，cur先为root，cur一直向下遍历。
如果val小于cur.val，cur就变成cur.left
大于的话就变成cur.right
如果等于，就说明已经有这个节点了，return false
在cur遍历的过程中，使parent始终为cur的上一个节点，使得当cur变成空时，能够记录上一个节点的位置
然后判断val和parent.val的大小关系，插到对应的位置上

RBTreeNode node = new RBTreeNode(val);
if(root == null){
    root = node;
    node.color = COLOR.BLACK;
    return true;
}
RBTreeNode parent = null;
RBTreeNode cur = root;
while(cur != null){
    if (cur.val < val){
        parent = cur;
        cur = cur.right;
    } else if (cur.val > val){
        parent = cur;
        cur = cur.left;
    } else {
        return false;
    }
}
if(parent.val < val){
    parent.right = node;
} else {
    parent.left = node;
}
node.parent = parent;
cur = node;

然后进行颜色的更改
因为默认插入的颜色是红色，因此如果父节点是黑色的话，那么就不违背任何性质，否则的话需要进行颜色的更改，因此循环的条件是parent不为空，parent的颜色是红色
定义parent的父节点grandfather节点
定义grandfather的另一个孩子节点uncle节点

while(parent != null && parent.color == COLOR.RED){
    //根不能是红色，所以一定有父节点
    RBTreeNode grandFather = parent.parent;
    if(parent == grandFather.left){
        RBTreeNode uncle = grandFather.right;

在这里分为以下几种情况：

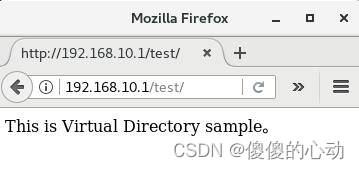
情况一

cur，parent为红，grandfather为黑，uncle存在且为红
在这里插入图片描述
此时cur和parent两个都是红色，因此不满足性质——如果一个节点是红色的，那么他的孩子节点必须是黑色的

此时如果把cur改成黑色，那么uncle这边就不满足性质—— 每一条路径从根节点到叶子节点中的黑色节点的个数必须相同

所以需要将parent和uncle都改成黑色节点

但是，这里还需要考虑grandfather的兄弟节点也会出现不满足性质—— 每一条路径从根节点到叶子节点中的黑色节点的个数必须相同，因此我们可以把grandfather改成红色的，这样就满足这个性质了

所以，如果grandparent是根节点，那么就不用改颜色了，如果不是根节点的话，我们就需要让grandparent变成红色的
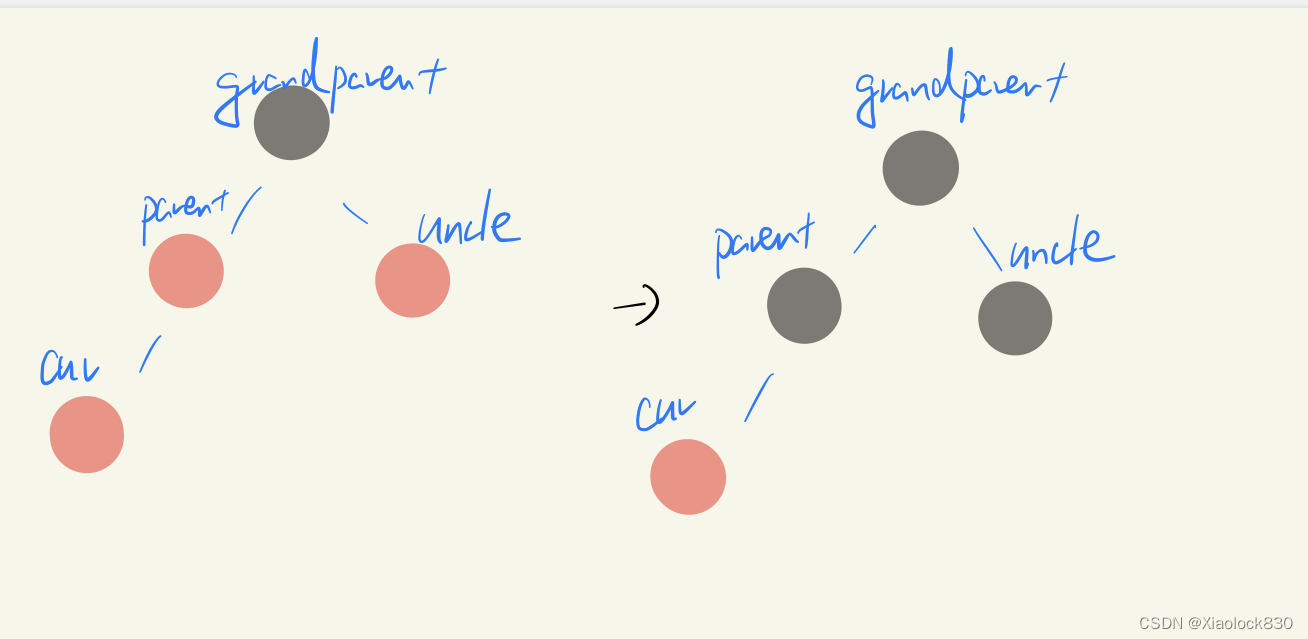
在这里插入图片描述
然后我们可以把grandparent看成cur，继续向上调整

if(uncle != null && uncle.color == COLOR.RED){
    parent.color = COLOR.BLACK;
    uncle.color = COLOR.BLACK;
    grandFather.color = COLOR.RED;

    //向上迭代
    cur = grandFather;
    parent = cur.parent;

情况二

cur和parent为红色，grandfather为黑色，uncle不存在或为黑色
这种情况就相当于情况一的相反情况，因此写在情况一的else中
情况二出现在下图这样，先是情况一进行调整，迭代后出现情况二
在这里插入图片描述

这时我们需要右单旋grandparent，然后将原来的grandparent变成红色，parent变成黑色
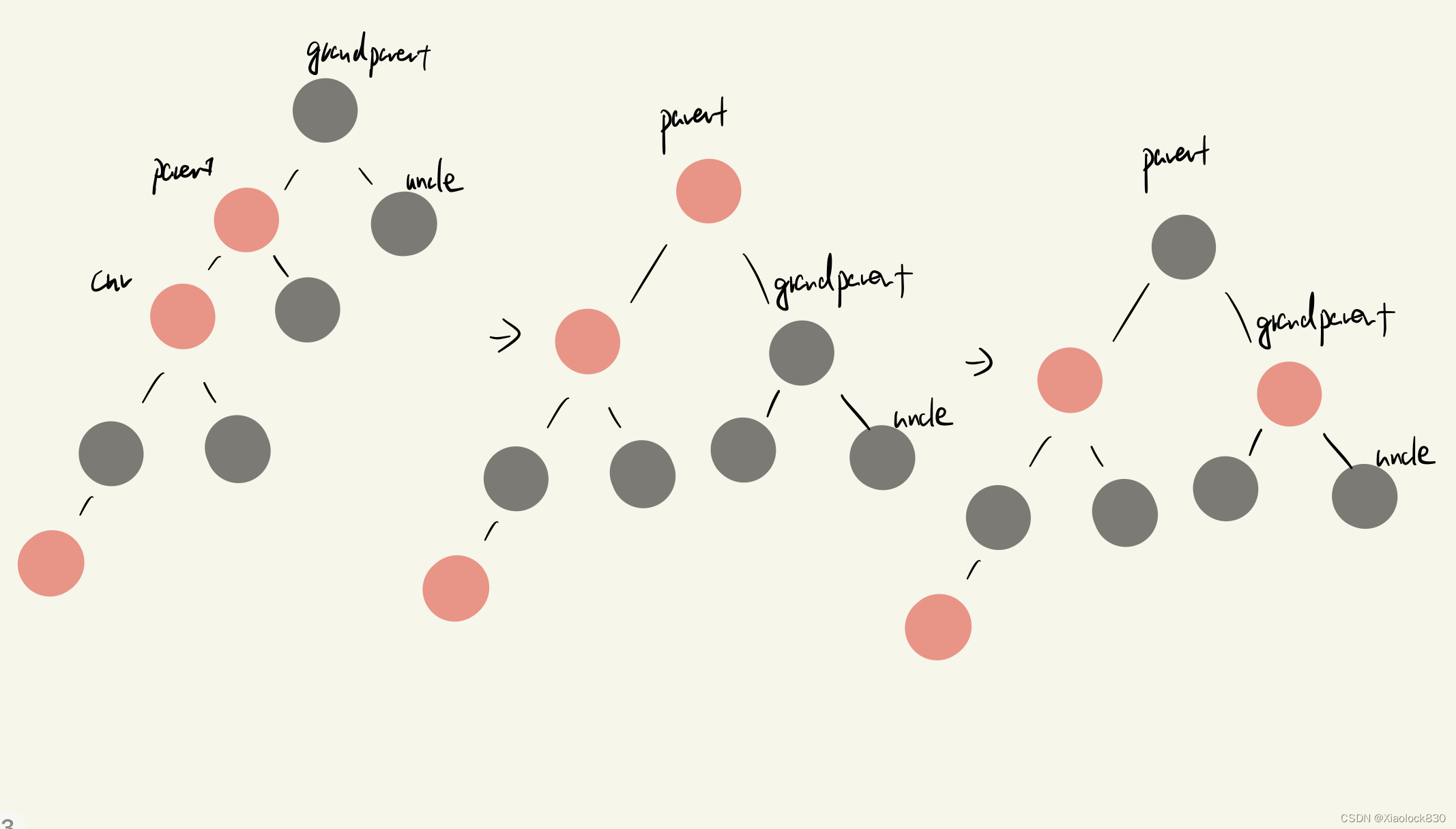
在这里插入图片描述
关于右单旋，这个在上一篇博客avl树中讲过，不会的可以去上一篇博客看

//uncle不存在或者是黑色
//情况二
rotateRight(grandFather);
grandFather.color = COLOR.RED;
parent.color = COLOR.BLACK;

右单旋：

private void rotateRight(RBTreeNode parent) {
    RBTreeNode subL = parent.left;
    RBTreeNode subLR = subL.right;

    parent.left = subLR;
    subL.right = parent;
    if(subLR != null) {
        subLR.parent = parent;
    }

    RBTreeNode pParent = parent.parent;

    parent.parent = subL;

    //检查是否parent为根节点
    if(parent == root){
        //使subL为根节点
        root = subL;
        root.parent = null;
    } else {
        //使得parent的原parent节点的孩子为subL
        if (pParent.left == parent) {
            pParent.left = subL;
        } else {
            pParent.right = subL;
        }
        subL.parent = pParent;
    }
}

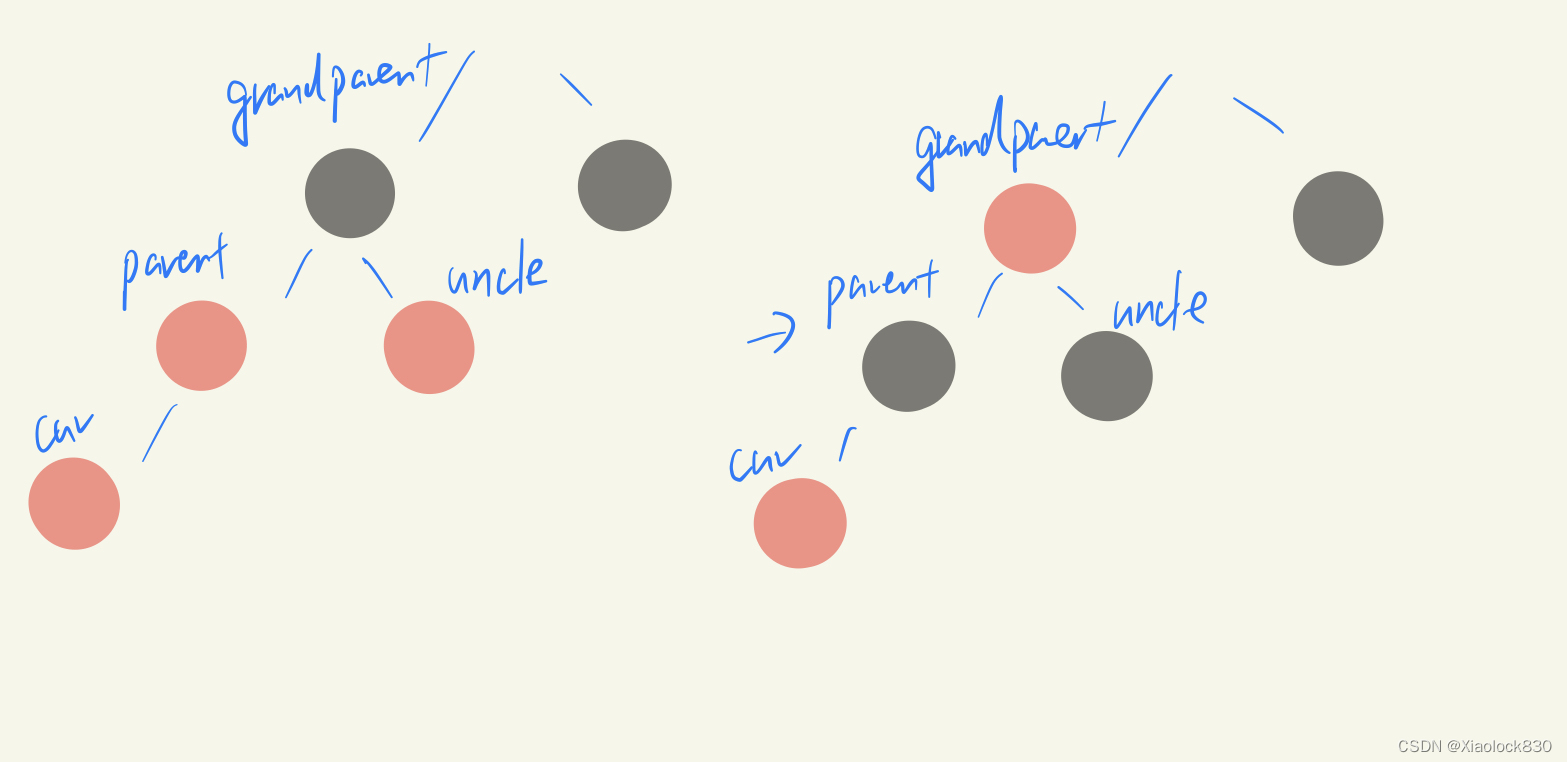
情况三

cur和parent为红色，grandfather为黑色，uncle不存在或者为黑色
情况三也是由下方迭代上来时，会出现的一种情况，例如下图
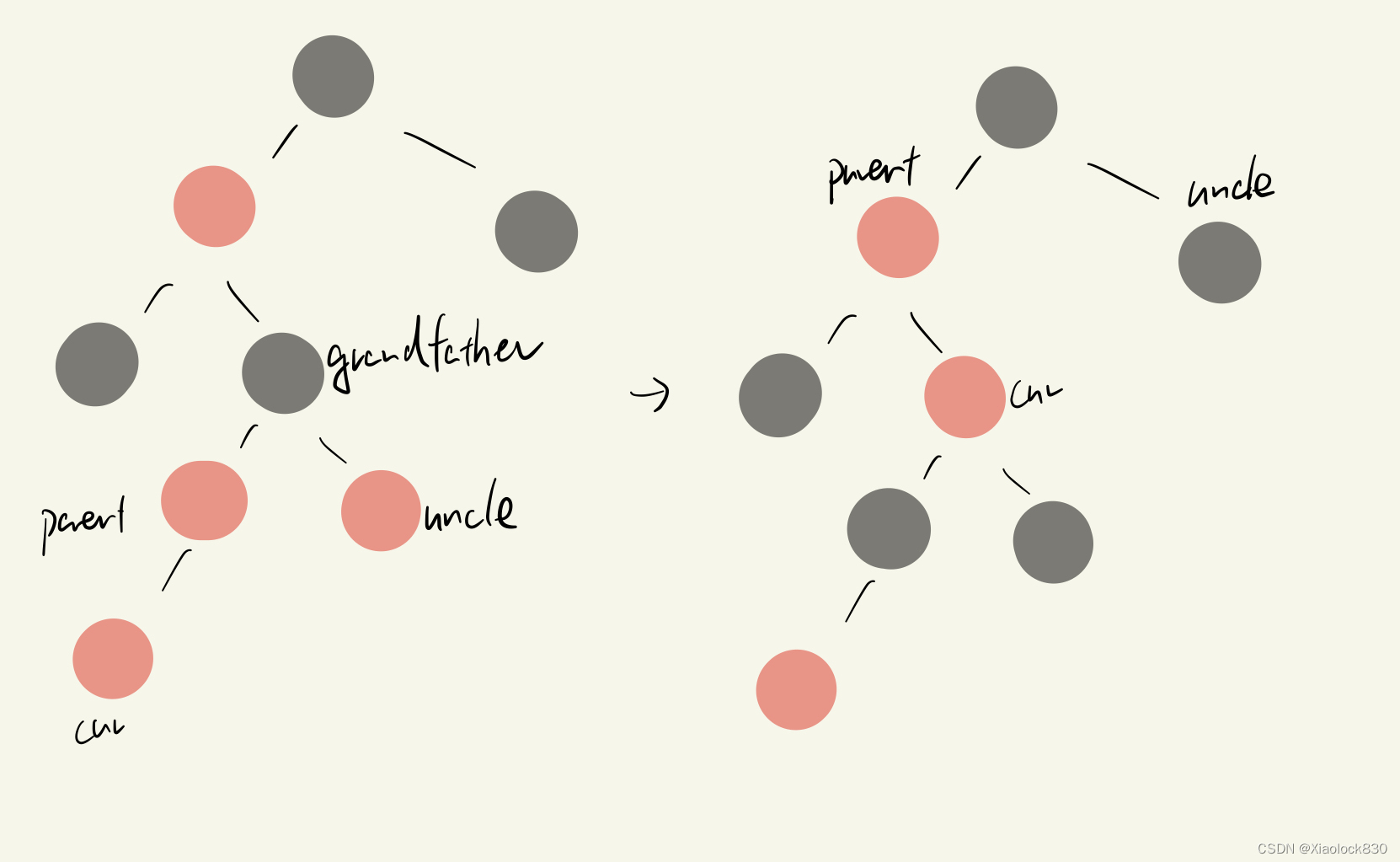
在这里插入图片描述
那么，我们需要将parent进行左单旋，这样问题就回到情况二了

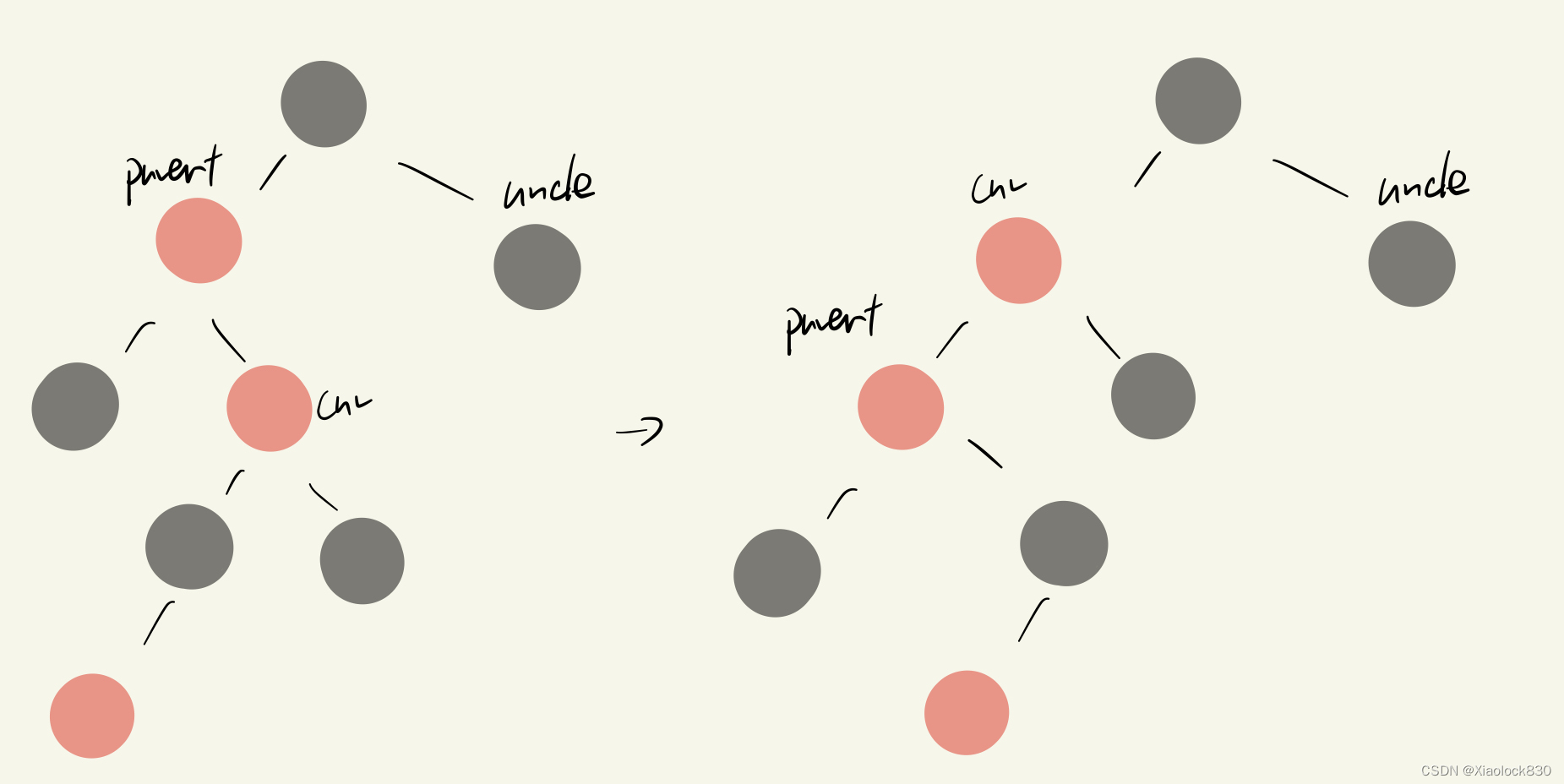
因此，我们只需要左单旋一下parent，然后让cur和parent交换一下位置，然后再用情况二来处理就可以了

//情况三
if(cur == parent.right){
    rotateLeft(parent);
    RBTreeNode tmp = parent;
    parent = cur;
    cur = tmp;
}//情况三变成情况二

//uncle不存在或者是黑色
//情况二
rotateRight(grandFather);
grandFather.color = COLOR.RED;
parent.color = COLOR.BLACK;

左单旋：

private void rotateLeft(RBTreeNode parent) {
    RBTreeNode subR = parent.right;
    RBTreeNode subRl = subR.left;

    parent.right = subRl;
    subR.left = parent;
    if(subRl != null){
        subRl.parent = parent;
    }

    RBTreeNode pParent = parent.parent;

    parent.parent = subR;

    if(root == parent){
        root = subR;
        root.parent = null;
    } else {
        if (pParent.left == parent){
            pParent.left = subR;
        } else {
            pParent.right = subR;
        }
        subR.parent = pParent;
    }
}

情况四，情况五，情况六

这三种情况就是uncle节点再parent的左侧的情况
情况四和情况一的处理是一样的

当cur是parent的right，就是情况五，那么和情况二处理方法类似，只是变成了左单旋grandparent
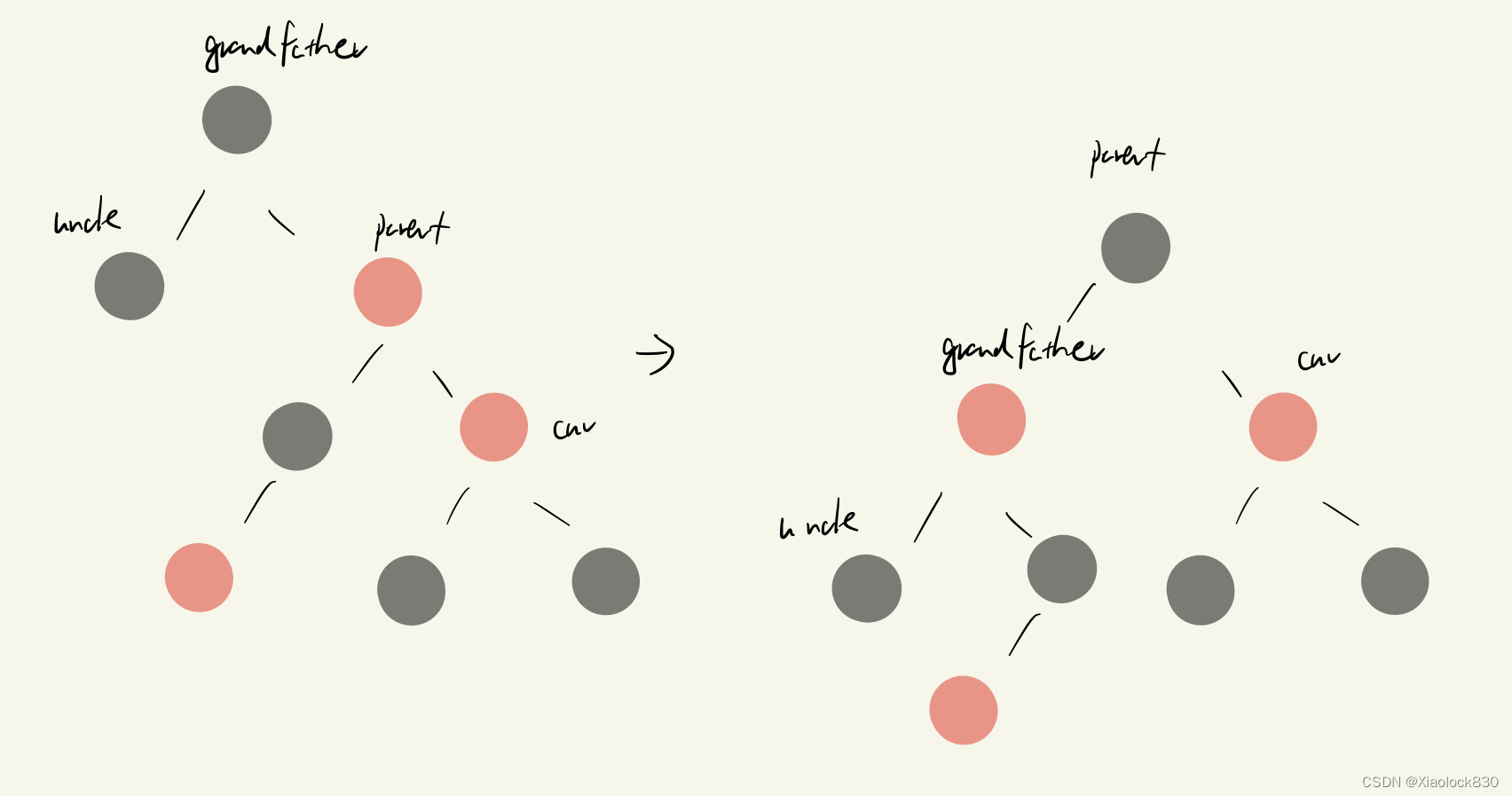
在这里插入图片描述

当cur是parent的left，就是情况六，那么和情况三处理方法类似，只是变成了右单旋parent
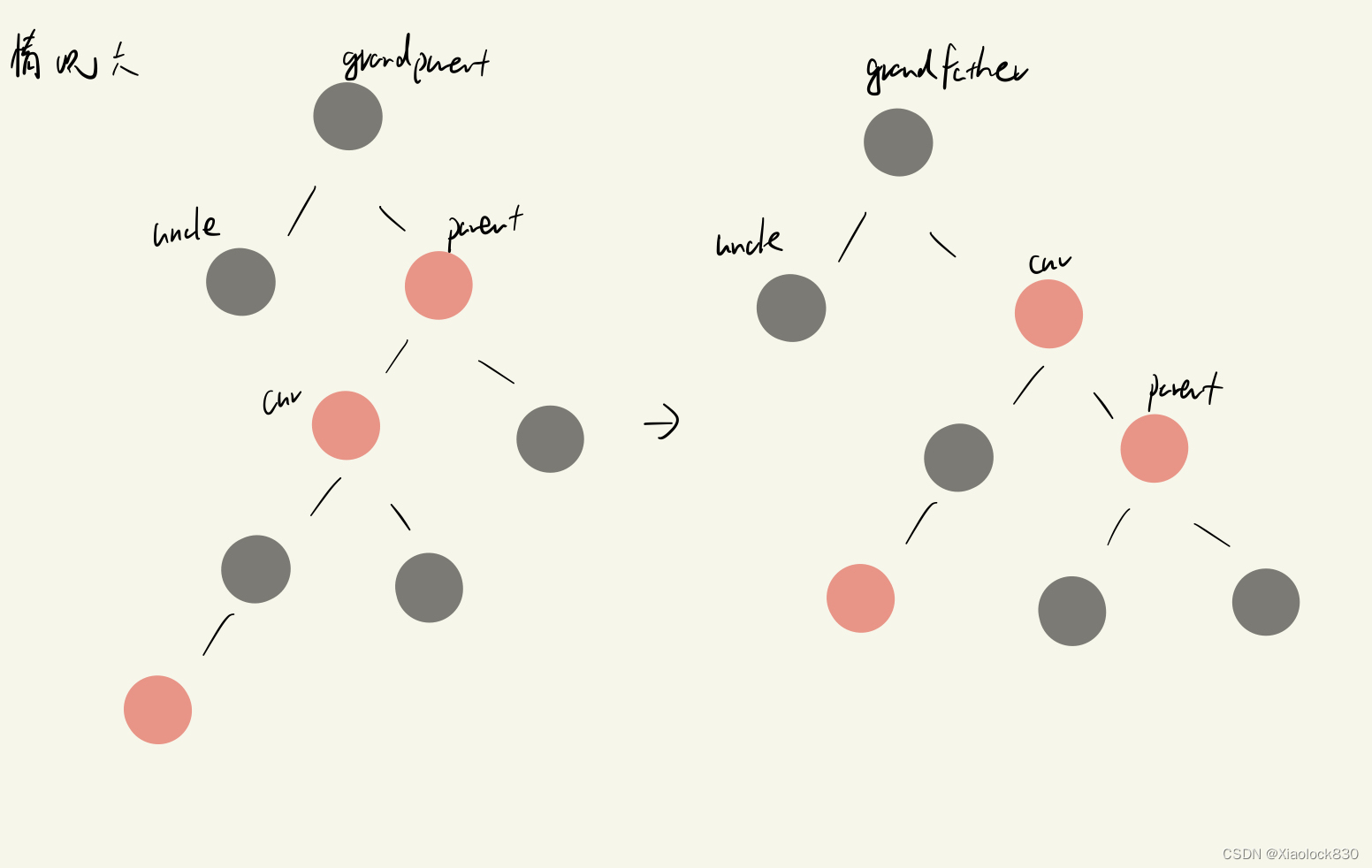
在这里插入图片描述

//parent == grandfather.right
RBTreeNode uncle = grandFather.left;
if(uncle != null && uncle.color == COLOR.RED){
	//情况四
    parent.color = COLOR.BLACK;
    uncle.color = COLOR.BLACK;
    grandFather.color = COLOR.RED;

    //向上迭代
    cur = grandFather;
    parent = cur.parent;
} else {
    //情况六
    if(cur == parent.left){
        rotateRight(parent);
        RBTreeNode tmp = parent;
        parent = cur;
        cur = tmp;
    }//情况五变成情况四

    //uncle不存在或者是黑色
    //情况五
    rotateLeft(grandFather);
    grandFather.color = COLOR.RED;
    parent.color = COLOR.BLACK;
}

插入的全部代码

public boolean insert(int val){
    RBTreeNode node = new RBTreeNode(val);
    if(root == null){
        root = node;
        node.color = COLOR.BLACK;
        return true;
    }
    RBTreeNode parent = null;
    RBTreeNode cur = root;
    while(cur != null){
        if (cur.val < val){
            parent = cur;
            cur = cur.right;
        } else if (cur.val > val){
            parent = cur;
            cur = cur.left;
        } else {
            return false;
        }
    }
    if(parent.val < val){
        parent.right = node;
    } else {
        parent.left = node;
    }
    node.parent = parent;
    cur = node;

    //调整颜色
    while(parent != null && parent.color == COLOR.RED){
        //根不能是红色，所以一定有父节点
        RBTreeNode grandFather = parent.parent;
        if(parent == grandFather.left){
            RBTreeNode uncle = grandFather.right;
            if(uncle != null && uncle.color == COLOR.RED){
                //情况一
                parent.color = COLOR.BLACK;
                uncle.color = COLOR.BLACK;
                grandFather.color = COLOR.RED;

                //向上迭代
                cur = grandFather;
                parent = cur.parent;
            } else {
                //uncle不存在或者是黑色
                //情况三
                if(cur == parent.right){
                    rotateLeft(parent);
                    RBTreeNode tmp = parent;
                    parent = cur;
                    cur = tmp;
                }//情况三变成情况二

                //情况二
                rotateRight(grandFather);
                grandFather.color = COLOR.RED;
                parent.color = COLOR.BLACK;
            }
        } else {
            //parent == grandfather.right
            RBTreeNode uncle = grandFather.left;
            if(uncle != null && uncle.color == COLOR.RED){
                //情况四
                parent.color = COLOR.BLACK;
                uncle.color = COLOR.BLACK;
                grandFather.color = COLOR.RED;

                //向上迭代
                cur = grandFather;
                parent = cur.parent;
            } else {
                //uncle不存在或者是黑色
                //情况六
                if(cur == parent.left){
                    rotateRight(parent);
                    RBTreeNode tmp = parent;
                    parent = cur;
                    cur = tmp;
                }//情况六变成情况五

                //情况五
                rotateLeft(grandFather);
                grandFather.color = COLOR.RED;
                parent.color = COLOR.BLACK;
            }
        }
    }

    root.color = COLOR.BLACK;
    return true;
}

验证是否为红黑树

中序遍历

红黑树是二叉搜索树，所以应该满足中序遍历结果是一个从小到大的有序序列

public void inorder(RBTreeNode root){
    if (root == null){
        return;
    }
    inorder(root.left);
    System.out.println(root.val);
    inorder(root.right);
}

判断根节点的颜色

如果是空树，我们认为这棵树是红黑树，不是空树的话需要判断这棵树的根节点是否为黑色，如果不是黑色，说明这棵树不是红黑树

if(root == null){
    //空树是红黑树
    return true;
}

if(root.color != COLOR.BLACK){
    System.out.println("根节点不是黑色");
    return false;
}

判断红色节点的孩子节点是否为红色节点

通过另外单写一个方法，可以实现递归查询每一个树的左子树是否满足和右子树是否满足

首先判断传入的节点是否为空，如果是空则返回true

然后判断这个节点是否为红色节点，如果是，则判断他的孩子节点有没有红色的，如果有，说明不满足性质——红色节点的孩子节点不能是红色的，那么就直接返回false

然后去分别判断root的左子树和root的右子树是否满足条件，必须都满足才能返回true，因此是&&的关系

private  boolean checkRedColor(RBTreeNode root){
    if(root == null){
        return true;
    }

    if (root.color == COLOR.RED){
        RBTreeNode parent = root.parent;
        if(parent.color == COLOR.RED){
            System.out.println("红色节点的孩子节点还是红色节点");
            return false;
        }
    }

    return checkRedColor(root.left) && checkRedColor(root.right);
}

判断每条路径的黑色节点总数是否相等

先求出红黑树的某一条路径的黑色节点个数，然后拿这个个数去和其他的路径进行比较

int blackNum = 0;
RBTreeNode cur = root;
while(cur != null){
    if(cur.color == COLOR.BLACK){
        blackNum++;
    }
    cur = cur.left;
}

单写一个判断黑色节点总数的方法，方便我们递归

这里的参数分别有如下的含义：pathBlackNum代表递归到现在时的黑色节点的总个数，而blackNum则是我们计算好了的某一条路径上的黑色节点的总个数

首先判断传入的节点是否为空，如果是空则返回true

然后判断传入的节点是否为黑色的，如果是黑色的，我们就需要让pathBlackNum++，代表这个路径上又多了一个黑色的节点

接着看传入的节点的左右孩子节点是否为空，如果都为空，说明当前传入的节点是叶子节点，那么我们就可以去看当前路径的黑色节点总数pathBlackNum和之前计算的路径中黑色节点个数blackNum是否相等，如果不相等，说明这个路径的黑色节点个数和别的不一致，那么就不是红黑树

然后，分别递归去看左子树的黑色节点个数和右子树的黑色节点个数是否符合要求

private boolean checkBlackNum(RBTreeNode root, int pathBlackNum, int blackNum) {
    if (root == null){
        return true;
    }

    if (root.color == COLOR.BLACK){
        pathBlackNum++;
    }

    if(root.left == null && root.right == null){
        if(pathBlackNum != blackNum){
            System.out.println("某条路径上的黑色节点总数和其他路径的黑色节点总数不一致");
            return false;
        }
    }

    return checkBlackNum(root.left, pathBlackNum, blackNum)
            && checkBlackNum(root.right, pathBlackNum, blackNum);
}

完整检查是否为红黑树代码

public boolean isRBTree() {
    if(root == null){
        //空树是红黑树
        return true;
    }

    if(root.color != COLOR.BLACK){
        System.out.println("根节点不是黑色");
        return false;
    }

    //计算最红黑树的最左面路径的黑色节点个数
    int blackNum = 0;
    RBTreeNode cur = root;
    while(cur != null){
        if(cur.color == COLOR.BLACK){
            blackNum++;
        }
        cur = cur.left;
    }

    //检查是否有红色节点的孩子节点也是红色节点，检查是否某条路径上的黑色节点总数和其他路径的黑色节点总数不一致
    return checkRedColor(root) && checkBlackNum(root,0, blackNum);
}

主函数调用

package rbTree;

public class Test {
    public static void main(String[] args) {
        //int[] array = {16,3,7,11,9,26,18,14,15};
        int[] array = {4,2,6,1,3,5,15,7,16,14};
        RBTree rbTree = new RBTree();
        for (int i = 0; i < array.length; i++) {
            rbTree.insert(array[i]);
        }

        rbTree.inorder(rbTree.root);
        System.out.println(rbTree.isRBTree());
    }
}