【图像处理】FAST、BRIEF、ORB算法原理

整理FAST、BRIEF、ORB算法的原理。

FAST算法

一、FAST简介

FAST（features from accelerated segment test）是一种角点检测算法，可以用于提取特征点，后来也长用于目标跟踪等计算机视觉任务中。FAST角点检测算法最初由 Edward Rosten 和 Tom Drummond 提出，并于2006年正式发表。如名字所示，FAST算法最大的优势就是计算效率，相比于其他特征检测算法（例如SIFT、SUSAN、Harris和DOG等）更加快速。此外，通过应用机器学习方法，FAST可以在计算时间和资源等方面得到进一步的性能提升。由于快速高效的性能，FAST角点检测算法非常适合实时视频处理应用。

二、FAST算法原理

FAST角点检测算法主要考虑像素点邻域的圆形窗口上的16个像素。如下图所示，作者认为，以像素 p 为中心的周围圆环上的16个像素中，如果有连续 n 个像素点的灰度值都比 p 点的灰度值大或都小，则认为 p 是一个角点。

实际上，在比较像素灰度值时，需要加上一个阈值 t。
$S_{p \rightarrow x} = \begin{cases} d, \quad I_{p \rightarrow x} \leq I_{p}-t \quad (darker)\\ s, \quad I_{p}-t < I_{p \rightarrow x} < I_{p}+t \quad (similar)\\ b, \quad I_{p}-t \leq I_{p \rightarrow x} \quad (brighter) \end{cases}\\ 其中，p \rightarrow x\ 表示像素点p周围圆环上的像素点x，(x=1,2,...,16),S_{p \rightarrow x}表示p点灰度对应的区间类别$
也就是说，如果 p 点邻域有连续 n 个点比较的结果为 $S_{p \rightarrow x} = d \ 或 \ b$ ，则认为 p 是角点。一般情况下， n 取12，称为FAST-12；实际中， n=9 的效果会更好一些。

由上面的分析可知，对于图像上的每个像素点，我们都需要遍历其邻域圆环上的16个像素点。实际的运用中，我们可以采用一种更加高效的检测方法，只需要检测第1，9，5和13四个位置的像素，就可以剔除掉一大部分非角点的像素。具体的做法是：

先检测第1和第9个像素，如果它们都与中心像素点 p 相似（即 $S_{p \rightarrow x} = s$ ），说明点 p 不是角点；否则继续检测第5和第13个像素点，如果这4个像素点中至少有3个像素点不相似（ $S_{p \rightarrow x} = d \ 或 \ b$ ），则可以认为点 p 是角点，否则 p 肯定不是角点。

如果你已经理清楚了上面的4点检测思想，可以跳过下面这段补充理解：

首先，上面的4点检测方法是针对 n=12 而言的，对于 n=9 不适用
另外，对于 n=12 的情况，即需要保证连续12个像素点的灰度值均大于或小于中心像素点才是角点。因此，如果第1和第9个像素都与中心像素相似，则无论如何都不可能保证连续12个像素满足角点的条件，即此时的p不可能是角点；
若继续考虑第5和第13个像素（即1，5，9，13一起考虑），如果不能满足至少3个像素与 p 不相似，显然 p 就无法保证连续12个点与它不相似的条件， p 就肯定不是角点；
否则，可以认为 p 是一个角点。事实上这是一种粗略的角点筛选，检测这4个点只能保证剔除不是角点的像素，还无法保证这个点就是角点。如果想要提高检测精度，可以继续检测完全部的16个像素，毕竟在剔除大部分非角点像素后，即使再检测完16个像素的计算量也会比原来少了很多。

上述方法的缺点：

当 n<12 时，上述的高效检测方法不再适用
检测的效率依赖于选择的4个点的检测顺序和角点附近的分布
多个特征点检测的结果可能彼此相邻（可以通过非极大值抑制来解决）

三、非极大值抑制

计算每个特征点的score（定义为中心像素与其周围16个像素点灰度值的差的绝对值之和）
对于相邻的特征点，比较它们的score值，对score值较小的特征点会被删除

四、FAST算法总结

FAST角点检测算法最大的特点就是速度快
FAST检测角点的数量依赖于一个 t 值，需要人为设置， t 越大，检测到的角点数量越少
受图像噪声影响大
FAST没有尺度不变性和旋转不变性

BRIEF算法

一、BRIEF简介

BRIEF（Binary Robust Independent Elementary Features）是一种特征描述子，而不是一种特征提取算法，因此不同于Harris、FAST、SIFT、SURF等特征检测算法。BRIEF算法由Michael Calonder等人在ECCV2010上上提出，采用了二进制串来描述特征，相比于SIFT的浮点型描述子而言，BRIEF描述子生成的速度更快，且其特征匹配速度也大大提升。

二、BRIEF算法原理

BRIEF算法的主要思想是，在特征点邻域的 s×s 窗口内随机选取 n 个点对，通过比较这些点对来生成一个二进制串作为该特征点的特征描述子。

注意：BRIEF只是特征描述子，特征点的提取要靠别的特征提取算法来完成，如FAST等。

具体的步骤：

先对整幅图像提取特征点
为了减少噪声影响，对图像进行高斯滤波（因为BRIEF随机选取点对，对噪声比较敏感）
对于某个特征点，在其 s×s 的邻域内随机选取一个点对，比较两个点的大小：
$T(x,y)=\begin{cases} 1, \quad if\ p(x)<p(y)\\ 0. \quad otherwise\end{cases}\\ 其中，p(x)、p(y)分别为随机点对(x,y)的灰度值$
重复第3步 n 次，将 n 次比较的结果组合一个二进制串作为该特征点的特征描述子。一般 n 取128，256或512。

三、随机点对的选取

假设在特征点 s×s 的邻域内随机选取的某个点对为（x，y），作者提供了5种方法：

x和y都采用均匀分布采样
x和y都采用 $(0,\frac{s^{2}}{25})$ 的高斯分布各向同性采样
x服从高斯分布 $(0,\frac{s^{2}}{25})$ ，y服从高斯分布 $(0,\frac{s^{2}}{100})$
x和y均在空间量化极坐标下的离散位置随机采样
x固定在（0，0）位置，y在邻域内随机选取

这里写图片描述

四、BRIEF特征匹配

因为是很简单的二进制串，BRIEF算法直接采用汉明距离来匹配两个特征点。（注意：汉明距离是指两个二进制串中对应位置不同元素的个数）

经过大量实验数据测试，对于 n=256 即256维的BRIEF特征描述子，不匹配特征点的描述子的汉明距离在128左右，匹配点对描述子的汉明距离则远小于128。

因此，可以通过以下方法来判断特征点是否匹配：

两个特征点的二进制串对应位置相同元素个数小于128的，一定不配对；
一幅图上特征点与另一幅图上二进制串对应位置相同元素的个数最多的特征点配成一对。

五、BRIEF优缺点

优点：算法简单，时间和空间复杂度较低，特征匹配快

缺点：容易受噪声影响，不具有尺度不变性和旋转不变性

ORB算法

一、ORB简介

ORB（Oriented Fast and Rotated Brief）是一种特征提取算法，它将FAST和BRIEF算法结合起来并做了改进。ORB算法的速度非常快，并且解决了BRIEF描述子不具备旋转不变性的问题，ORB算法是最常见的传统特征检测算法之一。

二、ORB算法原理

ORB算法的核心就是，使用FAST算法进行特征检测，然后使用BRIEF算法来进行特征描述。

当然，如果ORB算法就仅仅到此为止，那就没什么特点了，所以它在此基础上做了一些改进。由前面的介绍知道，FAST和BRIEF算法并没有解决图像旋转不变性和尺度不变性的问题。ORB算法其实也没有解决尺度不变性的问题，但是在OpenCV的ORB算法的实现中通过引入图像金字塔来改善了这方面的性能。ORB算法主要解决了BRIEF描述子不具备旋转不变性的问题，具体的做法是：

ORB算法提出了灰度质心法，即计算特征点邻域内所有像素的灰度质心，而通过特征点与质心就可以得到一个向量，将这个向量作为特征点的方向，当图像发生旋转时，通过计算主方向旋转的角度就可以得到图像的旋转变换信息，从而实现旋转不变性。

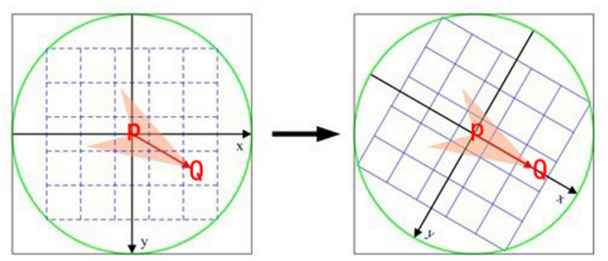
如上图所示，P为特征点，Q为邻域内的灰度质心，向量PQ就是特征点的方向。质心的计算方法如下：
$m_{00}=\sum_{x=-r}^{r}\sum_{y=-r}^{r} I(x,y)\\ m_{10}=\sum_{x=-r}^{r}\sum_{y=-r}^{r} xI(x,y)\\ m_{01}=\sum_{x=-r}^{r}\sum_{y=-r}^{r} yI(x,y)\\ 将上面公式统一起来就是：m_{ij}=\sum_{x=-r}^{r}\sum_{y=-r}^{r} x^{i}y^{j}I(x,y)\\ 其中，I(x,y)是像素点(x,y)的灰度值，i,j只取0或1,r为邻域半径。于是，灰度质心可以表示为：\\ Q=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})\\ 因此，\vec{PQ}就是特征点的方向，特征点的角度表示为：\\ \theta = arctan(m_{01},m_{10})$
Steer BRIEF：

得到了特征点的角度 $\theta$ ，接下来任务就是如何让BRIEF具备旋转不变性了，实现这个目标的方法就是 “Steer BRIEF”。我们知道，BRIEF是通过n个点对来产生一个描述向量的。我们将这n个点对组成一个矩阵S：
$S=\begin{bmatrix} x_{1} & x_{2} &... & x_{2n}\\ y_{1} & y_{2} & ... & y_{2n}\end{bmatrix}$
然后构造一个旋转矩阵，将S旋转到相应的方向上：
$S_{\theta} = R_{\theta}S\\ 其中，R_{\theta}为旋转矩阵：R_{\theta}=\begin{bmatrix} cos\theta & sin\theta\\ -sin\theta & cos\theta\end{bmatrix}$
然后就可以用 $S_{\theta}$ 作为校正后的BRIEF描述子了。