LeetCode 198 打家劫舍
题目简析:
不能偷相邻的屋子,求能偷到的最大金额
思路分析:
//由于是相邻的才偷,因此,我们对于最基础的三间 //dp[3] 应该是 Math.max(dp[2],dp[1]+nums[3]) //如果第一间加偷第三间的价值大于偷第二间的 // 那么dp[3] = dp[1]+nums[3] //若不大于,则第三间不偷,保持偷第二间的价值
而另一个疑点就是如何初始化
对于初始化,因为我们从第三间开始判断,那么就要初始化前两间,当只有一间屋子的时候很显然只能偷到屋子里的金额,当有两间屋子的时候,偷的金额那就是,两间里金额大的
dp[0] = nums[0]; dp[1] = Math.max(nums[0],nums[1]);
public int rob(int[] nums) {
//dp[i]:偷到第i间房能偷到的最高金额
int len = nums.length;
if(len == 0)return 0;
if(len == 1)return nums[0];
//这里不需要再+1
int []dp = new int[len];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
//因此我们直接从第三间开始判断
for (int i = 2; i < len; i++) {
dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
}
return dp[len-1];
}状态压缩版:其实只需要三个变量,而代码思路是一样的
class Solution {
public int rob(int[] nums) {
int pre1 = 0, pre2 = 0;
if (nums.length == 1) {
return nums[0];
}
pre2 = nums[0];
pre1 = Math.max(nums[0], nums[1]);
for (int i = 2; i < nums.length; i++) {
int cur = Math.max(pre1, pre2 + nums[i]);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
}LeetCode 213打家劫舍II
题目简析:
房屋绕环,即第一间和最后一间相邻,不能偷相邻的屋子条件下,求能偷到的最高金额
思路分析:
如代码随想录下图分析:


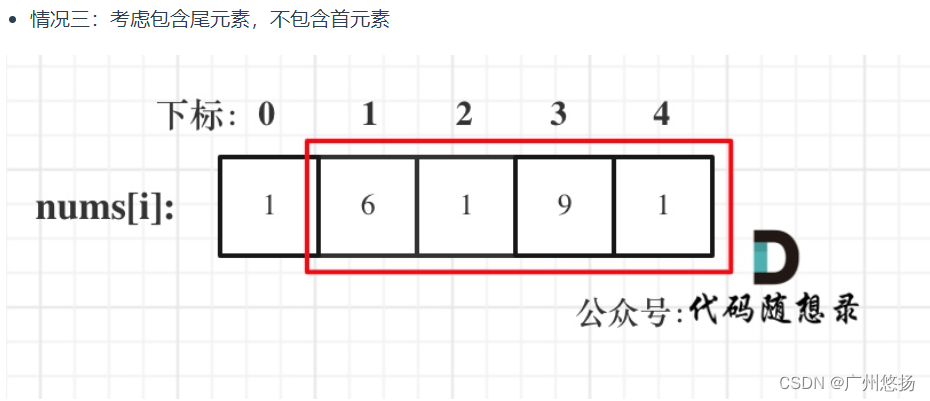
可以看到情况二三的框的交集就是情况一,说明情况二和情况三把情况一包括了,因此我们只需要考虑包含首元素,不包含尾元素,或者考虑包含尾元素,不包含首元素
public int rob(int[] nums) {
//dp[i]:偷到第i间房能偷到的最高金额
int len = nums.length;
if (len == 0) return 0;
if (len == 1) return nums[0];
//而两段代码是一样的,因此我们提取出来
//传入数组区间
int head = rob(nums,0,len-2);
int tail = rob(nums,1,len-1);
return Math.max(head,tail);
}
//把区间传入即可
public int rob(int []nums,int start,int end){
//只有一间屋子的情况
if(start==end)return nums[start];
int []dp = new int[nums.length];
dp[start] = nums[start];
dp[start+1] = Math.max(nums[start],nums[start+1]);
for (int i = start+2; i <= end; i++) {
dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
}
return dp[end];
}LeetCode 337打家劫舍III
题目简析:
树形的房子排列,不能偷相邻的情况下,求偷得的最大金额
思路分析:
涉及到树,首先去想到dfs/bfs,但是做法不涉及到dp
//递归,超时
public int rob(TreeNode root) {
//若父节点没偷,就可以考虑偷左右子节点
if(root==null)return 0;
int money = root.val;
if (root.left != null) {
money += rob(root.left.left) + rob(root.left.right);
}
if (root.right != null) {
money += rob(root.right.left) + rob(root.right.right);
}
//比较当前偷的金额多还是偷子节点的多
return Math.max(money,rob(root.left)+rob(root.right));
}
//记忆化递归----时间不理想,利用Map来作记忆化数组
public int rob(TreeNode root) {
Map<TreeNode, Integer> memo = new HashMap<>();
return robAction(root, memo);
}
int robAction(TreeNode root, Map<TreeNode, Integer> memo) {
if (root == null)
return 0;
//如果已经搜索过了当前结点,就获取偷至当前结点的金额
if (memo.containsKey(root))
return memo.get(root);
int money = root.val;
if (root.left != null) {
money += robAction(root.left.left, memo) + robAction(root.left.right, memo);
}
if (root.right != null) {
money += robAction(root.right.left, memo) + robAction(root.right.right, memo);
}
int res = Math.max(money, robAction(root.left, memo) + robAction(root.right, memo));
memo.put(root, res);
return res;
}由此学习了一种新的解题方法:树形dp
// 3.状态标记递归
// 执行用时:0 ms , 在所有 Java 提交中击败了 100% 的用户
// 不偷:Max(左孩子不偷,左孩子偷) + Max(又孩子不偷,右孩子偷)
// root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +
// Math.max(rob(root.right)[0], rob(root.right)[1])
// 偷:左孩子不偷+ 右孩子不偷 + 当前节点偷
// root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;
public int rob(TreeNode root) {
int[] res = robAction1(root);
return Math.max(res[0], res[1]);
}
int[] robAction1(TreeNode root) {
int res[] = new int[2];
if (root == null)
return res;
int[] left = robAction1(root.left);
int[] right = robAction1(root.right);
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
res[1] = root.val + left[0] + right[0];
return res;
}