✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统
⛄ 内容介绍
元胞自动机(Elementary Cellular Automata)它是一种特殊的网格数学模型,能够很好地反映研究对象的动态特性。因为它对时间、空间、研究对象及其相互作用的描述是谨慎的,元胞自动机模型可以模拟和演化许多复杂的系统。根据一些当地规则,系统在离散时间维度上运行和发展。元胞自动机模型的基本内容是根据测试对象制定适当的移动规则,以便模型可以根据规则进化,然后研究整个系统。元胞自动机模型的发展与数学的发展密切相关。一方面,元胞自动机模型继承了理论自相关结果,如离散数学、模糊数学和图灵机。元胞自动机模型在人工智能、非线性科学、系统科学等领域的基本研究思路是自下而上研究系统元素之间的相互作用,开发非常复杂的模型。
元胞自动机模型由四个部分组成:元胞,元胞空间,元胞邻居和元胞规则,如图2.1所示。

图2.1 元胞自动机构成
1.元胞
如同细胞,是元胞自动机的最小单元。它是元胞自动机模型中最小的单元。细胞存在于离散的欧几里得网络中。根据不同的测试对象,网格可以是一维、二维或多维的,每个单元格都独立于自身,并具有自己的属性。
2.元胞空间
元胞空间就是元胞所在的空间集合。
1)元胞空间的几何划分
从理论上讲,元胞空间的维数没有限制,它可以根据测试对象的复杂性进行定制。目前,对元胞自动机模型的研究大多是一维和二维的,元胞自动机模型的一维模型很简单,只有一种划分方法;元胞自动机模型的尺寸越高,其空间网格就越划分。二维元胞自动机模型的空间结构可以根据不同的平面图形划分为网格,以下三种类型很常见,如图2.2所示。

图2.2 元胞自动机的三种网格
这三个规则的单元划点对建模者有其优点和缺点,三角形网格的优点是相邻网格的数量最少。缺点是很难用计算机语言直接描述它,必须通过转换网格来表示,方形网格的优点是它简单,非常适合演示。缺点是它不能很好地模拟各向同性现象。六边形网格的优点是它可以更好地模拟各向同性现象,并且模型更自然和逼真。
2)元胞边界条件
模拟元胞自动机的运动时,有必要注意移动元胞自动机模型的限制,因为它不能支持无限网格。当然,边界细胞不像内部细胞那样有邻居。可以在极端条件下扩展小区邻居以确定极端条件下的小区移动。最常用的边界条件是周期性(或周期性)边界条件,元胞自动机模型是包含在环拓扑中的虚拟网格。在二维网络中,这意味着左右连接,上下连接,通过预先分配虚拟单元来设置边界,绝热边界是虚拟单元和真实单元之间的值,映射边界是将虚拟单元格中实际单元格周围的单元格值映射,四个边界条件如图2.3所示。在实际应用中,尤其是当单元结构大于二维时,这些边界条件可以相互组合.
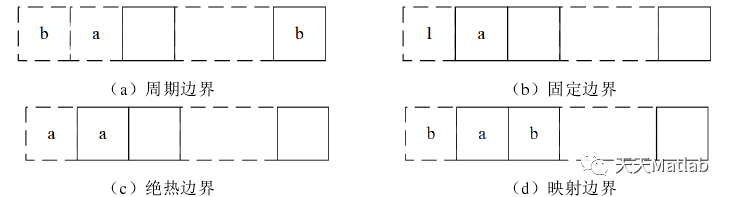
图2.3 一维元胞自动机的四种边界条件
3)元胞构建
元胞构建就是在某一时刻内,整个元胞空间内所有元胞的形态。在正常情况下,可以将其视为多维整数矩阵。
3.元胞邻居
为了使元胞自动机动态演化,必须有进化的规则。这些规则是在本地空间范围内定义的。小区的状态是动态的,由前一时间小区的状态和前一时间相邻小区的状态决定,小区的邻居必须首先靠近小区,然后给出半径r的值。以小区为中心、半径r为半径的圆中的所有小区都是小区的邻居,对于高维移动自动售货机,邻里关系与空间结构密切相关。冯·诺伊曼型、摩尔型和摩尔扩展型(von1-Veumann型、摩尔类型和摩尔扩展类型)最常用于二维元胞自动机模型。物理系统的大多数模拟也基于这三个相邻结构,如图2.4所示,他们的状态组合决定了下一时刻中央元胞的状态。
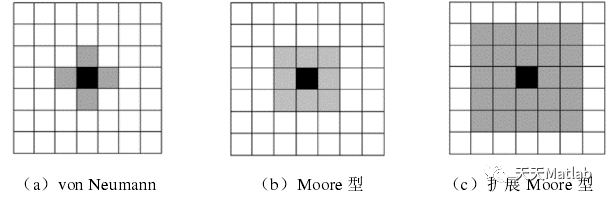
图2.4 二维元胞自动机常用邻居类型
4.元胞规则
状态转移函数是下一个时刻元胞状态的动态函数它由当前状态和与单元相邻的状态确定,该函数在空间和时间上建立了简单而谨慎的局部物理结构,结构本身不会改变,但细胞的状态会改变。常用的规则方法包括Pascal's Triangle规则、HexWolfram's Code规则、Outer Totalistic规则和触发规则。
⛄ 部分代码
function [Dst_S]=Dststspread(Dst_S,ZAM,row,col,p)
%Dst_S灾害因素矩阵;p扩散概率;1
Dst_S1=Dst_S;
[I1 I2]=find(Dst_S==1);
for i=1:length(I1)
a=[I1(i),I2(i)-1;I1(i),I2(i)+1;...
I1(i)-1,I2(i);I1(i)+1,I2(i);...
I1(i)+1,I2(i)-1;I1(i)+1,I2(i)+1;...
I1(i)-1,I2(i)-1;I1(i)-1,I2(i)+1];
% b=ones(8,1);
for j=1:8
if a(j,1)>0&&a(j,1)<=row&&a(j,2)>0&&a(j,2)<=col&&ZAM(a(j,1),a(j,2))==0
if rand<p
Dst_S1(a(j,1),a(j,2))=1;
end
end
end
end
% for i=1:row
% for j=1:col
% if Dst_S(i,j)==1||
[I1 I2]=find(Dst_S==1);
for i=1:length(I1)
a=[I1(i),I2(i)-1;I1(i),I2(i)+1;...
I1(i)-1,I2(i);I1(i)+1,I2(i);...
I1(i)+1,I2(i)-1;I1(i)+1,I2(i)+1;...
I1(i)-1,I2(i)-1;I1(i)-1,I2(i)+1;...
I1(i)+2,I2(i)-2;I1(i)+2,I2(i)-1;I1(i)+2,I2(i);I1(i)+2,I2(i)+1;I1(i)+2,I2(i)+2;...
I1(i)-2,I2(i)-2;I1(i)-2,I2(i)-1;I1(i)-2,I2(i);I1(i)-2,I2(i)+1;I1(i)-2,I2(i)+2;...
I1(i)-1,I2(i)-2;I1(i)-1,I2(i)-1;I1(i)-1,I2(i);I1(i)-1,I2(i)+1;...
I1(i)+1,I2(i)-2;I1(i)+1,I2(i)-1;I1(i)+1,I2(i);I1(i)+1,I2(i)+1];
for j=1:8
if a(j,1)>0&&a(j,1)<=row&&a(j,2)>0&&a(j,2)<=col
Dst_S1(a(j,1),a(j,2))=max(0.5, Dst_S1(a(j,1),a(j,2)));
end
end
for j=9:24
if a(j,1)>0&&a(j,1)<=row&&a(j,2)>0&&a(j,2)<=col
Dst_S1(a(j,1),a(j,2))=max(0.4, Dst_S1(a(j,1),a(j,2)));
end
end
end
Dst_S=Dst_S1;
⛄ 运行结果


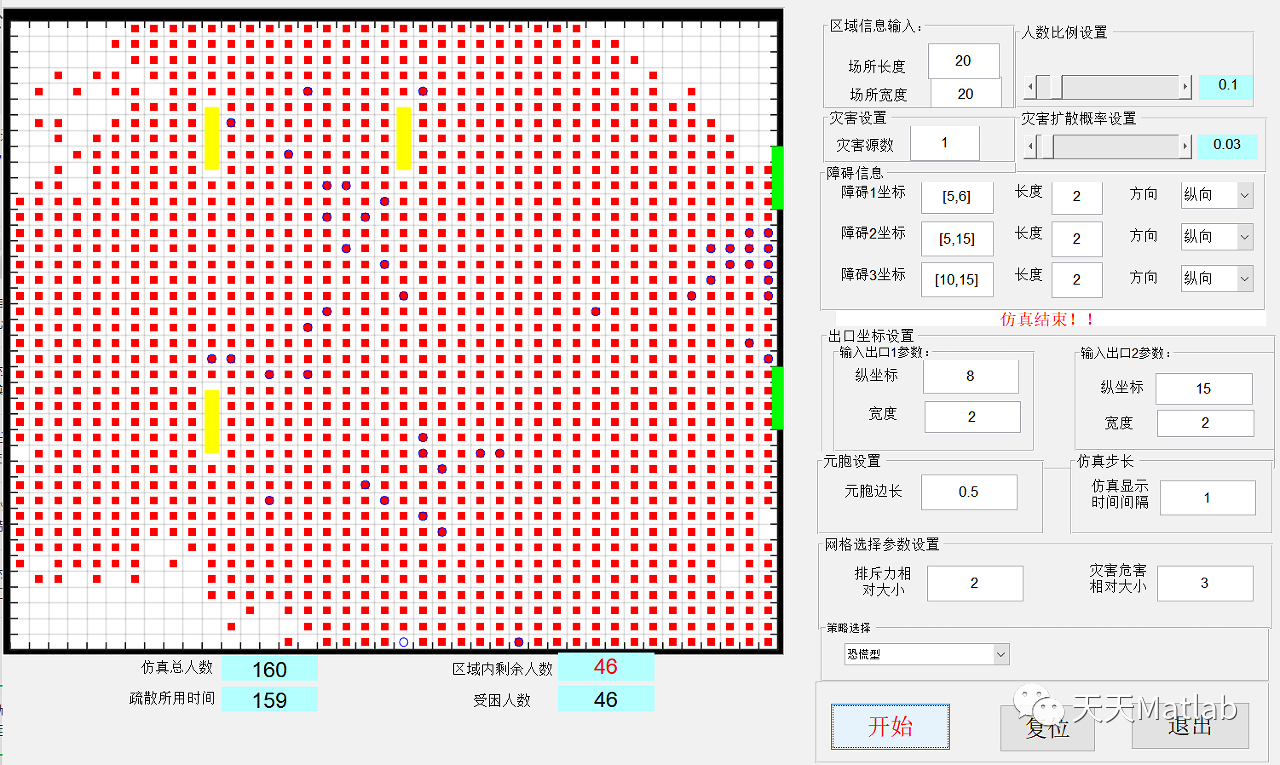
⛄ 参考文献
[1] 梁江涛, 王慧琴. 基于改进蚁群算法的建筑火灾疏散路径规划研究[J]. 系统仿真学报, 2022, 34(5):10.
[2] 李晓明, 刘英浩. 基于BIM技术的建筑消防疏散路径规划研究[J]. 东西南北, 2020(3).
[3] 付强. 融合多源信息的人群疏散路径规划方法及仿真研究[D]. 山东师范大学, 2020.
[4] 程鹏举, 吴楠, 孟凡坤,等. 基于扩展A*算法的火灾逃生路径规划方法及系统[J]. 2021.
[5] 虞鹏飞. 基于动态监测反馈的建筑人员疏散仿真推演技术研究. 中国科学院大学(中国科学院深圳先进技术研究院), 2020.
[6] 赵星, 吉康, 陈吉怀,等. 一种基于非固定路线的往返式公交疏散路径规划方法:, CN111680822A[P]. 2020.
[7] 贾进章, 李雪娇. 基于遗传-蚁群算法的单层建筑火灾疏散路径规划研究[J]. 中国安全生产科学技术, 2020, 16(6):5.
⛄ Matlab代码关注
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料