[JLOI2009]二叉树问题

题目描述

如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度： $4$
宽度： $4$
结点 8 和 6 之间的距离： $8$
结点 7 和 6 之间的距离： $3$

其中宽度表示二叉树上同一层最多的结点个数，节点 $u, v$ 之间的距离表示从 $u$ 到 $v$ 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。

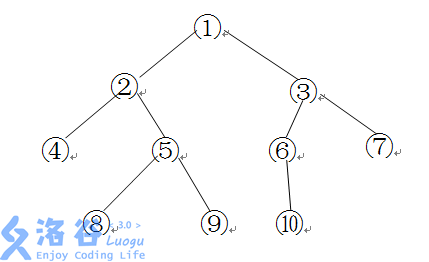
给定一颗以 1 号结点为根的二叉树，请求出其深度、宽度和两个指定节点 $x, y$ 之间的距离。

输入格式

第一行是一个整数，表示树的结点个数 $n$ 。
接下来 $n - 1$ 行，每行两个整数 $u, v$ ，表示树上存在一条连接 $u, v$ 的边。
最后一行有两个整数 $x, y$ ，表示求 $x, y$ 之间的距离。

输出格式

输入三行，每行一个整数，依次表示二叉树的深度、宽度和 $x, y$ 之间的距离。

样例 #1

样例输入 #1

样例输出 #1

4
4
8

提示

对于全部的测试点，保证 $\leq u, v, x, y \leq n \leq 100$ ，且给出的是一棵树。

分析

首先要明白u、v的距离咋算，题目说的也是听含糊，实际就是，从孩子向根的方向走，一条边距离为2；从根向孩子的方向走一条边的距离为1；
树其实就是一种图，没有环、连通；所以求距离问题可以转化为最短路问题，在这里Floyd即可解决；
求树深，可以用dfs，dfs过程和之前的7-53 生化危机有点像，两点之间有边才去向下搜；7-22 图中最深的根，这个题也是dfs求树深，思路差不多，只不过用的是邻接表存储的图，这题用的邻接矩阵；
求树的宽度，用一个cnt数组，记录根经过某个距离所能到达的结点数，cnt的维度表示就是某个距离；cnt数组存的是每个**距离（根到某一点）**下的结点个数，根到 i 有相同距离的点，说明在同一层；直接计算根能到达的点，cnt[a[1][i]]++；

#include<bits/stdc++.h>

using namespace std;
int n, depth, width;
int a[105][105];
int vis[105];
int cnt[205];//根经过某个距离到达的结点数（求宽度用）

//求树深
void dfs(int u, int step) {
    for (int i = 1; i <= n; ++i) {
        if (!vis[i] && a[u][i] != 1000) {
            depth = max(depth, step);
            vis[i] = 1;
            dfs(i, step + 1);
            vis[i] = 0;
        }
    }
}

int main() {
    //初始化
    for (int i = 1; i <= 105; ++i) {
        for (int j = 1; j <= 105; ++j) {
            a[i][j] = 1000;
        }
    }
    //玄学，全局变量还带初始化
    memset(vis, 0, sizeof vis);
    cin >> n;
    int u, v, x, y;
    for (int i = 0; i < n - 1; ++i) {
        cin >> u >> v;
        a[u][v] = 1;//向下
        a[v][u] = 2;//逆行
    }
    cin >> x >> y;

    //1、求深度
    dfs(1, 0);
    cout << depth << endl;

    //2、Floyd求距离，由于统计宽度也待用两点距离，所以放上面
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
            }
        }
    }

    //3、求宽度
    for (int i = 2; i <= n; ++i) {
        cnt[a[1][i]]++;//每一层的节点数(根到i有相同距离的点，说明在同一层)
    }
    for (int i = 1; i <= 205; ++i) {// 树为一条链，最大距离也就100*2
        width = max(width, cnt[i]);
    }
    cout << width << endl;
    cout << a[x][y];
    return 0;
}