1.问题描述

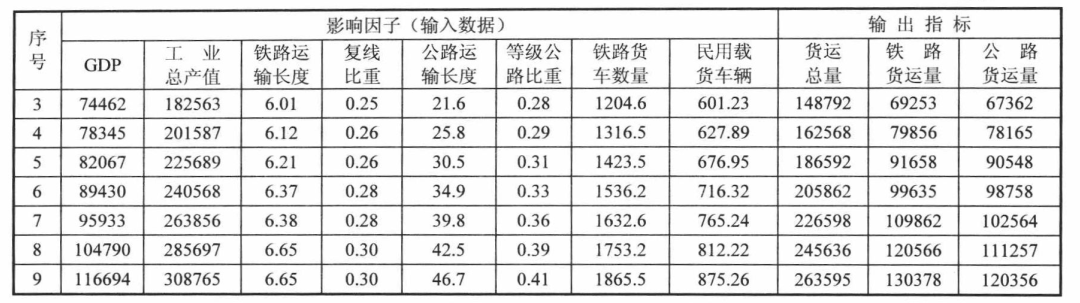
某运输系统连续9年货运量的有关数据如表2-10所示。根据对关于货运量影响因素的分析，这里分别取国内生产总值GDP、工业总产值、铁路运输线路长度、复线里程比重、公路运输线路长度、等级公路比重、铁路货车数量和民用载货车辆数量等8项指标作为影响货运量的因素，以货运总量、铁路货运量和公路货运量作为货运量的输出指标。根据这些资料，可利用神经网络对运输系统进行货运量预测。

1.1问题剖析

①可以看到这里给出了样本集，而且是已知输入对应目标输出的样本集，所以可以理解为有教师的学习方式做训练和预测。为了验证我么学习好的网络，所以这里将前8组数据作为训练样本集，最后一组数据作为测试样本集。

②由于系统的实际输入/输出数据常常不在[0,1]之间，而神经网络一般要求在[0,1]之间，所以需要在训练神经网络前进行归一化处理。最后对于输出要进行反归一化处理，常见的归一化处理方式为：

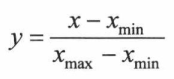
所以对应的反归一化为：

也可以使用matlab提供的库函数进行归一化和反归一化：

注：ps为与归一化有关的值，在归一化时可以省略，但是反归一化时不可省略。

③由于使用matlab训练常常借助其库函数能节省很多时间，所以这里先介绍BP网络的重要函数和基本功能：

神经网络通用函数：

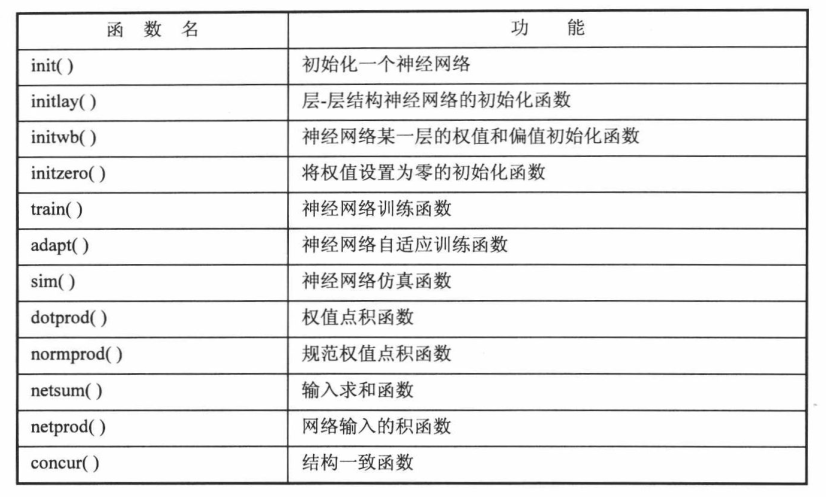
BP神经网络函数：

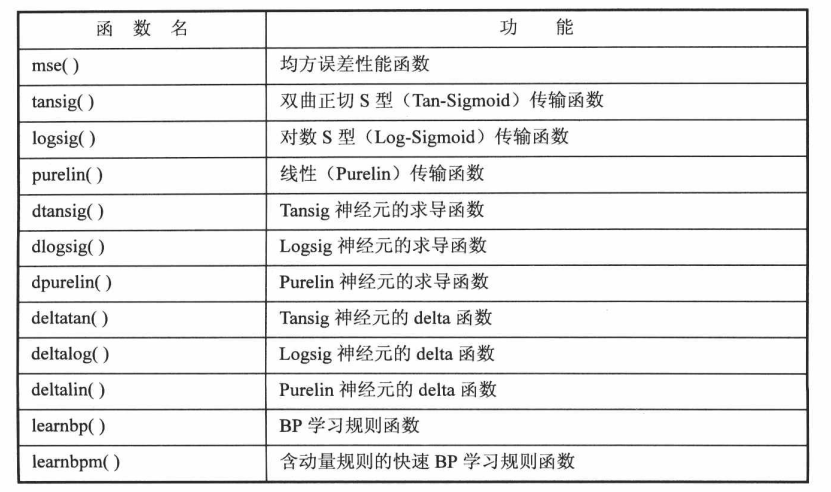
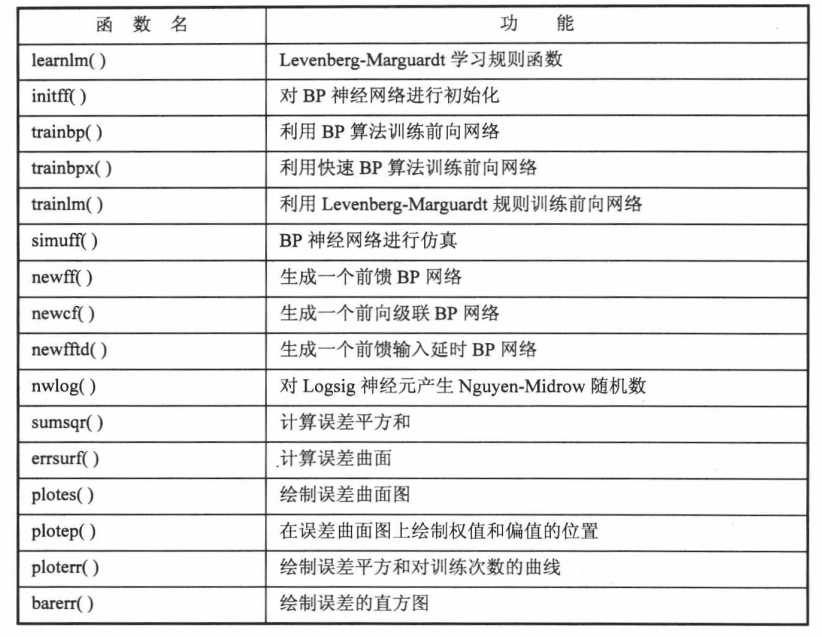
这里主要对下面即将用上的建立网络函数newff、训练神经网络函数train做一个详细的介绍：

2.实现程序

%%①确定样本集
%X=[GPD，工业总产值，铁路运输长度，复线比重，公路运输长度，等级公路比重，铁路货车数量，民用载货车辆]
x = [58478,135185,5.46,0.23,16.5,0.21,1005.3,585.44;
    67884,152369,5.46,0.27,18.7,0.26,1105.6,575.03;
    74462,182563,6.01,0.25,21.6,0.28,1204.6,601.23;
    78345,201587,6.12,0.26,25.8,0.29,1316.5,627.89;
    82067,225689,6.21,0.26,30.5,0.31,1423.5,676.95;
    89430,240568,6.37,0.28,34.9,0.33,1536.2,716.32;
    95933,263856,6.38,0.28,39.8,0.36,1632.6,765.24;
    104790,285697,6.65,0.30,42.5,0.39,1753.2,812.22;
    116694,308765,6.65,0.30,46.7,0.41,1865.5,857.26]';
%目标输出T=[货运总量，铁路货运量，公路货运量]
t = [102569,52365,46251;124587,60821,56245;148792,69253,67362;
    162568,79856,78165;186592,91658,90548;205862,99635,98758;
    226598,109862,102564;245636,120566,111257;263595,130378,120356]';
%%②归一化处理
a = [1 2 3 4 5 6 7 8];X = x;T = t;
for i = 1:8  %对样本输入前8组数据进行归一化处理
    X(a(i),:) = (x(a(i),:)-min(x(a(i),:)))/(max(x(a(i),:))-min(x(a(i),:)));
end
for i = 1:3  %对样本输入前8组数据进行归一化处理
    T(a(i),:) = (t(a(i),:)-min(t(a(i),:)))/(max(t(a(i),:))-min(t(a(i),:)));%(某行数据-该行数据最小值)/(该行数据最大值-该行数据最小值)
end
% [X,ps] = mapminmax(x(1:8,:),0,1);X1 = mapminmax('reverse',X,ps);使用库函数归一化
% [T,ps] = mapminmax(t(1:3,:),0,1);
%%③网络设计和训练
X1 = X(:,1:8);T1 = T(:,1:8);%某一列的所有数据作为一组训练输入
%隐藏层神经元个数q=2*M(输入层神经元8个)+1=17，隐藏层神经元传递函数采用tansig双曲正切对称s函数
%输出层神经元传递函数采用logsig s函数，满足网络输出在[0,1]之间
net = newff(minmax(X1),[17,3],{'tansig','logsig'},'trainlm');
net.trainParam.epochs = 1000;%设定训练次数
net.trainParam.goal = 0.0001;%目标最小均方值
LP.lr = 0.1;%学习率
net = train(net,X1,T1);%训练
y1 = sim(net,X1)%输入1-8组数据，训练得到的1-8组输入数据对应的实际输出

2.1运行结果

将原始输入数据作为训练好的网络输入得到的实际输出y1(归一化下)如下：

目标输出(归一化下)如下：

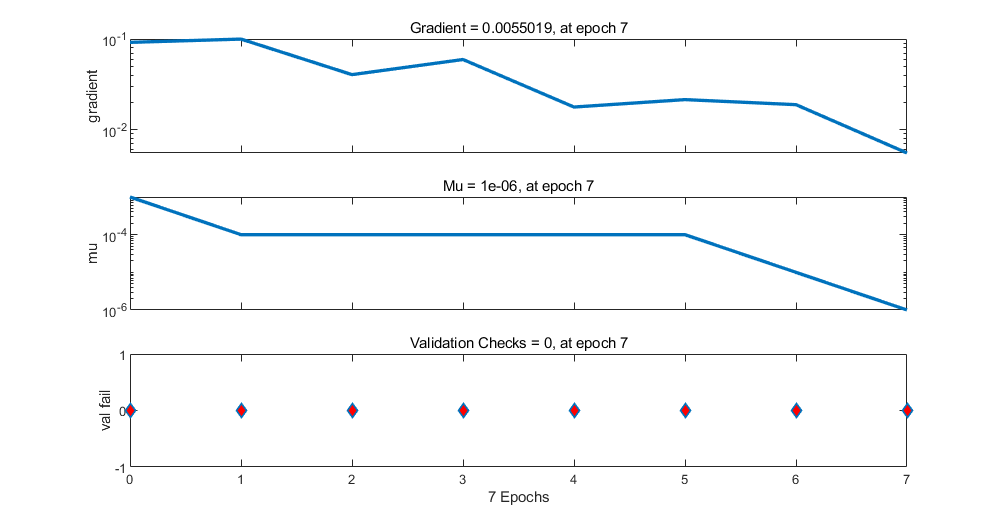
目标函数(均方差)迭代曲线：

在运行前，提前打开nntool工具箱还可以查看训练状态和网络结果等等信息，当然也可以用命令查看(这里不做叙述)：

2.3总结

①通过实际输出y1和目标输出T对比可以看到，训练得到的实际输出能够很接近目标输出；

②通过查看误差迭代曲线可以看到，经过7代便可以达到我们设定的0.0001(即1e-4)的误差目标最小值。

注：由于是学习训练，所以每次实际输出和迭代停止次数是不同的，但差异不大。

3.预测

利用完前8组数据做学习训练后得到了我们的BP网络，现在可以将第9组数据作为测试数据，其测试程序如下：

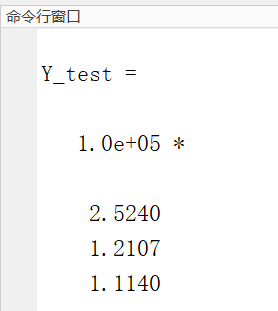
X_test = X(:,9);%表中的第9组输入数据
y_test = sim(net,X_test);%归一化的实际输出
for i = 1:1:3%使用for循环反归一化
    Y_test(i,:) = y_test(i,:)*(max(t(i,:))-min(t(i,:))+min(t(i,:)))
end