opencv基础49-图像轮廓02-矩特征cv2.moments()-＞（形状分析、物体检测、图像识别、匹配）

矩特征（Moments Features）是用于图像分析和模式识别的一种特征表示方法，用来描述图像的形状、几何特征和统计信息。矩特征可以用于识别图像中的对象、检测形状以及进行图像分类等任务。

矩特征通过计算图像像素的高阶矩来提取特征。这些矩可以表示图像的中心、尺度、旋转和形状等属性。以下是一些常见的图像矩特征：

零阶矩（Zeroth-Order Moments）：描述图像的总体亮度或面积，通常表示为图像的像素数。
一阶矩（First-Order Moments）：描述图像的质心、平均位置和分布。它们用于计算图像的中心位置。
中心矩（Central Moments）：描述图像区域相对于质心的分布。中心矩能够捕获图像的旋转和平移特性。
标准化矩（Normalized Moments）：将矩标准化以获得尺度和旋转不变性。标准化矩可以用于匹配和识别。
**Hu不变矩（Hu Moments）：**基于七个基本矩构建，具有旋转、平移和尺度不变性。Hu不变矩用于图像匹配和模式识别。

什么是图像的质心？

图像的质心（Centroid）是一个表示图像几何中心的概念。在二维平面上，图像的质心是指图像中所有像素的平均位置，即图像的重心或几何中心。

对于二值图像（黑白图像），质心可以通过以下方式计算：

将图像中的每个像素视为一个点，其坐标为 (x, y)。对于每个像素点，计算其 x 坐标的总和和 y 坐标的总和。
用总和除以图像中像素的总数，得到 x 和 y 坐标的平均值，即为质心的坐标。
质心的坐标表示图像在水平和垂直方向上的平均位置。在实际应用中，质心通常被用于描述图像的位置信息，例如目标的位置、形状的中心等。对于多通道彩色图像，可以分别计算每个通道的质心。

矩特征应用场景

矩特征在图像处理和模式识别领域有许多应用场景，可以用于描述图像的形状、几何属性和分布情况。以下是一些常见的矩特征应用场景：

物体识别和分类：矩特征可以用于提取图像中物体的形状和几何特征，从而进行物体的识别和分类。通过比较矩特征，可以判断物体是否属于某个类别。
目标检测：在计算机视觉中，目标检测是指在图像中找到特定物体的位置。矩特征可以用于检测物体的形状和轮廓，从而帮助确定物体的位置。
图像匹配：矩特征可以用于图像的匹配和对准，通过比较两幅图像的矩特征，可以找到它们之间的相似性和变换关系。
图像压缩和编码：矩特征可以用于图像的压缩和编码，通过提取图像的主要几何信息，可以减少图像数据的存储空间。
图像分割：图像分割是将图像分成不同的区域，矩特征可以用于描述不同区域的形状和几何属性，从而帮助分割图像。
医学图像分析：在医学领域，矩特征可以用于分析医学图像中的组织、器官和病变，从而提取形状和几何特征。
指纹识别：矩特征可以用于指纹识别，通过提取指纹图像的几何特征，实现指纹的识别和比对。
遥感图像分析：在遥感图像中，矩特征可以用于提取地物的形状和分布，从而实现土地利用、环境监测等应用。

矩的计算：moments函数

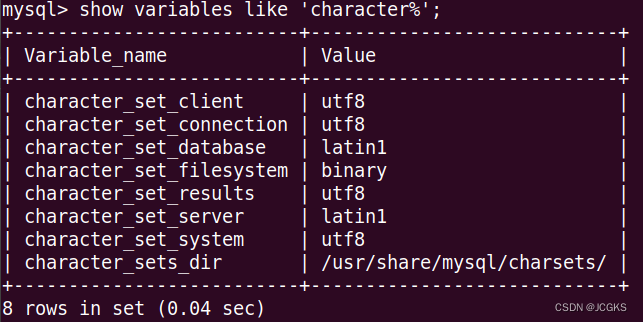
OpenCV 提供了函数 cv2.moments()来获取图像的 moments 特征。通常情况下，我们将使用函数 cv2.moments()获取的轮廓特征称为“轮廓矩”。轮廓矩描述了一个轮廓的重要特征，使用轮廓矩可以方便地比较两个轮廓。

函数 cv2.moments()的语法格式为：

retval = cv2.moments( array[, binaryImage] )

array：可以是点集，也可以是灰度图像或者二值图像。当 array 是点集时，函数会把这些点集当成轮廓中的顶点，把整个点集作为一条轮廓，而不是把它们当成独立的点来看待。
binaryImage：该参数为 True 时，array 内所有的非零值都被处理为 1。该参数仅在参数array 为图像时有效。

该函数的返回值 retval 是矩特征，主要包括：

（1）空间矩

零阶矩：m00
一阶矩：m10, m01
二阶矩：m20, m11, m02
三阶矩：m30, m21, m12, m03
（2）中心矩
二阶中心矩：mu20, mu11, mu02
三阶中心矩：mu30, mu21, mu12, mu03
（3）归一化中心矩
二阶 Hu 矩：nu20, nu11, nu02
三阶 Hu 矩：nu30, nu21, nu12, nu03

上述矩都是根据公式计算得到的，大多数矩比较抽象。但是很明显，如果两个轮廓的矩一致，那么这两个轮廓就是一致的。虽然大多数矩都是通过数学公式计算得到的抽象特征，但是
零阶矩“m00”的含义比较直观，它表示一个轮廓的面积。

矩特征函数 cv2.moments()所返回的特征值，能够用来比较两个轮廓是否相似。例如，有两个轮廓，不管它们出现在图像的哪个位置，我们都可以通过函数 cv2.moments()的 m00 矩判断其面积是否一致。

在位置发生变化时，虽然轮廓的面积、周长等特征不变，但是更高阶的特征会随着位置的变化而发生变化。在很多情况下，我们希望比较不同位置的两个对象的一致性。解决这一问题的方法是引入中心矩。中心矩通过减去均值而获取平移不变性，因而能够比较不同位置的两个对象是否一致。很明显，中心矩具有的平移不变性，使它能够忽略两个对象的位置关系，帮助我们比较不同位置上两个对象的一致性。

除了考虑平移不变性外，我们还会考虑经过缩放后大小不一致的对象的一致性。也就是说，我们希望图像在缩放前后能够拥有一个稳定的特征值。也就是说，让图像在缩放前后具有同样的特征值。显然，中心矩不具有这个属性。例如，两个形状一致、大小不一的对象，其中心矩是有差异的。

归一化中心矩通过除以物体总尺寸而获得缩放不变性。它通过上述计算提取对象的归一化中心矩属性值，该属性值不仅具有平移不变性，还具有缩放不变性。

在 OpenCV 中，函数 cv2.moments()会同时计算上述空间矩、中心矩和归一化中心距。

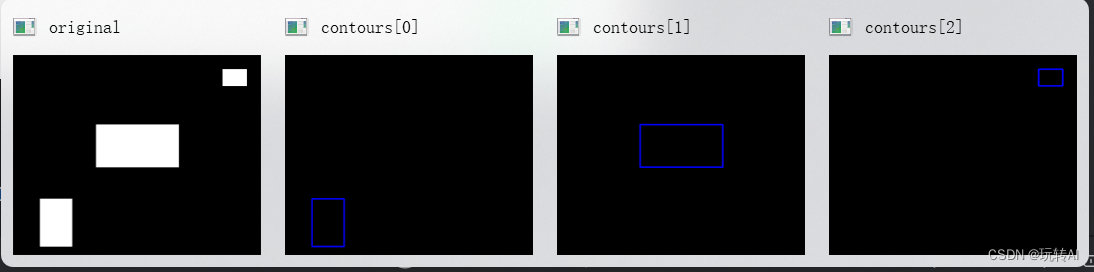
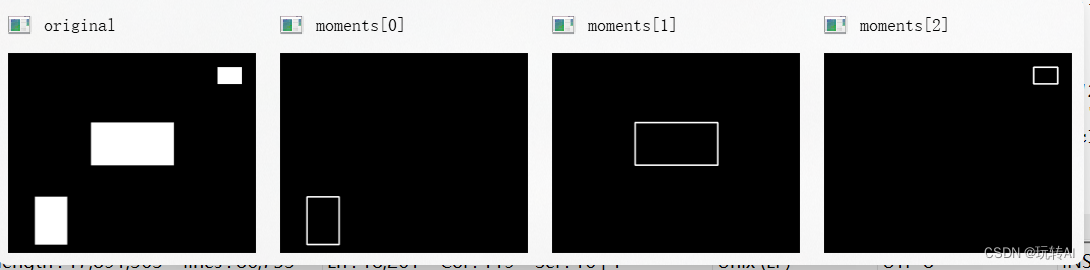
示例：使用函数 cv2.moments()提取一幅图像的特征。

代码如下：


import cv2
import numpy as np
o = cv2.imread('moments.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
 cv2.CHAIN_APPROX_SIMPLE)
n=len(contours)
contoursImg=[]
for i in range(n):
 temp=np.zeros(o.shape,np.uint8)
 contoursImg.append(temp)
 contoursImg[i]=cv2.drawContours(contoursImg[i],contours,i,255,3)
 cv2.imshow("contours[" + str(i)+"]",contoursImg[i])
print("观察各个轮廓的矩（moments）:")
for i in range(n):
 print("轮廓"+str(i)+"的矩:\n",cv2.moments(contours[i]))
print("观察各个轮廓的面积:")
for i in range(n):
 print("轮廓"+str(i)+"的面积:%d" %cv2.moments(contours[i])['m00'])
cv2.waitKey()
cv2.destroyAllWindows()

本例中，首先使用函数 cv2.moments()提取各个轮廓的特征；接下来，通过语句
cv2.moments(contours[i])[‘m00’])提取各个轮廓矩的面积信息。

运行结果如下：

观察各个轮廓的矩（moments）:
轮廓0的矩:
 {'m00': 14900.0, 'm10': 1996600.0, 'm01': 7800150.0, 'm20': 279961066.6666666, 'm11': 1045220100.0, 'm02': 4110944766.6666665, 'm30': 40842449600.0, 'm21': 146559618400.0, 'm12': 550866598733.3334, 'm03': 2180941440375.0, 'mu20': 12416666.666666627, 'mu11': 0.0, 'mu02': 27566241.666666508, 'mu30': 1.52587890625e-05, 'mu21': 2.09808349609375e-05, 'mu12': 6.198883056640625e-05, 'mu03': 0.000244140625, 'nu20': 0.05592841163310942, 'nu11': 0.0, 'nu02': 0.12416666666666591, 'nu30': 5.630596400372416e-16, 'nu21': 7.742070050512072e-16, 'nu12': 2.2874297876512943e-15, 'nu03': 9.008954240595866e-15}
轮廓1的矩:
 {'m00': 34314.0, 'm10': 13313832.0, 'm01': 9728019.0, 'm20': 5356106574.0, 'm11': 3774471372.0, 'm02': 2808475082.0, 'm30': 2225873002920.0, 'm21': 1518456213729.0, 'm12': 1089688331816.0, 'm03': 824882507095.5, 'mu20': 190339758.0, 'mu11': 0.0, 'mu02': 50581695.5, 'mu30': 0.0, 'mu21': 0.0, 'mu12': 0.0, 'mu03': 0.0, 'nu20': 0.16165413533834588, 'nu11': 0.0, 'nu02': 0.042958656330749356, 'nu30': 0.0, 'nu21': 0.0, 'nu12': 0.0, 'nu03': 0.0}
轮廓2的矩:
 {'m00': 3900.0, 'm10': 2696850.0, 'm01': 273000.0, 'm20': 1866699900.0, 'm11': 188779500.0, 'm02': 19988800.0, 'm30': 1293351277725.0, 'm21': 130668993000.0, 'm12': 13822255200.0, 'm03': 1522248000.0, 'mu20': 1828125.0, 'mu11': 0.0, 'mu02': 878800.0, 'mu30': 0.0, 'mu21': 0.0, 'mu12': 0.0, 'mu03': 0.0, 'nu20': 0.1201923076923077, 'nu11': 0.0, 'nu02': 0.05777777777777778, 'nu30': 0.0, 'nu21': 0.0, 'nu12': 0.0, 'nu03': 0.0}
观察各个轮廓的面积:
轮廓0的面积:14900
轮廓1的面积:34314
轮廓2的面积:3900

在这里插入图片描述

计算轮廓的面积：contourArea函数

opencv 中也有单独计算轮廓面积的函数 contourArea函数

函数 cv2.contourArea()用于计算轮廓的面积。该函数的语法格式为：

retval =cv2.contourArea(contour [, oriented] ))

式中的返回值 retval 是面积值。

式中有两个参数：

contour 是轮廓。
oriented 是布尔型值。当它为 True 时，返回的值包含正/负号，用来表示轮廓是顺时针还是逆时针的。该参数的默认值是 False，表示返回的 retval 是一个绝对值。

代码示例：使用函数 cv2.contourArea()计算各个轮廓的面积。


import cv2
import numpy as np
o = cv2.imread('moments.bmp')
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
 cv2.CHAIN_APPROX_SIMPLE)
cv2.imshow("original",o)
n=len(contours)
contoursImg=[]
for i in range(n):
 print("moments["+str(i)+"]面积=",cv2.contourArea(contours[i]))
 temp=np.zeros(o.shape,np.uint8)
 contoursImg.append(temp)
 contoursImg[i]=cv2.drawContours(contoursImg[i],
 contours,i,(255,255,255),3)
 cv2.imshow("moments[" + str(i)+"]",contoursImg[i])
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：

moments[0]面积= 14900.0
moments[1]面积= 34314.0
moments[2]面积= 3900.0

可以看到跟上面m00 拿到的是一样的，图显也一样
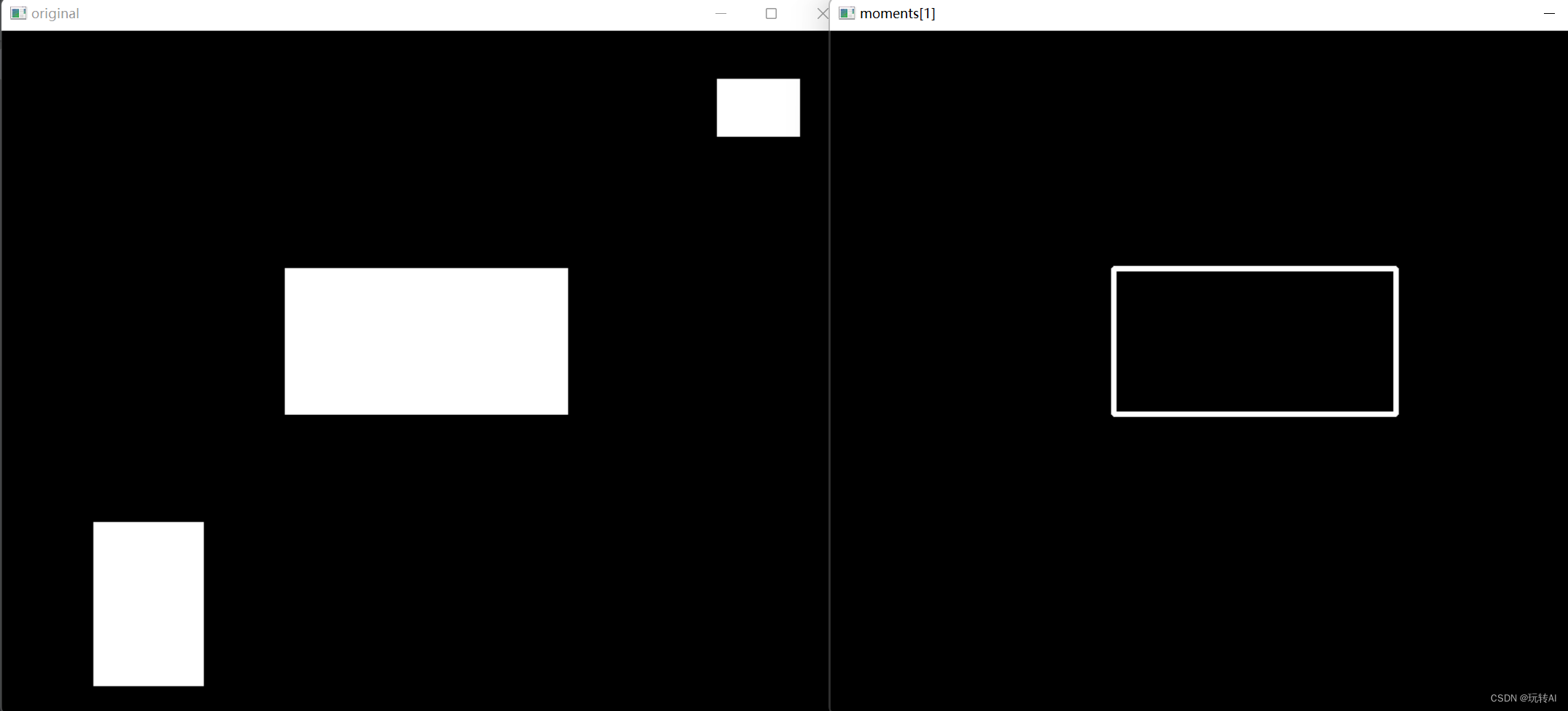
在这里插入图片描述

代码示例：在上面的基础上，将面积大于 15 000 的轮廓筛选出来。

代码如下：

import cv2
import numpy as np
o = cv2.imread('moments.bmp')
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
 cv2.CHAIN_APPROX_SIMPLE)
cv2.imshow("original",o)
n=len(contours)
contoursImg=[]
for i in range(n):

 temp=np.zeros(o.shape,np.uint8)
 contoursImg.append(temp)
 contoursImg[i]=cv2.drawContours(contoursImg[i],
 contours,i,(255,255,255),3)
 if cv2.contourArea(contours[i]) > 15000:
  print("moments[" + str(i) + "]面积=", cv2.contourArea(contours[i]))
  cv2.imshow("moments[" + str(i)+"]",contoursImg[i])
cv2.waitKey()
cv2.destroyAllWindows()

通过语句“if cv2.contourArea(contours[i])>15000:”实现对面积值的筛选，然后对面积值大于 15 000 的轮廓使用语句“cv2.imshow(“contours[” + str(i)+“]”,contoursImg[i])”显示出来。

运行结果：

moments[1]面积= 34314.0

在这里插入图片描述

计算轮廓的长度（周长）：arcLength函数

函数 cv2.arcLength()用于计算轮廓的长度，其语法格式为：

retval = cv2.arcLength( curve, closed )

式中返回值 retval 是轮廓的长度（周长）。

上式中有两个参数：

curve 是轮廓。
closed 是布尔型值，用来表示轮廓是否是封闭的。该值为 True 时，表示轮廓是封闭的

示例：将一幅图像内长度大于平均值的轮廓显示出来。

import cv2
import numpy as np
#--------------读取及显示原始图像--------------------
o = cv2.imread('moments.bmp')

#--------------获取轮廓--------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
#--------------计算各轮廓的长度之和、平均长度--------------------
n=len(contours) # 获取轮廓的个数
cntLen=[] # 存储各轮廓的长度
for i in range(n):
 cntLen.append(cv2.arcLength(contours[i],True))
 print("第"+str(i)+"个轮廓的长度:%d"%cntLen[i])
cntLenSum=np.sum(cntLen) # 各轮廓的长度之和
cntLenAvr=cntLenSum/n # 轮廓长度的平均值
print("轮廓的总长度为：%d"%cntLenSum)
print("轮廓的平均长度为：%d"%cntLenAvr)

运行结果：

第0个轮廓的长度:498
第1个轮廓的长度:782
第2个轮廓的长度:254
轮廓的总长度为：1534
轮廓的平均长度为：511

代码示例原图

在这里插入图片描述