题面

题目描述

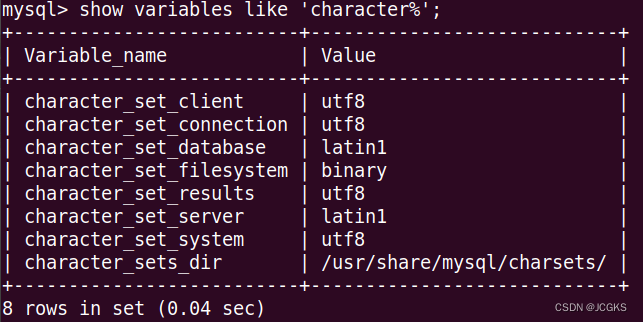
中国象棋半张棋盘如图（a）所示。马自左下角往右上角跳。

今规定只许往右跳，不许往左跳，且要求马跳的方式按照（b）图顺时针深度优先递归。比如图（a）中所示为一种跳行路线。如果马要从 0,0 点，跳到 4,8 点，前 6 种跳法的打印格式如下，请参考前6 种跳的方式，输出马从 0,0 点到 4,8 点所有可能的跳的路线。

1:0,0->2,1->4,2->3,4->4,6->2,7->4,8
2:0,0->2,1->4,2->3,4->1,5->3,6->4,8
3:0,0->2,1->4,2->3,4->1,5->2,7->4,8
4:0,0->2,1->4,2->2,3->4,4->3,6->4,8
5:0,0->2,1->4,2->2,3->4,4->2,5->4,6->2,7->4,8
6:0,0->2,1->4,2->2,3->4,4->2,5->0,6->2,7->4,8

  连接

与卒的遍历十分相似，要注意边界和方向数组的变化和输出格式

#include <bits/stdc++.h>
using namespace std;
int c = 0 , r[450][3];
int fx[5] = {0 , 2 , 1 , -1 , -2},fy[5] = {0 , 1 , 2 , 2 , 1};
void print(int k){
	c++;
	printf("%d:" , c);
	for ( int i = 1 ; i < k ; i++ )
		printf("%d,%d->" , r[i][1] , r[i][2]);
	printf("%d,%d\n" , 4 , 8);
}
void dfs( int x, int y , int k){
	r[k][1] = x;
	r[k][2] = y;
	if(x == 4 && y == 8){
		print(k);
		return;
	}
	int tx , ty;
	for ( int i = 1 ; i <= 4 ; i++ ){
		tx = x + fx[i];
		ty = y + fy[i];
		if ( tx >= 0 && tx <= 4 && ty >= 0 && ty <= 8 )
			dfs(tx , ty , k+1);
	}
}
int main(){
	dfs(0,0,1);
}

骑士巡游

题面

题目描述

马在中国象棋以日字形规则移动，给定n×m 大小的棋盘，以及马的初始位置(x,y) 和目标位置 (s,t)，要求不能重复经过棋盘上的同一个点，计算马至少走多少步可以到达目标位置，所有棋盘保证从初始位置到结束位置一定有路径可达。

输入

测试数据包含一行，为六个整数，分别为棋盘的大小以及初始位置坐标 n,m,x,y,s,t 。（1≤x,s≤n≤5，1≤y,t≤m≤5）

输出

包含一行，为一个整数，表示马能到达目标位置的最小步数。

样例

输入

3 3 1 1 1 3

输出

2

 链接

换皮的迷宫最少步数 ，注意方向数组和回溯的部分

#include <bits/stdc++.h>
using namespace std;
int n , m , s1 , s2 , e1 , e2 , c;
int d[20][20];
bool f[20][20];
int fx[9]={0 , 1,2,2,1,-1,-2,-2,-1},fy[9]={0,2,1,-1,-2,-2,-1,1,2};
void dfs(int x , int y , int k){
	d[x][y] = k;
	if(x == e1 && y == e2){
		return;
	}
	int tx , ty;
	for( int i = 1 ; i <= 8 ; i++ ){
		tx = x + fx[i];
		ty = y + fy[i];
		if( tx >= 1 && tx <= n && ty >= 1 && ty <= m && k + 1 < d[tx][ty] && !f[tx][ty]){
			f[tx][ty] = true;
			dfs(tx , ty , k+1);
			f[tx][ty] = false;
		}
	}
}
int main(){
	scanf("%d%d%d%d%d%d" , &n , &m , &s1 , &s2, &e1 , &e2);
	for (int i = 1; i <= 10; i++) {
    	for (int j = 1; j <= 10; j++) {
        	d[i][j] = INT_MAX;
    	}
	}
	dfs(s1 , s2 , 0);
	printf("%d" , d[e1][e2]);
	return 0;
}