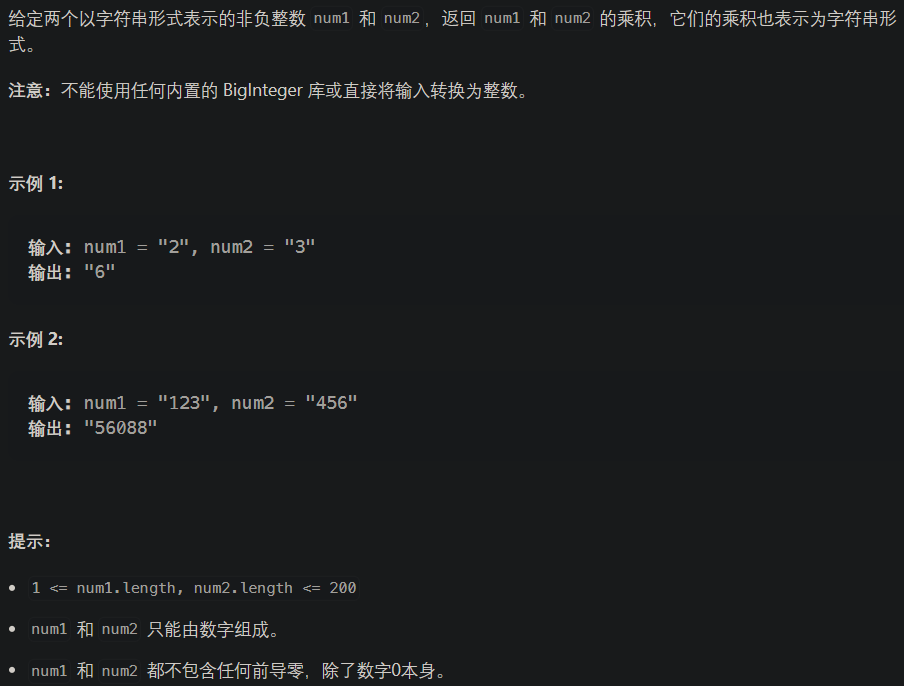
1. 字符串相乘
   

class Solution 
{
public:
	/*
	* 将两个字符串相乘拆分成两步：
	* 先将一个字符串的每个字符与另一个字符串相乘得到一个计算结果
	* 再将所有计算结果的字符串进行相加
	*/
    string multiply(string num1, string num2) 
    {
        string result = "0";
        // 一个字符串为'0'串，结果就为0
        if(num1 == "0" || num2 == "0")
        {
            return result;
        }
		
		// 计算顺序从右向左，就像乘法计算中的从低位向高位的顺序
        for(size_t i = num1.size(); i > 0; --i)
        {
        	// 字符与字符串相乘
            string tmp = subMultiply(num1[i - 1], num2, num1.size() - i);
            // 字符串相加
            result = addStrings(result, tmp);
        }
        return result;
    }
    // 字符与字符串相乘的计算. n表示的是计算结果串需要补几个0
    string subMultiply(char c, string num, size_t n)
    {
        int carry = 0;
        int mul = 0;
        for(size_t i = num.size(); i > 0; --i)
        {
            mul = (c - '0') * (num[i - 1] - '0') + carry;
            carry = mul / 10;
            num[i - 1] = ((mul % 10) + '0');
        }
        if(carry != 0)
        {
            num.insert(0, 1, carry + '0');
        }
        while(n--)
        {
            num += '0';
        }
        return num;
    }
	// 两个字符串相加的计算
    string addStrings(string num1, string num2)
    {
        size_t index1 = num1.size() - 1;
        size_t index2 = num2.size() - 1;
        
        string result;
        int sum = 0;
        int carry = 0;
        while(index1 != -1 && index2 != -1)
        {
            sum = num1[index1--] - '0' + num2[index2--] - '0' + carry;
            result += ((sum % 10) + '0');
            carry = sum / 10;
        }

        while(index1 != -1)
        {
            sum = num1[index1--] - '0' + carry;
            result += ((sum % 10) + '0');
            carry = sum / 10;
        }

        while(index2 != -1)
        {
            sum = num2[index2--] - '0' + carry;
            result += ((sum % 10) + '0');
            carry = sum / 10;
        }

        if(carry != 0)
        {
            result += (carry + '0');
        }

        reverse(result.begin(), result.end());
        return result;
    }
};

2. 电话号码的字母组合
   

const static vector<string> num2str = { "","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz" };
class Solution
{
public:
    void recursion(string::iterator itBegin, string::iterator itEnd, vector<string>& ret, string& str)
    {
        string newStr = str; // 用一个新的字符串保存str的原始数据，防止丢失
        if (itBegin != itEnd)
        {
            size_t n = *itBegin - '0';
            for (size_t i = 0; i < num2str[n].size(); ++i)
            {
                str = newStr; // 保证每次循环都是原始数据
                str += num2str[n][i];
                recursion(itBegin + 1, itEnd, ret, str);
            }
        }
        else
        {
            ret.push_back(str);
        }
    }
    vector<string> letterCombinations(string digits)
    {
        vector<string> ret;
        // digits.size() == 0 直接跳出结束
        if (digits.begin() != digits.end())
        {
      		// 获取第1个digit
            string::iterator pc = digits.begin();
            // 计算下标，和字符串对应
            size_t n = (*pc) - '0';
            // 遍历字符串，同时递归
            for (size_t i = 0; i < num2str[n].size(); ++i)
            {
                string str; // 每次循环，str都会清空
                str += num2str[n][i];
                recursion(digits.begin() + 1, digits.end(), ret, str);
            }
        }

        return ret;
    }
};

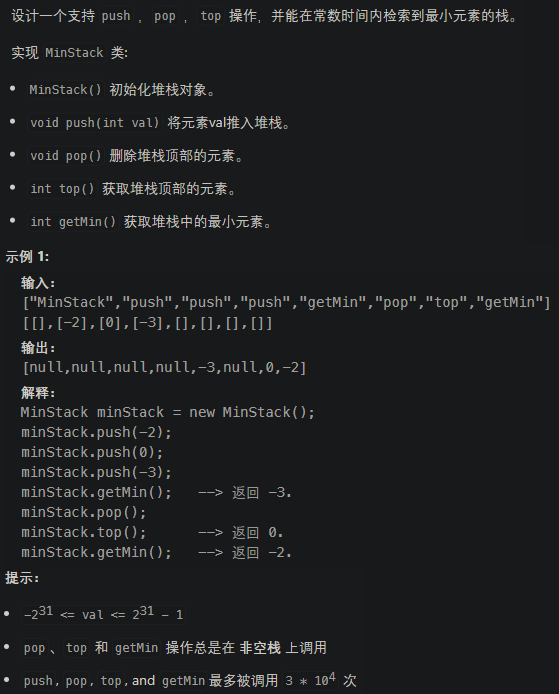
3. 最小栈
   

class MinCount
{
public:
	// 存最小值及其计数
    MinCount(int min, int count = 1)
        : _min(min)
        , _count(count)
    {}
public:
    int _min;
    int _count;
};

class MinStack
{
public:
    void push(int val)
    {
        _st.push(val);
        // 新的最小值被push
        if (_minst.empty() || val < _minst.top()._min)
        {
            _minst.push(MinCount(val));
        }
        // 最小值不变，计数+1
        else if (val == _minst.top()._min)
        {
            ++(_minst.top()._count);
        }
    }

    void pop()
    {
    	// 被pop的值如果是最小值进入判断
        if (_st.top() == _minst.top()._min)
        {
            if (_minst.top()._count > 1)
            {
                --(_minst.top()._count);
            }
            else
            {
                _minst.pop();
            }
        }
        
        _st.pop();
    }

    int top()
    {
        return _st.top();
    }

    int getMin()
    {
        return _minst.top()._min;
    }
private:
    stack<int> _st;
    stack<MinCount> _minst;
};

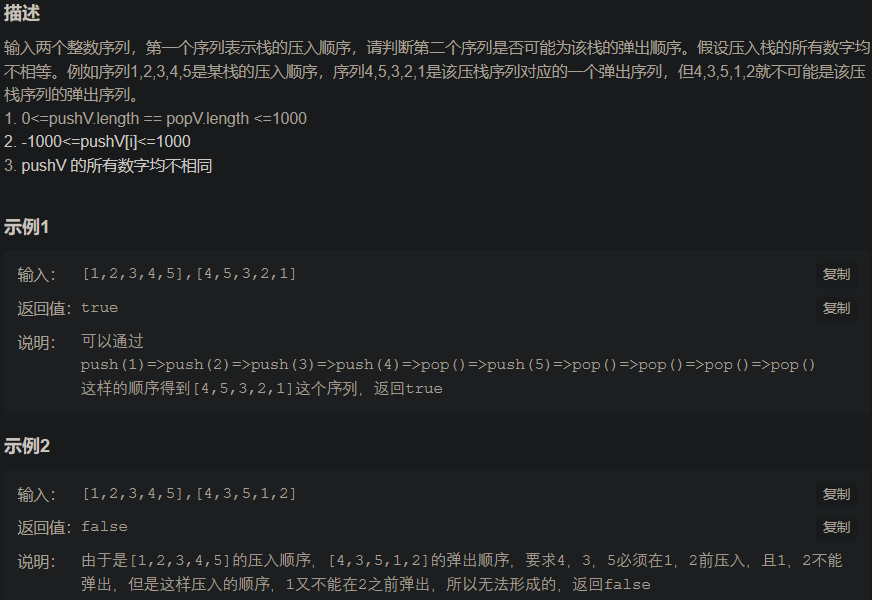
4. 栈的压入、弹出序列
   

#include <stack>
class Solution 
{
public:
    bool IsPopOrder(vector<int>& pushV, vector<int>& popV) 
    {
        size_t pushI = 0;
        size_t popI = 0;
        stack<int> st;
        while(pushI < pushV.size())
        {
            if(pushV[pushI] != popV[popI])
            {
                st.push(pushV[pushI]);
            }
            else 
            {
                ++popI;
                while(!st.empty() && st.top() == popV[popI])
                {
                    st.pop();
                    ++popI;
                }
            }
            ++pushI;
        }
        
        return st.empty();
    }
};

5. 逆波兰表达式求值
   

class Solution 
{
public:
    int evalRPN(vector<string>& tokens) 
    {
        int num1 = 0;
        int num2 = 0;
        stack<int> st;

        for(string& s : tokens)
        {
            if(s == "+")
            {
                num2 = st.top();
                st.pop();
                num1 = st.top();
                st.pop();
                st.push(num1 + num2);
            }
            else if(s == "-")
            {
                num2 = st.top();
                st.pop();
                num1 = st.top();
                st.pop();
                st.push(num1 - num2);
            }
            else if(s == "*")
            {
                num2 = st.top();
                st.pop();
                num1 = st.top();
                st.pop();
                st.push(num1 * num2);
            }
            else if(s == "/")
            {
                num2 = st.top();
                st.pop();
                num1 = st.top();
                st.pop();
                st.push(num1 / num2);
            }
            else
            {
                st.push(stoi(s));
            }
        }
        return st.top();
    }
};

6. 数组中的第K个最大元素
   

class Solution 
{
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
    	// 向下建堆时间复杂度O(logN)
        priority_queue<int> pq(nums.begin(), nums.end());
        while(--k)
        {
            pq.pop();
        }
        return pq.top();
    }
};