CV-对比学习-模型：MoCo/SimCLR/BYOL/SimSiam

news2024/10/5 16:25:28

很多大佬认为，深度学习的本质就是做两件事情：Representation Learning（表示学习）和 Inductive Bias Learning（归纳偏好学习）。在表示学习方面，如果直接对语义进行监督学习，虽然表现很好，但是它需要很多的样本并且往往是需要对特定的任务进行设计，很难具有迁移性。所以难怪各位大佬们都纷纷为自监督学习站台，自监督是未来！

自监督学习有大类方法，一个是生成方法一个对比方法，如上图。生成方法往往会对像素级损失进行约束，关于这一类笔者已经在之前的文章中进行了整理，而对比学习在表示学习上做的事情就是： 其实模型不必要知道关于特征的细节，只要学到的特征足以使其和其他样本区别开来就行。

Contrastive loss


对比损失 Contrastive loss，简单的解释就是，利用对比正-负样本来学习表示。学习的目的为：

这里 x+ 是与 x 相似或相等的数据点，称为正样本。x− 是与 x 不同的数据点，称为负样本。score 函数是一个度量两个特征之间相似性的指标，直接算内积来表示：

然后尝试优化以下期望，即让正例样本越相似，要负例样本越远就好。

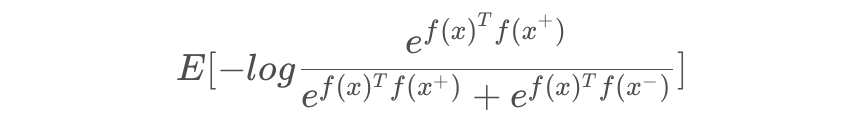
其实这个叫法最初似乎出自 Yann LeCun “Dimensionality Reduction by Learning an Invariant Mapping”，本来是用于处理在降维空间中正样本和负样本之间的相似/不相似的远近距离关系，式子为：

其中  ，代表两个样本特征的欧氏距离，y 为两个样本是否匹配的标签，y=1 代表两个样本相似或者匹配，y=0 则代表不匹配，margin 为设定的阈值。

损失函数主要惩罚如果原本相似的样本 y=1，但在特征空间的欧式距离较大，则说明当前的模型不好，损失变大。同样的如果原本不相似 y=0，但其特征空间的欧式距离反而小的话，损失也会变大。

上图是 loss 与样本特征的欧式距离 d 之间的关系，其中红色虚线表示的是相似样本的损失值，蓝色实线表示的不相似样本的损失值。

def contrastive_loss(self, y,d,batch_size):
      tmp= y *tf.square(d)
      #tmp= tf.mul(y,tf.square(d))
      tmp2 = (1-y) *tf.square(tf.maximum((1 - d),0))
      return tf.reduce_sum(tmp +tmp2)/batch_size/2   

而这种成对 loss 的思想在其他领域如搜索推荐会有其他的变体：

  • Pairwise Ranking Loss

  • Triplet Ranking Loss

而马上要总结的 MoCo 使用的其实是 Contrastive loss 一种变体 InfoNCE：

一个正例 ，K 个负例  ，这样可以使只有真正匹配（与 query q 算点积）的样本更相似，并且同时不匹配的不相似时，loss 才低。最初出自 Contrastive Predictive Coding，据说使用 InfoNCE，可以同时优化 encoder 和自回归模型。

如何选择正-负例pair？


Easy negative example 比较容易识别，所以相对来说找一些较难的 pair 是有利于训练的。一般可分为：

  • Offline mining：计算所有的数据的 embedding，然后计算所以 pair 之间的距离判断其难易程度，主要选择 hard 或者 semi-hard 的数据。

  • Online mining：为每一 batch 动态挖掘有用的数据，将一个 batch 输入到神经网络中，得到这个 batch 数据的 embedding，Batch all 的方式还是会计算所有的合理的，Batch hard 偏向于选择距离最大的正样本和距离最小的负样本。

这里需要思考的问题是这种 pair 对究竟多少数量是合适的？

一般来说，对比方法在有更多的负样本的情况下效果更好，因为假定更多的负样本可以更有效地覆盖底层分布，从而给出更好的训练信号。

所以回到 MoCo 的图了，既然样本数量对于学习到的样本质量有很大的影响，那么我们就扩展负样本的数量就好！但是目前对于 batch size 是没有很好的解决办法的，实际上如下图 a，loss 的梯度会流过编码器的正样本 q 和负样本 k 的 Encoder。

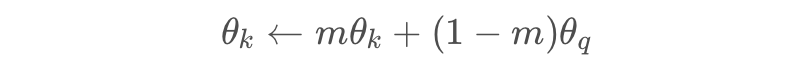
这意味着样本的数量被限制在 mini-batch 的尺寸上，即我们并不能采样无穷多的样本，GPU 负载能力有限。

对于查询正样本  ，要在一个 batch 中（dictionary size = mini-batch size）的所有 K 中区别开来，有上图三种方法：

  • end-to-end：先编码 encoder（可同可不同），然后内积算 loss 再梯度。但是这种方法由于 dictionary size 和 mini-batch 的强耦合性（负例样本对也会为 loss 产生贡献，也会回传梯度），在 batch 大的时候优化难，而在 batch 小的时候，batch 之间的参数会不一样，也就是 GPU 大小限制了模型的性能。

  • memory bank：把 dictionary size 从 mini-batch 中解耦出来，即先把所有样本的特征保存下来 bank，然后每次随机采样，再梯度 query 的 encoder 的参数。但是这样只有当所有 key 被 sample 完以后才会更新 memory bank，不同的 key 在和 query 是不一致的和滞后的，因为每一次 sample encoder 都会更新虽有 memory bank 后面也加入了 momentum，但是是针对 sample 来的，在更新 memory bank 时会保留一部分上一轮的特征值。

  • MoCo：是以上两者的融合版本，将 dictionary 作为一个 queue 进行维护当前的negative candidates pool，且它是改成了 queue 的动态更新机制，每 sample 一个 batch key（所以一个 trick 就是会使用 Shuffling BN，打乱再 BN），进队后相对于一些最早进入队列的 mini-batch 对应的 key 进行出队操作，这样保证一些过时的、一致性较弱的 key 可以被清除掉。这样就同样是解耦，K 是队列长度，K 可以设置很大，同时更新也不会有问题。

按照以上伪码，可以简单看看 MoCo 的三个比较重要的函数：

@torch.no_grad()
    def _momentum_update_key_encoder(self):
        """
        key encoder的Momentum update
        """
        for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
            param_k.data = param_k.data * self.m + param_q.data * (1. - self.m)

    @torch.no_grad()
    def _dequeue_and_enqueue(self, keys):
        """
        完成对队列的出队和入队更新
        """
        # 在更新队列前得到keys
        keys = concat_all_gather(keys)#合并所有keys

        batch_size = keys.shape[0]

        ptr = int(self.queue_ptr)
        assert self.K % batch_size == 0  # for simplicity

        # 出队入队完成队列的更新
        self.queue[:, ptr:ptr + batch_size] = keys.T
        ptr = (ptr + batch_size) % self.K  # 用来移动的指针

        self.queue_ptr[0] = ptr

    def forward(self, im_q, im_k):
        # 计算query features
        q = self.encoder_q(im_q)  # queries: NxC
        q = nn.functional.normalize(q, dim=1)

        # 计算key features
        with torch.no_grad():  # 对于keys是没有梯度的反向的
            self._momentum_update_key_encoder()  # 用自己的来更新key encoder

            # 执行shuffle BN
            im_k, idx_unshuffle = self._batch_shuffle_ddp(im_k)

            k = self.encoder_k(im_k)  # keys: NxC
            k = nn.functional.normalize(k, dim=1)

            # 还原shuffle
            k = self._batch_unshuffle_ddp(k, idx_unshuffle)

        # 计算概率
        # positive logits: Nx1
        l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1) #用爱因斯坦求和来算sum
        # negative logits: NxK
        l_neg = torch.einsum('nc,ck->nk', [q, self.queue.clone().detach()])

        # logits: Nx(1+K)
        logits = torch.cat([l_pos, l_neg], dim=1)

        # 平滑softmax的分布，T越大越平
        logits /= self.T

        # labels是正例index
        labels = torch.zeros(logits.shape[0], dtype=torch.long).cuda()

        # 出队入队更新
        self._dequeue_and_enqueue(k)

        return logits, labels

论文链接：

https://arxiv.org/abs/1911.05722


代码链接：

https://github.com/facebookresearch/moco

完整的中文源码阅读笔记：

https://github.com/nakaizura/Source-Code-Notebook/tree/master/MoCo

SimCLR


MoCo 强调 pair 对的样本数量对对比学习很重要，SimCLR 认为构建负例的方式也很重要。先说结论：

  • 多个数据增强方法组合对于对比预测任务产生有效表示非常重要。此外，与有监督学习相比，数据增强对于无监督学习更加有用；

  • 在表示和对比损失之间引入一个可学习的非线性变换可以大幅提高模型学到的表示的质量；

  • 与监督学习相比，对比学习得益于更大的批量和更多的训练步骤。

模型过程如下：

  • 先 sample 一些图片（batch）

  • 对 batch 里的 image 做不同的 data augmentation，如图上的  和 ，将其视为正对；

  • 一个基本的神经网络编码器 f(·)，从增强数据中提取表示向量， 作者使用 ResNet-50；

  • 一个小的神经网络投射头（projection head）g(·)，将表示映射到对比损失的空间；

  • 目标是希望同一张图片、不同 augmentation 的结果相近，并互斥其他结果。

作者认为多种数据增强操作的组合是学习良好表示的关键，论文里面主要讨论过的有如下：


推荐有一个 github 用于数据增强很好用，pip install imgaug：

https://github.com/aleju/imgaug

为什么要用非线性的projection head？

由图可知在 representation 与 contrastive loss 间使用了可学习的 non-linear projection，这个其实是非常简单的单层 MLP+ReLU 的架构。其优势在于避免计算 similarity 的 loss function 在训练时丢掉一些重要的 feature，可以改善之前的层的表示质量。

损失函数 NT-Xent（the normalized temperature-scaled cross entropy loss），  和  是从 Projection Head 获得的输出矢量，output∈{0,1} if k≠i，τ 表示温度参数可以用来放缩概率。

值得注意的一个 trick 就是会算两次（即公式中间的 2N，会把 i-j 的计算，用 j-i 成对的再算一次）

做完训练后，特征表示可以拿去下游做微调，比如用于图像分类等下游任务。整体的框架图如下：

论文链接：

https://arxiv.org/abs/2002.05709


代码链接：

https://github.com/google-research/simclr

注：他们用了 128 块 GPU/TPU，来处理每个 minibatch 9000 个以上样本（这是为了获得足够的负样本对比，所以必须要比普通的 batch 要大），并完成 1000 轮的训练。

MoCo v2

在 MoCo 的基础上加入了 SimCLR 的 projection head 和多种数据增强手段如模糊等。ImageNet 任务提升了 6%。

SimCLR v2
 

结合无监督预训练、半监督训练、有监督的微调和未标记数据的蒸馏等等一系列的训练手段。具体如下图：

  • 左边，非监督的方法学习一个任务无关的通用的表征，这里直接用 SimCLR，不同点在于网络变大和也借用了 MoCo 部分架构。

  • 中间，用监督的方法进行 fine-turning

  • 右边，在 unlabeled 大数据集上进行蒸馏

这种架构显然很适合在工业界落地。

BYOL

无需负样本也能够取得好的效果？！出自 DeepMind的 NIPS20’的Bootstrap Your Own Latent（BYOL），BYOL 认为之前的方法都基于 negative pairs，而它们很大程度上取决于图像增强的选择，所以为什么不直接从图像增强视角出发呢？框架图如下：

没有 pair，但是 BYOL 使用两个相互交互并相互学习的神经网络，分别称为在线网络和目标网络。架构如上：

  • 上面的分支是 online network，包括了 embedding，projection 以及 prediction，其中嵌入的使我们最要想要的模块。

  • 下面的分支是 target network，包括 embedding 和 projection 。

  • online 网络参数使用 L2 的梯度进行更新，而 target 网络直接通过 online 的 momentum 得到，这里 target 的就充当了之前负样本的功能。

即 target 可以随机开始得到输出比如一开始的结果为 1.4% 非常差，此时新开一个分支训练 online 去预测同一图像在不同增强视角下的 target 的表示（从一个分支直接预测了另一个分支的输出，用滚动编码方法更新），此时结果居然就可以到非常高的程度了。

也正是 BYOL 主打其 不需要进行 negative 样本的 idea。所以因此它的性能对 batch size 的大小不是特别敏感，在同等参数量的情况下，BYOL 的效果也是非常好。

为什么BYOL有效？

最近有一篇论文对其做了细致的测试，其中最关键的结论就是：BYOL 移除 BN 之后的表现就和随机瞎猜一样了。由于 BN 的出现本来就是为了克服 domain 和 target 的差异问题，即预防 mode collapse，可以将正负样本的距离拉开，所以 BYOL 可能也是做了这样的事情，做了对图片均值和方差的学习，然后重新分配结果和特征值。

BYOL和MoCo、SimCLR的区别

  • MoCo、SimCLR 更偏向于问这两张图片之间有何差异？

  • BYOL 可能是在问这张图片与这些图片的平均有什么差异？

论文链接：

https://arxiv.org/abs/2006.07733

SimSiam

孪生网络已成为无监督表达学习领域的通用架构，现有方法通过最大化同一图像的两者增广之后的相似性使其避免“崩溃解（collapsing solutions）”问题。即在训练网络的时候，网络会很迅速找了一个退化解并达到了最小可能损失 -1。

但是在 kaiming 大神的这篇文章中，他们提出的 Simple Siamese（SimSiam）网络不仅可以没有 negative sample pairs；没有 arge batch；甚至没有 momentum encoders 就学到有意义的特征表达。

主要是提出 stop-grad 的概念，结构如下：

前面的部分基本相同，输入两个随机变换的  和 ，通过相同的孪生网络提取特征并变换到高维空间，然后可以看到左边的分支有个 projection head h 得到 ，之后再与右边得到的  ，两者的结果进行匹配使 cosine 最小化：

而重点的 Stop-gradient，意思是在 loss 的第一项的时候，  不会从  接收梯度信息；同时在计算第二项，则会从  接收梯度信息，即 loss 变为：

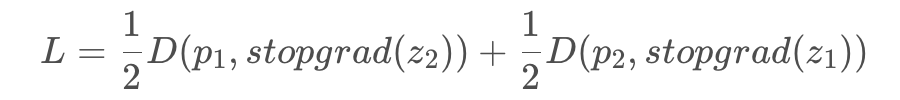
# Algorithm1 SimSiam Pseudocode, Pytorch-like
# f: backbone + projection mlp。f是backbone+projection head部分组成
# h: prediction mlp
for x in loader: # load a minibatch x with n samples
  x1, x2 = aug(x), aug(x) # random augmentation，随机增强后的x1和x2
  #分别做两次投影操作
  z1, z2 = f(x1), f(x2) # projections, n-by-d
  p1, p2 = h(z1), h(z2) # predictions, n-by-d
  #计算不对称的两个D得到loss L
  L = D(p1, z2)/2 + D(p2, z1)/2 # loss
  L.backward() # back-propagate，反向传播
  update(f, h) # SGD update，梯度更新

def D(p, z): # negative cosine similarity
  z = z.detach() # stop gradient，在这里使用detach做stopgrad的操作
  p = normalize(p, dim=1) # l2-normalize
  z = normalize(z, dim=1) # l2-normalize
return -(p*z).sum(dim=1).mean()

其实 stopgrad 的本质就是一个交替方案（固定一个，求解另一个）的近似求解。

论文链接：

https://arxiv.org/abs/2011.10566

最后再看个对比方便分清楚：

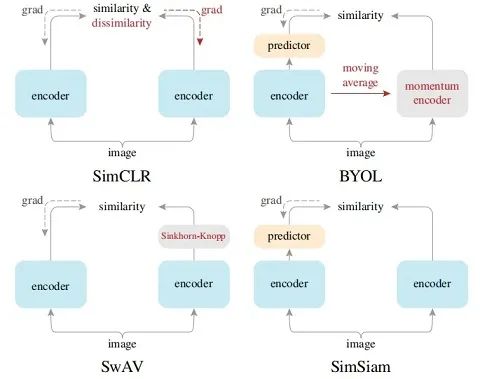
盘点近期大热对比学习模型：MoCo/SimCLR/BYOL/SimSiam - 专知

一文梳理无监督对比学习（MoCo/SimCLR/SwAV/BYOL/SimSiam）_code_kd的博客-CSDN博客_simclr code

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/84565.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

海泰隐私计算能力助力实现数据“可用不可见”

海泰隐私计算能力助力实现数据“可用不可见”

一、 数据孤岛阻碍数据发展 当今时代，信息技术日新月异，人类文明正经历从信息科技（IT)时代向数据科技(DT）时代的飞速变革。数据作为基础性战略资源的地位日益凸显。然而，数据孤岛问题突出。出于对数据安全的传统保护&…
阅读更多...
单商户商城系统功能拆解45—应用中心—积分商城

单商户商城系统功能拆解45—应用中心—积分商城

单商户商城系统，也称为B2C自营电商模式单店商城系统。可以快速帮助个人、机构和企业搭建自己的私域交易线上商城。 单商户商城系统完美契合私域流量变现闭环交易使用。通常拥有丰富的营销玩法，例如拼团，秒杀，砍价，包邮…
阅读更多...
pikachu靶场-2 跨站脚本漏洞（xss）

pikachu靶场-2 跨站脚本漏洞（xss）

跨站脚本漏洞（xss） Cross-Site Scripting 简称为“CSS”，为避免与前端叠成样式表的缩写"CSS"冲突，故又称XSS。一般XSS可以分为如下几种常见类型： 1.反射性XSS; 2.存储型XSS; 3.DOM型XSS; XSS漏洞一直被评估…
阅读更多...
Kubernetes二进制多节点集群部署

Kubernetes二进制多节点集群部署

多Maser集群架构的了解 Kubernetes作为容器集群系统，通过健康检查重启策略实现了Pod故障自我修复能力，通过调度算法实现将Pod分布式部署，并保持预期副本数，根据Node失效状态自动在其他Node拉起Pod，实现了应用层的高可用…
阅读更多...
羧基聚乙二醇叠氮 COOH-PEG-N3/Azide的结构式

羧基聚乙二醇叠氮 COOH-PEG-N3/Azide的结构式

叠氮化物与炔烃之间的反应能够使羧酸PEG有效缀合到目标分子或材料上，并且产率很高。 所得羧酸可与胺，羟基和其他基团反应。 叠氮化物和羧酸之间的PEG接头具有良好的水溶性，较小的位阻和增强的稳定性。 产品名称 羧基聚乙二醇叠氮 COOH-PEG…
阅读更多...
css div等块元素设置display:inline-block存在间隙问题

css div等块元素设置display:inline-block存在间隙问题

我们给块元素例如div设置display:inline-block&#xff0c;会发现元素之间存在空隙。如下图。 <div class"contain"><div id"box1"></div><div id"box2"></div><div id"box3"></div> <…
阅读更多...
Simulink自动化-Matlab脚本自动生成Autosar RTE S/R接口及mapping

Simulink自动化-Matlab脚本自动生成Autosar RTE S/R接口及mapping

文章目录前言设计Excel模板Input/Output属性Sender/Receiver属性Matlab脚本自动创建Input/Output接口自动创建RTE Sender/Receiver port实现效果Excel设置运行新建Input与Output运行创建RTE Port及Mapping总结前言 在之前的一篇文章中&#xff0c;介绍了Autosar Parameter Por…
阅读更多...
内网隧道各类协议方法

内网隧道各类协议方法

正+反（了解即可） 正向代理：已控服务器监听端口，通过这个端口形成一个正向的隧道，由代理机器代替主机去访问内网目标。但是内网入口一般处于DMZ区域有防火墙拦截，无法直接进入内网环境。 反向代理：由内网主机主动交出权限到代理机器，然后本地去连接形成反向代理。例如…
阅读更多...
吉林优美姿文化：抖音账号怎么做垂直？

吉林优美姿文化：抖音账号怎么做垂直？

其实现在抖音限流看起来是一件很平常的事情&#xff0c;那么在我们抖音运营中&#xff0c;如果出现一些不合规的行为或者怎么样的&#xff0c;都会导致限流&#xff0c;严重的可能还会被限流&#xff0c;那么这时候怎么办呢&#xff1f;跟着吉林优美姿小编来一起看看吧&#xf…
阅读更多...
MySql索引简单知识点及事务的分析

MySql索引简单知识点及事务的分析

目录 索引 什么是MySql索引&#xff1f; 索引的易忽略点 基本操作&#xff1a; 查看索引 创建索引 删除索引 索引在MySql中的数据结构 事务 使用方法 事务的核心特性 隔离性 隔离的常见问题 ***MySql四个隔离级别 &#x1f4cc;————本章重点————&#x1f…
阅读更多...
微软艰难的2022安全年回顾

微软艰难的2022安全年回顾

©网络研究院 这些是管理员需要了解的 2022 年以来最重要的漏洞和修复。 我们即将结束 2022 年的安全年。只有时间会告诉我们 2023 年会发生什么&#xff0c;但对于 Microsoft 网络的 IT 和安全管理员来说&#xff0c;2022 年是混合攻击、本地 Exchange Server 缺陷和需要…
阅读更多...
【Python】向量叉积和凸包 | 引射线法 | 葛立恒扫描法

【Python】向量叉积和凸包 | 引射线法 | 葛立恒扫描法

猛戳&#xff01;跟哥们一起玩蛇啊 &#x1f449; 《一起玩蛇》&#x1f40d; &#x1f4ad; 写在前面&#xff1a;这个系列似乎反响不错&#xff0c; 所以我继续水下去 &#xff08;bushi&#xff09;。本篇博客是关于经典的 Cross Product and Convex Hull &#xff08;向量叉…
阅读更多...
最大正方形问题

最大正方形问题

最大正方形问题 作者&#xff1a;Grey 原文地址&#xff1a; 博客园&#xff1a;最大正方形问题 CSDN&#xff1a;最大正方形问题 题目描述 在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内&#xff0c;找到只包含 ‘1’ 的最大正方形&#xff0c;并返回其面积。 题目链接见&am…
阅读更多...
数字式压力闭环放大器|比例溢流阀闭环控制器

数字式压力闭环放大器|比例溢流阀闭环控制器

控制不同带压力反馈信号输入&#xff08;0~10V或4~20mA&#xff09;比例压力阀、比例溢流阀、比例节流阀、比例插装阀&#xff0c;带位置反馈信号输入比例流量阀等。斜坡上升和下降时间独立调整(0.05~10 s)。10V参考电压输出外部电位器控制。最大驱动电流 0.4~3A&#xff0c;最…
阅读更多...
4个月高效学习，我是如何从手工测试做到测试开发的？

4个月高效学习，我是如何从手工测试做到测试开发的？

向上的路很难走&#xff0c;但一旦踏上去&#xff0c;每一步都算数&#xff01; 为什么必须转型为测试开发&#xff1f; 不懂开发的手工测试是新时代“文盲” 在移动互联网和大数据时代&#xff0c;为满足市场和业务需求&#xff0c;互联网应用既要实现产品功能快速迭代&…
阅读更多...
java字符串中常用的10个方法

java字符串中常用的10个方法

文章目录前言一、字符串的构造1.使用常量进行直接赋值构造2.使用new String对象3.使用字符数组进行构造二、字符串的比较1.比较2.equals方法比较3. compareTo方法比较4.compareToIgnoreCase(String str)方法三、字符串的查找1.charAt(int index)方法2.indexOf(String str)方法四…
阅读更多...
网络流量分析帮助企业提升OA应用性能（二）

网络流量分析帮助企业提升OA应用性能（二）

需求简介 某外高桥公司的OA系统是其重要的业务系统&#xff0c;OA系统负责人表示&#xff0c;部分用户反馈&#xff0c;访问OA系统时比较慢。需要通过分析系统看一下实际情况。 信息部已对企业领导定义了独立的组&#xff0c;本次要主动分析领导们的使用体验快慢。如果OA系统…
阅读更多...
mmdetection3d S3DIS （持续更新）

mmdetection3d S3DIS （持续更新）

Mmdetection3d集成了大量3D深度学习算法&#xff0c;其中很大一部分可以在室内三维数据集S3DIS上运行。本节重点介绍S3DIS数据集及其在mmdetection3d中的预处理程序。 1 S3DIS S3DIS&#xff08;Stanford Large-Scale 3D Indoor Spaces Dataset &#xff09;数据集是斯坦福大学…
阅读更多...
【R语言】白葡萄酒的EDA分析

【R语言】白葡萄酒的EDA分析

白葡萄酒的EDA分析1.项目相关信息1.1 评估标准1.2 项目模板1.3 数据集列表1.4 项目示例1.5 数据选择1.5.1 选择1.5.2 详细数据说明1.5.3 有关项目提交的常见问题2.环境准备2.1 导入相关包2.2 加载数据集2 数据整理2.1 数据评估2.1.1 质量类问题2.1.2 结构性问题2.1 数据清洗2.1…
阅读更多...
二叉树的代码实现和详解

二叉树的代码实现和详解

树的定义 树是由n&#xff08;n>1&#xff09;个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树&#xff0c;也就是说它是根朝上&#xff0c;而叶朝下的。 树具有以下特点&#xff1a; 1.每个结点有零个或多个子结点&#xff1b; 2.没有父…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023