【Python】向量叉积和凸包 | 引射线法

猛戳！跟哥们一起玩蛇啊 👉 《一起玩蛇》🐍

💭 写在前面：这个系列似乎反响不错， ~~所以我继续水下去~~ （bushi）。本篇博客是关于经典的 Cross Product and Convex Hull （向量叉积和凸包）的，我们将介绍引射线法，葛立恒扫描法。在讲解之前我会对前置知识做一个简单的介绍，比如向量叉积，如何确定直线是在顺时针上还是逆时针上等。算法讲解部分是为后面练习题做准备的，比如如何判断内点是否在多边形内，如何计算多边形面积等，还将简单介绍一下葛立恒扫描法，在提供的练习题中就能碰到。练习代码量200行左右，如果感兴趣想尝试做的话，需要有一定的耐心。练习题的环境为 Google Colaboratory（K80 GPU）Jupyter Notebook：colab

【高级软件实习】向量叉积和凸包 | 引射线法 | 判断点是否在多边形内部 | 葛立恒扫描法 | Cross Product and Convex Hul

Ⅰ. 前置知识

0x00 向量叉积（Cross product）

📚 概念：向量积 (Cross product)，也可以称之为 "向量叉积" 。我更愿意称之为 "向量叉积"，因为可以顾名思义 —— 叉积，交叉乘积！

" 叉积，叉积……积……？！积你太美！"

咳咳…… 它是一种在向量空间中向量的二元运算。

向量叉积不同于点积！其运算结果是一个向量，而非标量。

并且两个向量的叉积与这两个向量垂直。表示方法为 $v_1 \times v_2$ ，期中 $v$ 代表向量。

💭 定义如下：

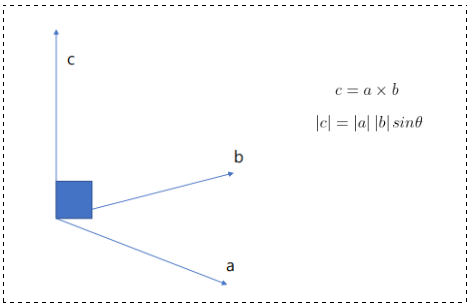
模长：这里的 $\theta$ 表示两向量之间的夹角（共起点的前提下），范围 $0^{\circ} \leq \theta \leq 180^{\circ}$ ，它位于这两个矢量所定义的平面上。

方向：a向量与b向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。

$c$ 的长度在数值上等于以 $a,b$ ，夹角为 $\theta$ 组成的平行四边形面积。
因为在不同的坐标系中 $c$ 可能不同，所以运算结果 $c$ 是一个伪向量。

两向量的三角形的面积：

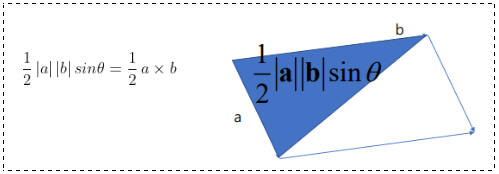
令向量 $a$ 和 $b$ 都在平面 $xy$ 上：

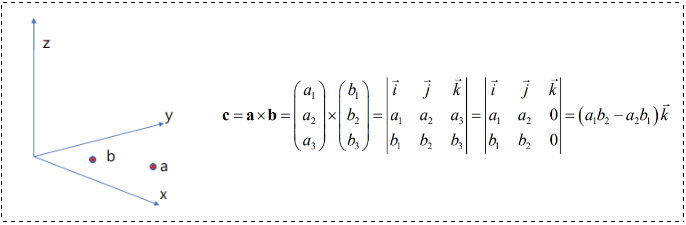
0x01 确定顺时针逆时针（Clockwise or Counter-clockwise）

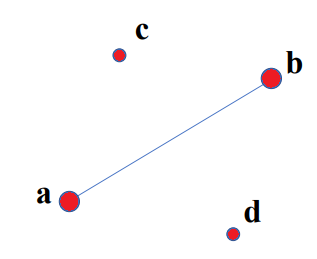
❓ 有什么好办法，可以确定点在直线 $a,b$ 是在顺时针上还是逆时针上？

我们可以用叉积 "暗中观察" 点是否在直线 $a\, b$ 的顺时针或逆时针方向上：

∵ $(b-a)\times (c-a)$ 的叉积指向显示的前方，∴ $C$ 点在逆时针方向。
∵ $(b-a)\times (d-a)$ 的叉积指向显示的后方，∴ $D$ 点在顺时针方向。

0x02 交叉点（Intersection）

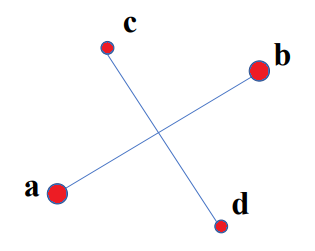
当每条线的端点位于另一条线的不同侧面时，两条线就会交叉：

Ⅱ. 算法讲解部分

0x00 判断内点是否在多边形内（Inner points）

❓ 思考：如何检查平面上的一个点（point）是否在多边形内部？

这里我介绍两种常用的方法，只在一侧法 和 引射线法。

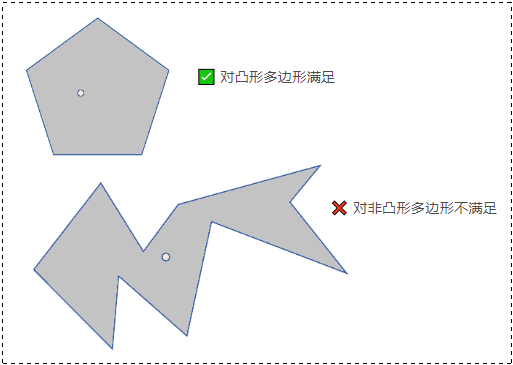
① "只在一侧" 法：

只在一侧 (only on the one side) ，当一个点在每个多边形边的一侧（顺时针或逆时针）时，该点就在多边形的内部。

② 引射线法：

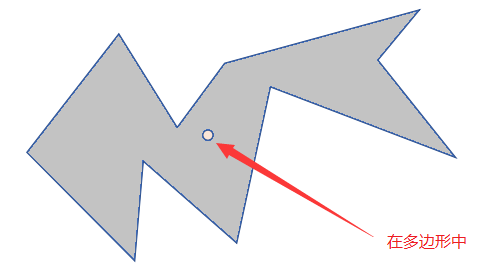
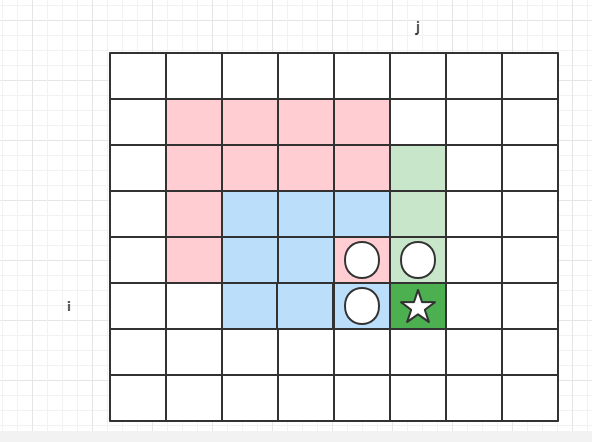
从目标点出发引一条射线，观察这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。

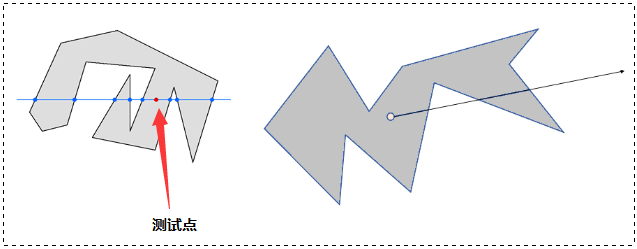
图中的红点是需要测试的点（我已标出），我们要确定它是否位于多边形内。

💡 解决方案：将多边形的每一边与测试点的 $Y$ （垂直）坐标进行比较，并编译一个结点列表，其中每个节点是一个边与测试点的 $Y$ 阈值相交的点。在此示例中的多边形的 8 条边越过 $Y$ 阈值，而其他 6 条边则没有。那么，如果有奇数测试点每边的节点数，那就说明它在多边形内。如果测试点的每一侧都有偶数个节点，那么它在多边形之外。

在本示例中，测试点左侧有5个节点，右侧有3个节点。由于 5 和 3 是奇数，该测试点在多边形内。（注意：该算法不关心多边形是顺时针还是逆时针跟踪）

0x01 计算多边形的面积

💡 思路：

按逆时针方向对顶点进行排序。
找到 $(i+1)$ 个顶点位于第 $i$ 个节点和第 $i+1$ 个节点的边缘的顺时针方向的三角形，并积累三角形的面积。
删除三角形并再次重复该过程，直到没有顶点为止。

将所有边缘的叉积加起来，然后除以2。

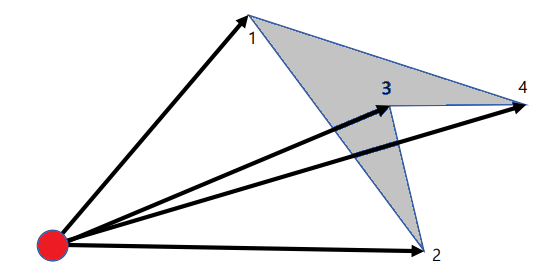
sum += float(x1 * y2 - x2 * y1);

根据一条边的方向，添加或减去三角形的面积。

令人惊讶的是，只留下了多边形的面积：

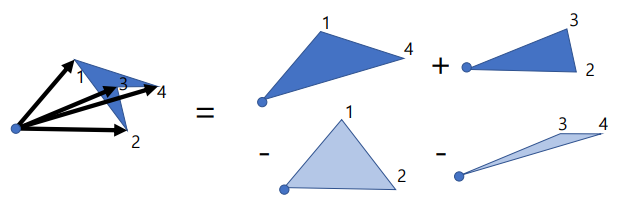
🔑 提示：其类似于边的叉积之和

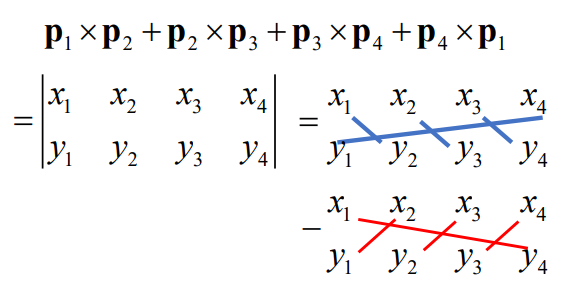
0x02 葛立恒扫描法（Graham Scan）

凸包计算（Computing a convex hull），给定平面点：

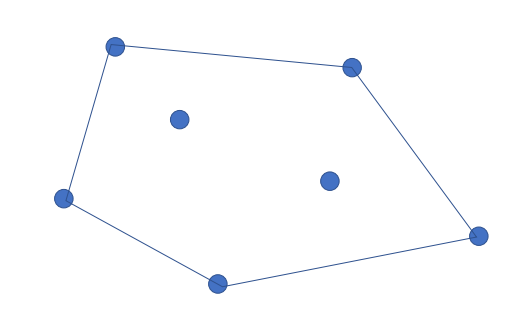
葛立恒扫描法（Graham Scan）

葛立恒扫描法（Graham's scan）是一种计算一组的平面点的凸包的算法。以在1972年发表该算法的葛立恒命名。

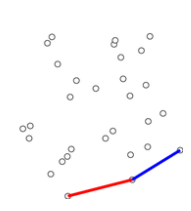
先找到左下角的点 $P_0$ （一定在凸包上）。
以 $P_0$ 为原点，将其他的点按照极坐标排序，角度小的排在前，若角度相同，距离近的排在前。
$P_0,P_1$ 入栈，从 $P_2$ （第三个点）开始，若 $P_2$ 在直线 $P_0 P_1(\, p\, [ i-1 ] \, p [ i ]\, )$ 的左边，则 $P_2$ 入栈，否则 $P_1$ 出栈，一直遍历完后面所有点（这里就需要向量叉乘来判断点在线的左边还是右边）。
最后留在栈中的点就是凸包上的点。

Ⅲ. 练习（Assignment）

🔺 注意：需用 Python 实现，算法必须在不导入外部库的情况下实现，但允许使用 numpy、math、sort 相关函数。（如果不加以限制，直接导某包掉函数就能直接算凸包，那还练个锤子，知道的小伙伴可以在评论区扣出来）

环境推荐：Colab

任务1：计算多边形面积

给定由 $N$ 个点构成的平面多边形，计算该多边形的面积。

input

Output

0 0

2 0

2 2

1 1

0 2

任务2：多边形坐标

给定的 $N$ 个构成多边形的点和 $M$ 个检查点，判断每个检查点是否在多边形内。

* 注：在边缘线上的点也视作在多边形内。

input

Output

5 // N points

0 0 // (x1, y1)

2 0 // (x2, y2)

2 2

1 1

0 2

0 0

0.5 0.5

-1 -1

Inside

Outside

读取 input1.txt , input2, input3.txt，将结果分别生成到 output1.txt , _output3.txt 。

这里的 txt 文件请复制粘贴下面的数据，请自行创建！

💬 input1.txt

💬 input2.txt

💬 input3.txt

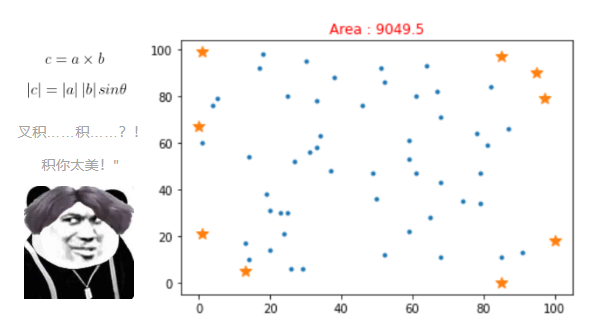
输出文件命名为 output1, output2, output3，输出结果演示：

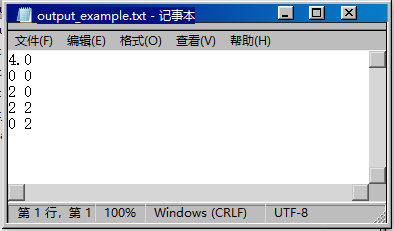
生成 output 文件后，每个 output 都要画出图像，这里就不需要大家自己画了，

提供了 display.py，这是用于生成图像的代码。

def display(input_txt_path, output_txt_path):
    import matplotlib.pyplot as plt
    
    '''
    input1:input_txt_path=input_example.txt的路径
    input2:output_txt_path=output_example.txt的路径
    return：保存conex_hull图像
    '''
    
    with open(input_txt_path, "r") as f:
        input_lines = f.readlines()
    with open(output_txt_path, "r") as f:
        output_lines = f.readlines()
        
    whole_points = input_lines
    area = round(float(output_lines[0]), 1)
    hull_points = output_lines[1:]

    x_list = [int(x.split(" ")[0]) for x in whole_points]
    y_list = [int(x.split(" ")[1]) for x in whole_points]
    plt.plot(x_list, y_list, marker='.', linestyle='None')

    hx_list = [int(x.split(" ")[0]) for x in hull_points]
    hy_list = [int(x.split(" ")[1]) for x in hull_points]

    plt.plot(hx_list, hy_list, marker='*', linestyle='None', markersize=10)

    title = plt.title(f'Area : {area}')
    plt.setp(title, color='r')
    plt.savefig(output_txt_path[:-3]+"png", bbox_inches='tight')


if __name__ == "__main__":
    input_txt_path = "./input_example.txt"
    output_txt_path = "./output_example.txt"
    display(input_txt_path, output_txt_path)

通过调用提供的 display 函数，生成的图像效果如下：

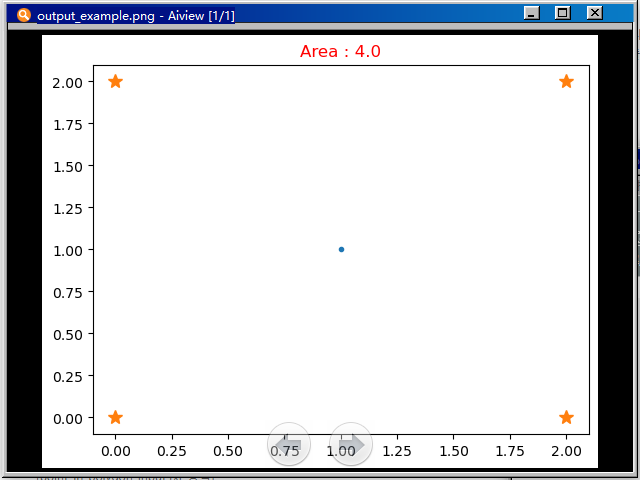
任务3：点是否在多边形内

给定 $N$ 个点构成平面多边形，计算凸包及其面积。

input

Output

5 // N 个点

0 0 // (x1, y1)

2 0 // (x2, y2)

2 2

1 1

0 2

(0, 0), (2, 0), (2, 2), and (0, 2) are points of convex hull.

您可以从 point_in_polygon_input.txt 输入 5 个坐标，并将它们与在刚才实现的 "练习1" 中保存的output1, output2, output3.txt 的多边形进行比较，以 "in" 或 "out" 的形式输入5个坐标。

这里的 point_in_polygon_input.txt 仍然是要自己创建，复制粘贴手动创建：

point_in_ploygon_input.txt：

因此，与3个 output1-3.txt 的文件相比，必须生成 3 个output 文件，格式演示如下：

参考代码

# -*- coding: utf-8 -*-
import math

def read_points(p):
    L = []  
    with open(p, 'r') as FILE:
        line = FILE.readlines()

    Lx, Ly = [int(i.split(" ")[0]) for i in line], [int(i.split(" ")[1]) for i in line]
    
    cur, sz = 0, len(Lx)
    for cur in range(sz):
        x, y = Lx[cur], Ly[cur]
        L.append(
            (x, y)
        )

    return L

def get_rad(px, py):
    pi = math.pi

    a = px[0] - py[0]
    b = px[1] - py[1]

    if a == 0:
        if b:
            return pi / 2
        else:
            return -1

    rad = math.atan(float(b) / float(a))

    if rad < 0:
        return rad + pi
    else:
        return rad


def sort_points_tan(p, pk):
    L = []
    resL = []

    i = 0
    sz = len(p)
    for i in range(sz):
        L.append({"index": i, "rad": get_rad(p[i], pk)})
    L.sort(key=lambda k: (k.get('rad')))

    sz = len(L)
    for i in range(sz):
        resL.append(p[L[i]["index"]])

    return resL


def calc_area(points):
    sz = len(points)
    points.append(points[0])
    S = 0
    for i in range(sz):
        S += (points[i][0] + points[i + 1][0]) * (points[i + 1][1] - points[i][1])
    return abs(S) / 2


def convex_hull(p):
    p = list(set(p))
    
    k = 0
    sz = len(p)
    for i in range(1, sz):
        if p[i][1] < p[k][1]:
            k = i
        if (p[i][0] < p[k][0]) and (p[i][1] == p[k][1]):
            k = i

    pk = p[k]
    p.remove(p[k])
    p_sort = sort_points_tan(p, pk)
    L = [pk, p_sort[0]]

    sz = len(p_sort)
    for i in range(1, sz):
        while (( (L[-2][0] - L[-1][0]) * (p_sort[i][1] - L[-1][1]) - (p_sort[i][0] - L[-1][0]) * (L[-2][1] - L[-1][1]) ) > 0):
            L.pop()
        L.append(p_sort[i])

    return L


def check(sp, ep, p):
    if sp[0] < p[0] and ep[1] > p[1]: 
        return False
    if sp[1] == p[1] and ep[1] > p[1]: 
        return False
    if ep[1] == p[1] and sp[1] > p[1]: 
        return False
    if sp[1] == ep[1]: 
        return False
    if sp[1] > p[1] and ep[1] > p[1]: 
        return False
    if sp[1] < p[1] and ep[1] < p[1]: 
        return False
    if ep[0] - (ep[0] - sp[0]) * (ep[1] - p[1]) / (ep[1] - sp[1]) < p[0]: 
        return False
    return True


def inpoly(p, poly_points):
    cnt = 0
    i = 0
    sz = len(poly_points)
    for i in range(sz):
        p1, p2 = poly_points[i], poly_points[(i + 1) % sz]
        if check(p1, p2, p):
            cnt += 1

    if cnt % 2 == 1:
        return True
    else:
        return False



def write_in_out(test_points, poly_points, out_txt_path):
    with open(out_txt_path, "w") as FILE:
        i = 0
        for i in test_points:
            if inpoly(i, poly_points):
                FILE.write("in")
            else:
                FILE.write("out")
            FILE.write("\n")
def write_area(poly_points,out_path):
    res = convex_hull(poly_points)

    with open(out_path,"w") as FILE:
        FILE.write(str(calc_area(res)))
        FILE.write('\n')
        sz = len(res)

        for i in range(sz - 1) :
            FILE.write(str( res[i][0]))
            FILE.write(" ")
            FILE.write(str(res[i][1]))
            FILE.write("\n")
    return res


test_points = read_points("point_in_polygon_input.txt")
poly_out_path = "foxny_point_in_polygon_output1.txt" #####
poly_points = read_points("input1.txt")  ####
area = write_area(poly_points, "foxny_output1.txt")  ######
write_in_out(test_points , area, poly_out_path)

def display(input_txt_path, output_txt_path):
    import matplotlib.pyplot as plt
    
    '''
    input1 : input_txt_path = path of input_example.txt
    input2 : output_txt_path = path of output_example.txt
    return : save convex_hull image
    '''
    
    with open(input_txt_path, "r") as f:
        input_lines = f.readlines()
    with open(output_txt_path, "r") as f:
        output_lines = f.readlines()
        
    whole_points = input_lines
    area = round(float(output_lines[0]), 1)
    hull_points = output_lines[1:]

    x_list = [int(x.split(" ")[0]) for x in whole_points]
    y_list = [int(x.split(" ")[1]) for x in whole_points]
    plt.plot(x_list, y_list, marker='.', linestyle='None')

    hx_list = [int(x.split(" ")[0]) for x in hull_points]
    hy_list = [int(x.split(" ")[1]) for x in hull_points]

    plt.plot(hx_list, hy_list, marker='*', linestyle='None', markersize=10)

    title = plt.title(f'Area : {area}')
    plt.setp(title, color='r')
    plt.savefig(output_txt_path[:-3]+"png", bbox_inches='tight')

####################################################################################1
if __name__ == "__main__":
    input_txt_path = "input1.txt"
    output_txt_path = "foxny_output1.txt"
    display(input_txt_path, output_txt_path)

""

🚩 结果演示：

foxny_output1.png

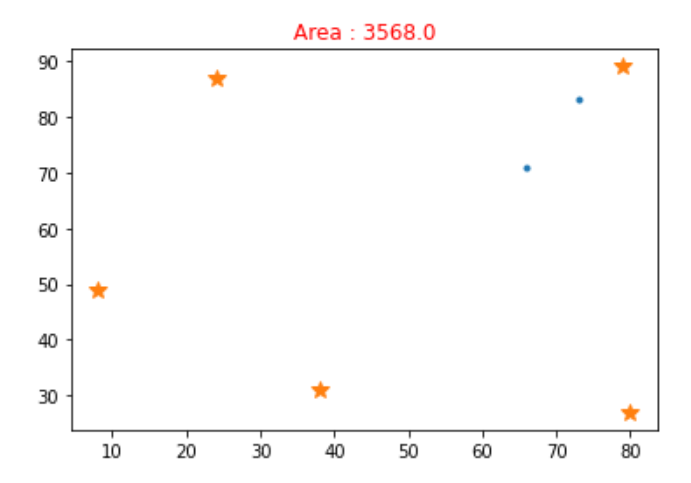
foxny_ouput2.txt

foxny_output2.png

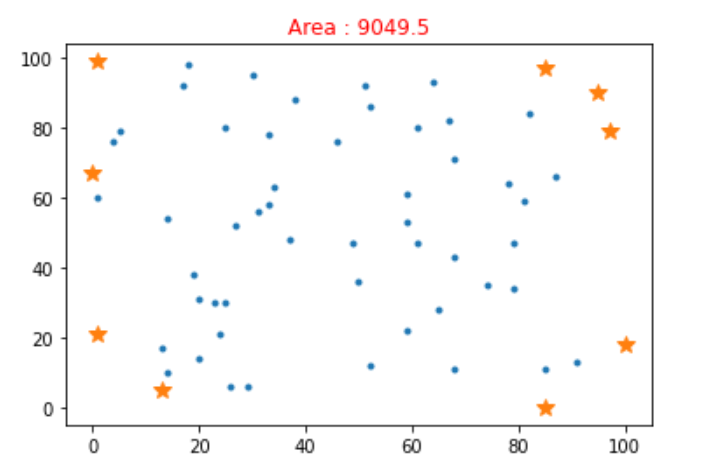
foxny_output2.txt

foxny_output3.png

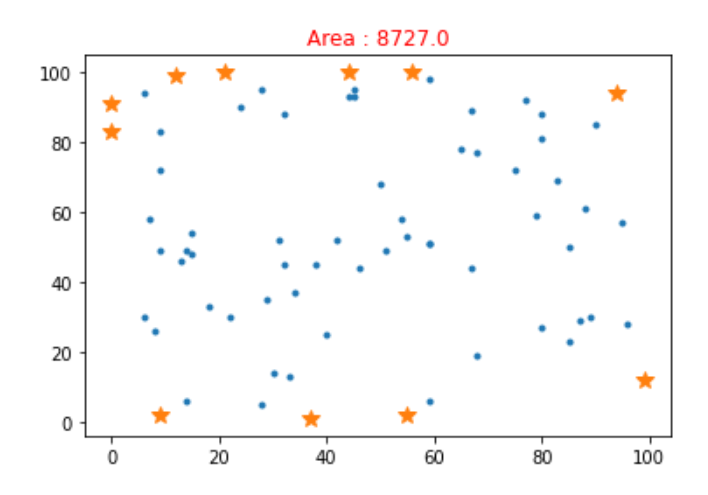
foxny_output3.txt

foxny_point_in_polygon_output1.txt

out
out
out
in
in

foxny_point_in_polygon_output2.txt

out
out
in
in
in

foxny_point_in_polygon_output3.txt

out
out
in
in
in

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2022.12.12
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料

Darel Rex Finley. Point-In-Polygon Algorithm — Determining Whether A Point Is Inside A Complex Polygon[EB/OL]. 1998,2006,2007[2022.12.12]. http://alienryderflex.com/polygon/.

C++reference[EB/OL]. []. http://www.cplusplus.com/reference/.

Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .

百度百科[EB/OL]. []. https://baike.baidu.com/.