树的定义

树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
树具有以下特点：
1.每个结点有零个或多个子结点；
2.没有父结点的结点为根结点；
3.每一个非根结点只有一个父结点；
4.每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树；

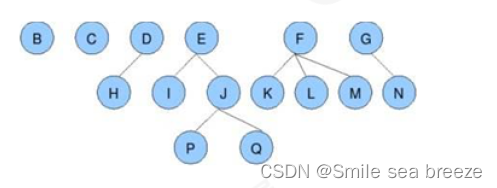
树的相关概念

结点的度：
一个结点含有的子树的个数称为该结点的度；
叶结点：
度为0的结点称为叶结点，也可以叫做终端结点
分支结点：
度不为0的结点称为分支结点，也可以叫做非终端结点
结点的层次：
从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推
结点的层序编号：
将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数。
树的度：
树中所有结点的度的最大值
树的高度(深度)：
树中结点的最大层次
森林：
m（m>=0）个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林；给森林增加一个统一的根
结点，森林就变成一棵树

孩子结点：
一个结点的直接后继结点称为该结点的孩子结点
双亲结点(父结点)：
一个结点的直接前驱称为该结点的双亲结点
兄弟结点：
同一双亲结点的孩子结点间互称兄弟结点

二叉树基本定义

二叉树就是度不超过2的树(每个结点最多有两个子结点)
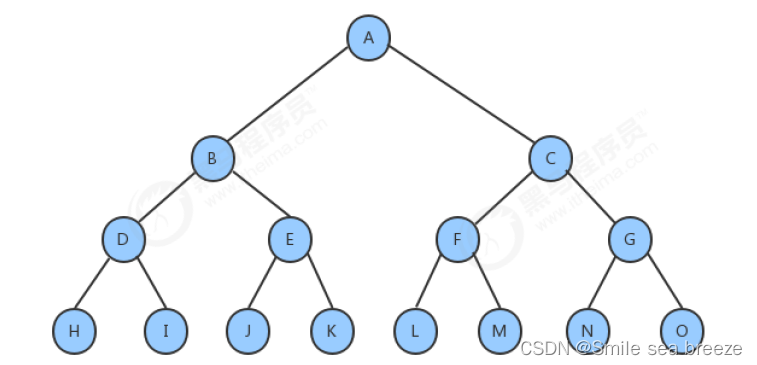
满二叉树：
一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树

完全二叉树：
叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
在这里插入图片描述

二叉树的创建

在这里插入图片描述

private class Node<Key,Value>{
	//存储键
	public Key key;
	//存储值
	private Value value;
	//记录左子结点
	public Node left;
	//记录右子结点
	public Node right;
	public Node(Key key, Value value, Node left, Node right) {
		this.key = key;
		this.value = value;
		this.left = left;
		this.right = right;
	}
}

二叉树的代码的API设计

在这里插入图片描述

代码实现方法

实现思想

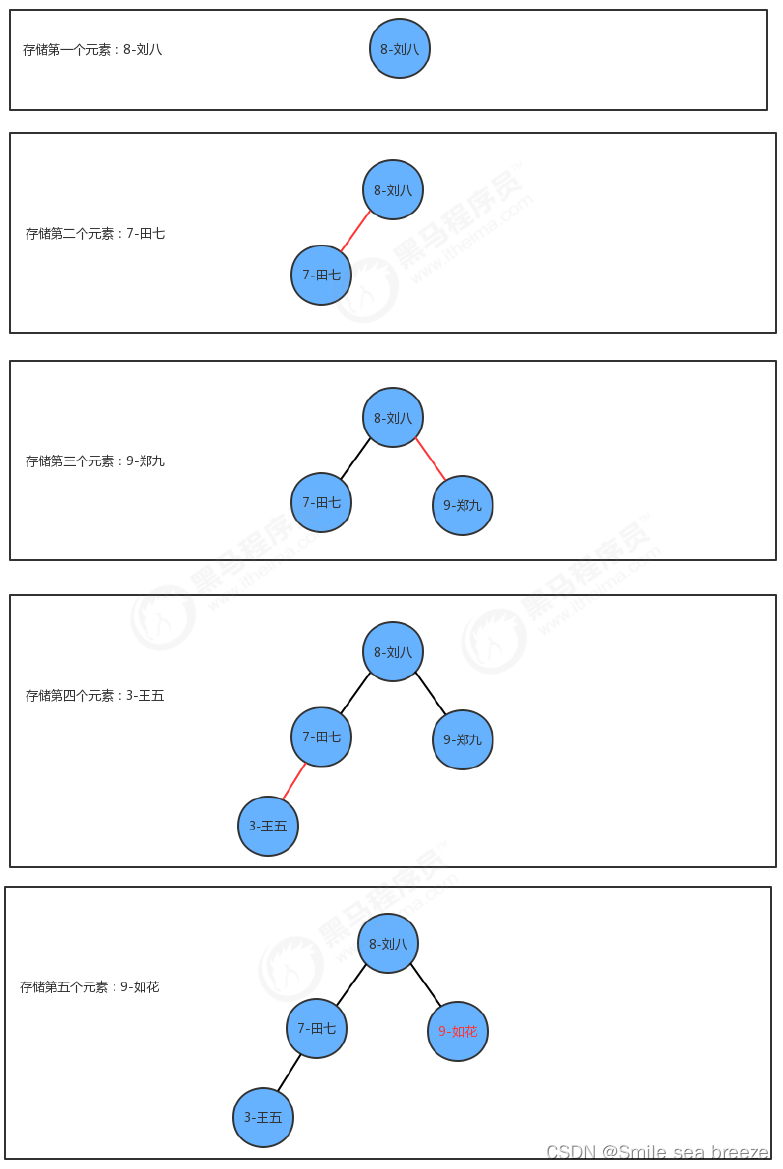
插入方法put实现思想：
1.如果当前树中没有任何一个结点，则直接把新结点当做根结点使用
2.如果当前树不为空，则从根结点开始：
2.1如果新结点的key小于当前结点的key，则继续找当前结点的左子结点；
2.2如果新结点的key大于当前结点的key，则继续找当前结点的右子结点；
2.3如果新结点的key等于当前结点的key，则树中已经存在这样的结点，替换该结点的value值即可。

查询方法get实现思想：
从根节点开始：
1.如果要查询的key小于当前结点的key，则继续找当前结点的左子结点；
2.如果要查询的key大于当前结点的key，则继续找当前结点的右子结点；
3.如果要查询的key等于当前结点的key，则树中返回当前结点的value。
删除方法delete实现思想：
1.找到被删除结点；
2.找到被删除结点右子树中的最小结点minNode
3.删除右子树中的最小结点
4.让被删除结点的左子树称为最小结点minNode的左子树，让被删除结点的右子树称为最小结点minNode的右子
树
5.让被删除结点的父节点指向最小结点minNode

代码实现:

public class BinaryTree<Key extends Comparable<Key>,Value> {
    public static void main(String[] args) throws Exception {
        BinaryTree<Integer, String> bt = new BinaryTree<>();
        bt.put(4, "二哈");
        bt.put(1, "张三");
        bt.put(3, "李四");
        bt.put(5, "王五");
        System.out.println(bt.size());
        bt.put(1, "老三");
        System.out.println(bt.get(1));
        System.out.println(bt.size());
        bt.delete(1);
        System.out.println(bt.size());
    }
    private class Node{
        public Key key;
        private Value value;
        public Node left;
        public Node right;


        public Node(Key key, Value value, Node left, Node right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }
    private Node root;//根结点
    private int N; //记录树中的元素个数
    public int size(){
        return N;
    }//获取树中的元素个数
    public void put(Key key, Value value){
        root =put(root,key,value);
    }//向树中添加元素key-value

    private Node put(Node x, Key key, Value value) {//向指定树中添加key-value,并返回田间元素后新的树
        if(x==null){
            N++;
            return new Node(key,value,null,null);


        }
        int cmp = key.compareTo(x.key);
        if(cmp>0){
            x.right=put(x.right,key,value);//新结点的key大于当前结点的key，继续找当前结点的右子结点
        }else if(cmp<0){
            x.left=put(x.left,key,value); //新结点的key小于当前结点的key，继续找当前结点的右左子结点
        }else{
            x.value=value;//新结点的key等于当前结点的key，把当前结点的value进行替换
        }
        return x;
    }

    public Value get(Key key){//查询树中指定key对应的value
        return get(root,key);
    }

    public Value get (Node x,Key key){ ///从指定的树x中，查找key对应的值
        if(x==null){
            return null;
        }
        int cmp =key.compareTo(x.key);
        if(cmp>0){
           return get(x.right,key);//如果要查询的key大于当前结点的key，则继续找当前结点的右子结点；
        }else if(cmp<0){
           return get(x.left,key);//如果要查询的key小于当前结点的key，则继续找当前结点的左子结点；
        }else{
            return x.value;//如果要查询的key等于当前结点的key，则树中返回当前结点的value。
        }


    }
    //删除树中key对应的value
    public void delete(Key key) {//删除树中key对应的value
        root = delete(root, key);
    }
    public Node delete(Node x,Key key){//删除指定树x中的key对应的value，并返回删除后的新树
        if(x==null){
            return null;
        }
        int cmp=key.compareTo(x.key);
        if(cmp>0){
            x.right=delete(x.right,key);//新结点的key大于当前结点的key，继续找当前结点的右子结点
        }else if(cmp<0){//新结点的key小于当前结点的key，继续找当前结点的左子结点
            x.left = delete(x.left,key);
        }else{
            //新结点的key等于当前结点的key,当前x就是要删除的结点
            //1.如果当前结点的右子树不存在，则直接返回当前结点的左子结点
            if(x.right==null){
                return x.left;
            }
            if(x.left ==null){
                return x.right;
            }
            //3.当前结点的左右子树都存在
            //3.1找到右子树中最小的结点
            Node minNode = x.right;
            while (minNode.left != null) {
                minNode = minNode.left;
            }
            //3.2删除右子树中最小的结点
            Node n = x.right;
            while (n.left != null) {
                if (n.left.left == null) {
                    n.left = null;
                } else {
                    n = n.left;
                }
            }
            //3.3让被删除结点的左子树称为最小结点minNode的左子树，让被删除结点的右子树称为最小结点minNode的右子树
            minNode.left = x.left;
            minNode.right = x.right;
            //3.4让被删除结点的父节点指向最小结点minNode
            x = minNode;
            //个数-1
            N--;
        }
        return x;
        }
    }