💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者
📝目前更新:🌟🌟🌟电力系统相关知识,期刊论文,算法,机器学习和人工智能学习。
🚀支持:🎁🎁🎁如果觉得博主的文章还不错或者您用得到的话,可以关注一下博主,如果三连收藏支持就更好啦!这就是给予我最大的支持!
👨🎓博主课外兴趣:中西方哲学,送予读者:
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“真理”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎

📋📋📋本文目录如下:⛳️⛳️⛳️
目录
1 概述
2 数学模型
3 多目标遗传算法和多目标粒子群算法
4 运行结果
5 Matlab代码+数据+文档讲解
1 概述
分布式系统具有高利用率、高可扩展性和并行性的优点,可以并行运行以处理计算密集型问题。此外,从分布式结构中衍生出几个难题,例如节点之间的通信问题、系统资源和计算节点的映射和分配问题。
高层体系结构(HLA)广泛用于分布式仿真开发。虽然HLA支持大规模分布式仿真,但仿真过程中的负载平衡机制尚未标准化。当仿真系统在非优化分配条件下运行时,由于计算量不足,会出现负载不平衡问题。
负载平衡的结果表现在以下两个方面:一是有效缩短任务的平均响应时间,即尽量缩短仿真过程的运行时间,使系统能够稳定、平稳地运行;其次,最大限度地利用整个系统的仿真资源,减少不必要的资源浪费。
高层体系结构(HLA)是分布式仿真系统的软件体系结构规范,不涉及负载平衡。因此,在HLA的仿真过程中,无法解决仿真时间长和仿真任务分布不均匀引起的失真问题。本文将研究基于组件级的仿真系统,并解决负载不平衡问题。目标是找到一组帕累托最优解,以最小化模型中具有负载限制约束的计算负载和总通信负载的不平衡。为了解决这个问题,提出了一个新的整数规划模型。采用带精英策略的非支配排序遗传算法(NSGA-II)和多目标粒子群优化算法(MOPSO)求解该问题。分析了MOPSO的不同全局最优选择方法(拥挤距离、自适应网格和综合排序)和扰动方法(快速下降和精英学习策略)。由于算法的参数对其性能有显著影响,因此使用具有新响应值的田口方法来调整所提出算法的参数。五个性能指标用于评估这些算法的结果。基于这些结果,将使用网络控制仿真平台来测试和验证这些方案。数值结果表明,提出的带ELS算子的多粒子群优化算法在求解该问题上优于其他提出的算法。此外,所提出的策略可以解决基于HLA的系统中的负载不平衡问题。
2 数学模型
本文考虑了一个具有计算和通信负载限制的双目标负载平衡问题。如前所述,该问题受到分布式仿真系统中负载分配问题的启发,即HLA。在基于HLA的分布式仿真系统中,仿真任务可以分为联邦成员级和组件级。
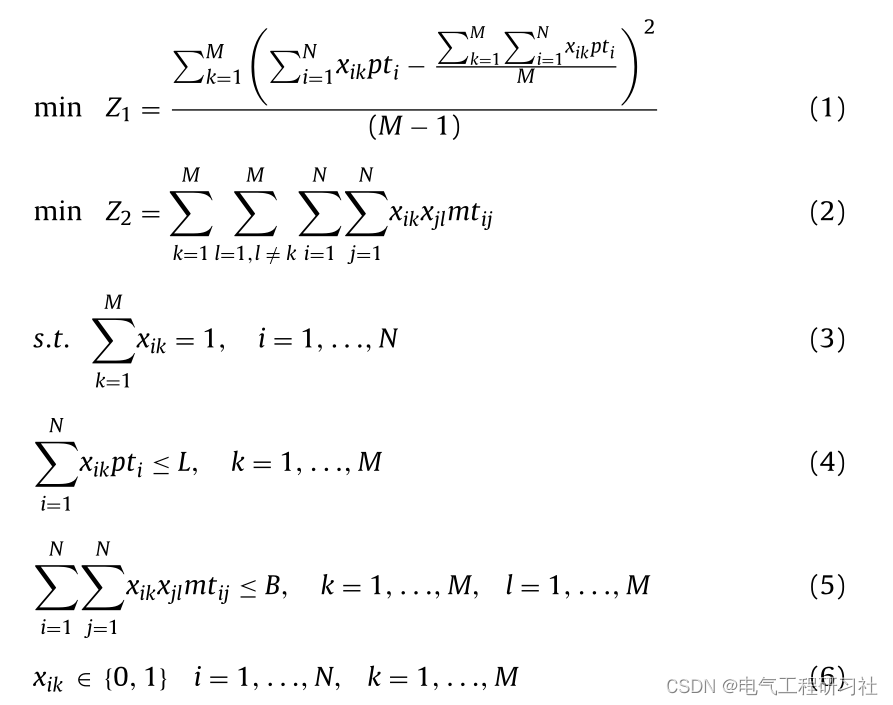
等式(1)最小化了模拟节点计算负载的方差。等式(2)最小化了仿真节点之间的总通信负载。等式(3)规定每个模拟任务被精确地分配给一个模拟节点。等式(4)确保了计算负载限制。等式(5)保证了通信负载限制。等式(6)表示变量的非负性和完整性。更多细节参考第五部分,文件夹里面有详细讲解。
3 多目标遗传算法和多目标粒子群算法
见第五部分,详细文章讲解。
4 运行结果
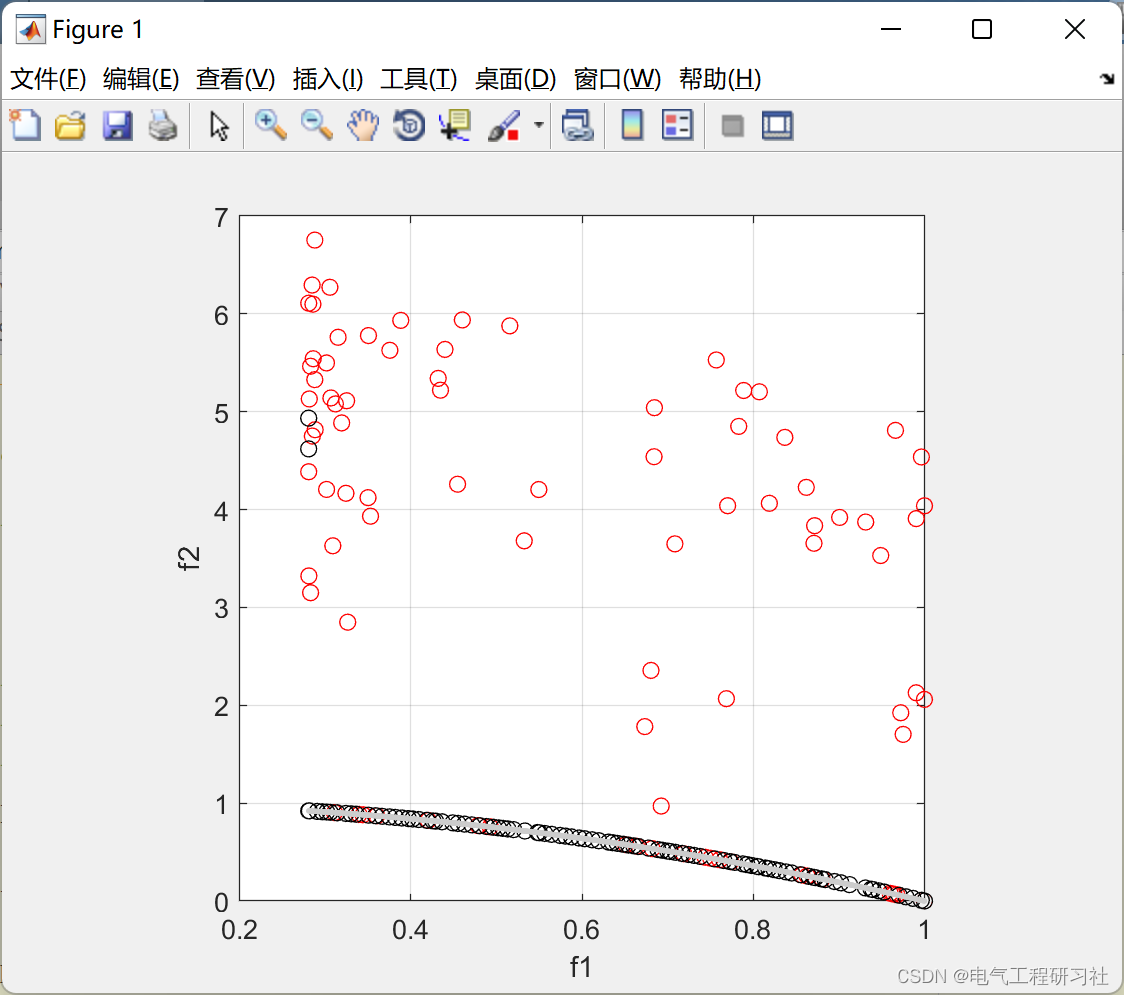
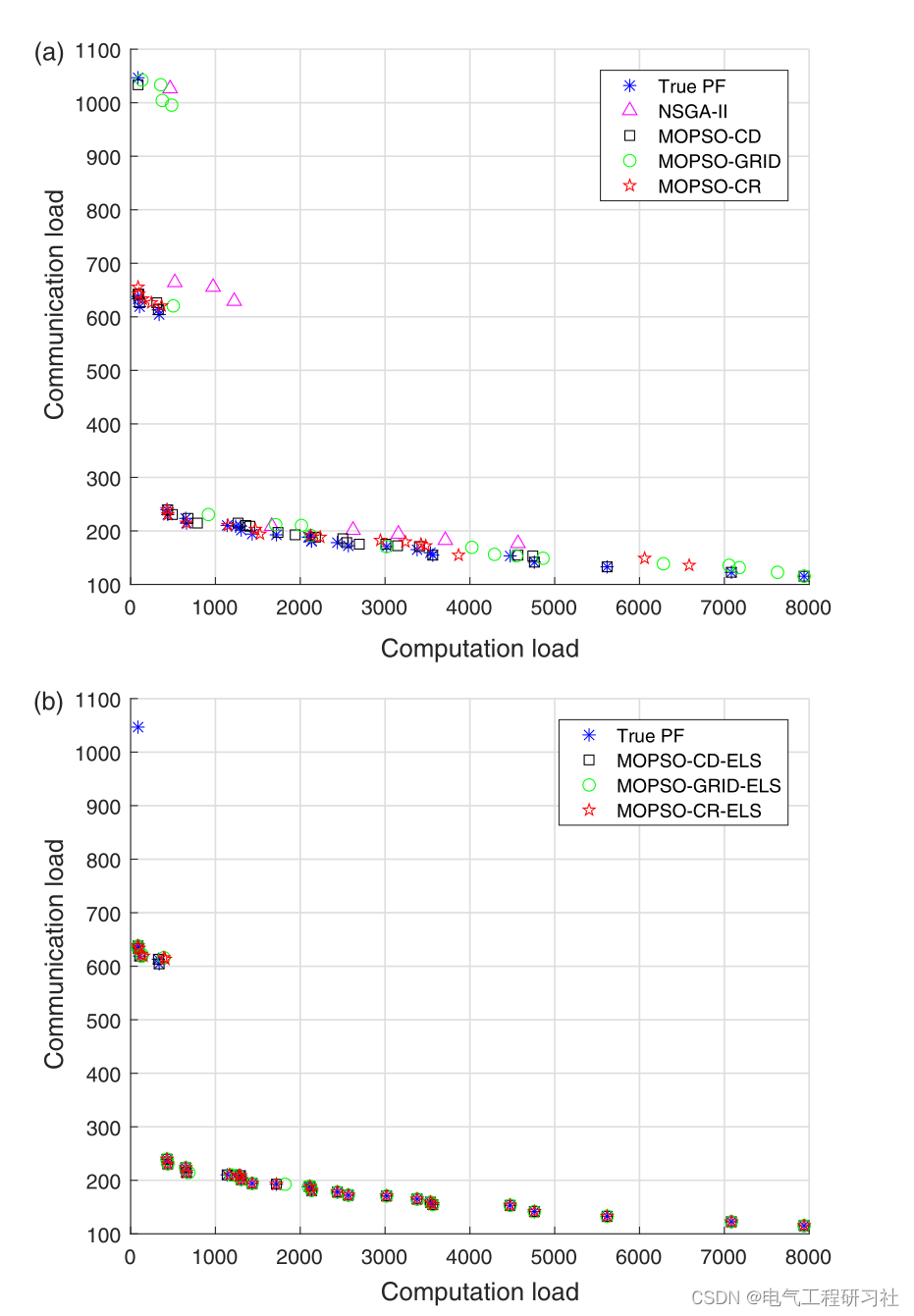
部分代码:
function REP = MOPSOCD(params,MultiObj)
%% 参数
Np = params.Np;
Nr = params.Nr;
maxgen = params.maxgen;
W = params.W;
C1 = params.C1;
C2 = params.C2;
%ngrid = params.ngrid;
maxvel = params.maxvel;
%u_mut = params.u_mut;
fun = MultiObj.fun;
nVar = MultiObj.nVar;
var_min = MultiObj.var_min(:);
var_max = MultiObj.var_max(:);
d=nVar; %搜索空间维数(未知数个数)
xmin=var_min;
xmax=var_max;
xrange=xmax-xmin;
n=Np; %初始化群体个体数目
MaxDT=maxgen; %最大迭代次数
rp=[]; %外部存档,档案里存的是每代保存下来的非支配解,也是算法求解的结果
rpmax=Nr; %档案规模
c1=C1;c2=C2;
w=W; %惯性权重
% pbx n*d 矩阵---个体最优解
% gbx n*d 矩阵---全局最优解(每个粒子的全局最优解都不同)
% pbf n*k 矩阵----个体最优值
% gbf n*k 矩阵----全局最优值
%产生随机 n 个粒子,初始化粒子的位置和速度
%x=xmin+xrange.*rand(n,d);
x=[];
for i=1:n
x(i,:)=xmin'+xrange'.*rand(1,d);
end
v=zeros(n,d);
maxvel = (var_max-var_min).*maxvel./100;
tmp = fun(x);
%% 计算粒子的适应度
k=size(tmp,2); %目标函数个数
x(:,2*d+1:2*d+k)=tmp;
x(:,d+1:2*d)=v;
%% 求个体极值和全局极值
pbx=x(:,1:d); %个体最优位置为初始粒子本身
pbf=x(:,2*d+1:2*d+k);
gbx=x(:,1:d); %全局最优位置为初始粒子本身
gbf=x(:,2*d+1:2*d+k);
xk=x(:,1:d);
v=x(:,(d+1):2*d);
rp = x;
%% 可视化
if(k==2)
h_fig = figure(1);
h_par = plot(x(:,2*d+1),x(:,2*d+2),'or'); hold on;
h_rep = plot(rp(:,2*d+1),rp(:,2*d+2),'ok'); hold on;
try
set(gca,'xtick',REP.hypercube_limits(:,1)','ytick',REP.hypercube_limits(:,2)');
axis([min(REP.hypercube_limits(:,1)) max(REP.hypercube_limits(:,1)) ...
min(REP.hypercube_limits(:,2)) max(REP.hypercube_limits(:,2))]);
grid on; xlabel('f1'); ylabel('f2');
end
drawnow;
end
if(k==3)
h_fig = figure(1);
h_par = plot3(POS_fit(:,1),POS_fit(:,2),POS_fit(:,3),'or'); hold on;
h_rep = plot3(REP.pos_fit(:,1),REP.pos_fit(:,2),REP.pos_fit(:,3),'ok'); hold on;
try
set(gca,'xtick',REP.hypercube_limits(:,1)','ytick',REP.hypercube_limits(:,2)','ztick',REP.hypercube_limits(:,3)');
axis([min(REP.hypercube_limits(:,1)) max(REP.hypercube_limits(:,1)) ...
min(REP.hypercube_limits(:,2)) max(REP.hypercube_limits(:,2))]);
end
grid on; xlabel('f1'); ylabel('f2'); zlabel('f3');
drawnow;
axis square;
end
display(['Generation 0 - Repository size: ' num2str(size(rp,1))]);
%开始循环
for t=1:MaxDT
%根据粒子群公式迭代,位置、速度更新
gen = t;
for i=1:n
%v(i,:)=0.3.*randn(1,d)+c1.*rand.*(pbx(i,:)-xk(i,:))+c2.*rand.*(gbx(i,:)-xk(i,:));
v(i,:)=w.*v(i,:)+c1.*rand.*(pbx(i,:)-xk(i,:))+c2.*rand.*(gbx(i,:)-xk(i,:));
for j=1:d
if v(i,j)>maxvel(j)
v(i,j)=maxvel(j);
elseif v(i,j)<-maxvel(j)
v(i,j)=-maxvel(j);
end
end
xk(i,:)=xk(i,:)+v(i,:);
for j=1:d
if xk(i,j)>xmax(j)
xk(i,j)=xmax(j);
elseif xk(i,j)<xmin(j)
xk(i,j)=xmin(j);
end
end
end
for i=1:n
mu=0.1; % Mutation Rate
pm=(1-(t-1)/(MaxDT-1))^(1/mu);
if rand<pm
xk(i,:) = Mutate(xk(i,:),pm,xmin,xmax);
end
for j=1:d
if xk(i,j)>xmax(j)
xk(i,j)=xmax(j);
elseif xk(i,j)<xmin(j)
xk(i,j)=xmin(j);
end
end
end
x(:,1:d)=xk;
x(:,(d+1):2*d)=v;
%计算粒子的适应度
x(:,2*d+1:2*d+k)=fun(xk);
%求非支配解集 np(快速排序法)
q=x;np=[];
while isempty(q)==0
xsb=q(1,:);
q(1,:)=[];
flag=1; %若 flag==1,则 xsb 是非支配解,就可以放到非支配解集中了
[column,row]=size(q);
for i=1:column
dom_less=0;
dom_equal=0;
dom_more=0;
for l=1:k
if xsb(2*d+l)<q(i,2*d+l)
dom_less=dom_less+1;
elseif xsb(2*d+l)==q(i,2*d+l)
dom_equal=dom_equal+1;
else
dom_more=dom_more+1;
end
end
%若 xsb 支配 q(i),则将 q(i)所在的行标记为 0,用来到最后删除此行做标记
if dom_more==0&dom_equal~=k
q(i,:)=0;
%若 q(i)支配 xsb,那么 xsb 不是非支配解,不能被放入非支配解集
elseif dom_less==0&dom_equal~=k
flag=0;break
end
end
if flag==1 %若 xsb 是非支配解,则将其放入非支配解集 np 中
np=[np;xsb];
end
%将 q 中标记为 0 的行删除,剩下不被 xsb 支配的粒子,即快速排序的简便之处
q(~any(q,2),:)=[];
end
%更新个体极值(若当前位置支配其个体极值位置,则更新为当前位置)
for i=1:n
dom_less=0;
dom_equal=0;
dom_more=0;
for l=1:k
if x(i,2*d+l)<pbf(i,l)
dom_less=dom_less+1;
elseif x(i,2*d+l)==pbf(i,l)
dom_equal=dom_equal+1;
else
dom_more=dom_more+1;
end
end
if dom_more==0&dom_equal~=k
pbf(i,:)=x(i,2*d+1:2*d+k);
pbx(i,:)=x(i,1:d);
end
end
%更新外部集 rp(将非支配集按支配关系插入外部集)
[column,row]=size(rp);
if column==0
rp=np;
else
[column2,row2]=size(np);
for i=1:column2
flag=1; %若 flag==1,则 np(i,:)是就可以放到外部集中了
[column1,row1]=size(rp);
for j=1:column1
dom_less=0;
dom_equal=0;
dom_more=0;
for l=1:k
if np(i,2*d+l)<rp(j,2*d+l)
dom_less=dom_less+1;
elseif np(i,2*d+l)==rp(j,2*d+l)
dom_equal=dom_equal+1;
else
dom_more=dom_more+1;
end
end
%若非支配集中的粒子 np(i,:)支配外部集中的粒子 rp(j,:),
%则将 rp(j,:)所在的行标记为 0,用来到最后删除此行做标记
if dom_more==0&dom_equal~=k
rp(j,:)=0;
%若 rp(j,:)支配 np(i,:),则表示 np(i,:)被 rp(j,:)支配,
%那么 np(i,:)就一定不是非支配解,就不能被放入非支配解集中了
elseif dom_less==0&dom_equal~=k
flag=0;break
end
end
if flag==1 %若 flag==1,则 np(i,:)是就可以放到外部集中了
rp=[rp;np(i,:)];
end
rp(~any(rp,2),:)=[];
end
end
np = rp;
[column,row]=size(rp);
for i=1:column
for j=i:column
if i~=j && sum(np(i,1:d)-np(j,1:d) == 0) == d
rp(i,:)=0;
break;
end
end
end
rp(~any(rp,2),:)=[];
%基于拥挤距离控制档案规模
%(计算外部集中粒子的拥挤距离,对拥挤距离进行降序排序,删除后面的多余个体)
[column,row]=size(rp);
indexrp=[1:column]';
rp=[rp indexrp]; %索引
rp(:,2*d+k+2)=zeros(column,1); %用来保存拥挤距离
for i=1:k
rp=sortrows(rp,2*d+i); %将粒子进行对第 i 个目标函数值进行升序排列
if column>2
for j=2:column-1
rp(j,2*d+k+2)= rp(j,2*d+k+2)+(rp(j+1,2*d+i)-rp(j-1,2*d+i))/(rp(column,2*d+i)-rp(1,2*d+i));
end
end
rp(1,2*d+k+2)=rp(1,2*d+k+2)+inf;
rp(column,2*d+k+2)=rp(column,2*d+k+2)+inf;
end
rp=sortrows(rp,-(2*d+k+2)); %外部集根据拥挤距离降序排序
if column>rpmax
rp=rp(1:rpmax,:);
end
%更新全局极值(此时外部集已根据拥挤距离降序排序,从外部集的最前部分随机选择)
for i=1:n
%产生一个随机数,从外部集前 10%的粒子里面选
randomnumber=ceil(rand*column/10);
gbx(i,:)=rp(randomnumber,1:d); %全局最优位置
gbf(i,:)=rp(randomnumber,2*d+1:2*d+k);
end
rp(:,2*d+k+1:2*d+k+2)=[];
% Plotting and verbose
if(k==2)
figure(h_fig); delete(h_par); delete(h_rep);
h_par = plot(x(:,2*d+1),x(:,2*d+2),'or'); hold on;
h_rep = plot(rp(:,2*d+1),rp(:,2*d+2),'ok'); hold on;
try
set(gca,'xtick',REP.hypercube_limits(:,1)','ytick',REP.hypercube_limits(:,2)');
axis([min(REP.hypercube_limits(:,1)) max(REP.hypercube_limits(:,1)) ...
min(REP.hypercube_limits(:,2)) max(REP.hypercube_limits(:,2))]);
end
if(isfield(MultiObj,'truePF'))
try delete(h_pf); end
h_pf = plot(MultiObj.truePF(:,1),MultiObj.truePF(:,2),'.','color',0.8.*ones(1,3)); hold on;
end
grid on; xlabel('f1'); ylabel('f2');
drawnow;
axis square;
end
if(k==3)% 以后再改
figure(h_fig); delete(h_par); delete(h_rep);
h_par = plot3(POS_fit(:,1),POS_fit(:,2),POS_fit(:,3),'or'); hold on;
h_rep = plot3(REP.pos_fit(:,1),REP.pos_fit(:,2),REP.pos_fit(:,3),'ok'); hold on;
try
set(gca,'xtick',REP.hypercube_limits(:,1)','ytick',REP.hypercube_limits(:,2)','ztick',REP.hypercube_limits(:,3)');
axis([min(REP.hypercube_limits(:,1)) max(REP.hypercube_limits(:,1)) ...
min(REP.hypercube_limits(:,2)) max(REP.hypercube_limits(:,2)) ...
min(REP.hypercube_limits(:,3)) max(REP.hypercube_limits(:,3))]);
end
if(isfield(MultiObj,'truePF'))
try delete(h_pf); end
h_pf = plot3(MultiObj.truePF(:,1),MultiObj.truePF(:,2),MultiObj.truePF(:,3),'.','color',0.8.*ones(1,3)); hold on;
end
grid on; xlabel('f1'); ylabel('f2'); zlabel('f3');
drawnow;
axis square;
end
display(['Generation #' num2str(gen) ' - Repository size: ' num2str(size(rp,1))]);
end
REP.pos = rp(:,1:d);
REP.pos_fit = rp(:,2*d+1:2*d+k);
hold off;
% hold on;
% rpcd=rp;
% plot(rpcd(:,2*d+1),rpcd(:,2*d+2),'^');
end
function xnew=Mutate(x,pm,VarMin,VarMax)
nVar=numel(x);
j=randi([1 nVar]);
dx=pm*(VarMax(j)-VarMin(j));
lb=x(j)-dx;
ub=x(j)+dx;
lb = max(lb,VarMin(j));
lb = min(lb,VarMax(j));
ub = max(ub,VarMin(j));
ub = min(ub,VarMax(j));
xnew=x;
xnew(j)=unifrnd(lb,ub);
end
5 Matlab代码+数据+文档讲解
博客主页:电气辅导帮









![[Java] HashMap是如何实现的?扩容机制是什么?树化机制知道吗?结合源码带你理解HashMap的原理。](https://img-blog.csdnimg.cn/d11b725533394f57a8c5a894b7cc560c.png)