目录
1.算法描述
2.仿真效果预览
3.MATLAB核心程序
4.完整MATLAB
1.算法描述
所谓信道估计,就是从接收数据中将假定的某个信道模型的模型参数出来的过程。如果信道是线性的话,那么信道估计就是对系统冲激响应进行估计。
CS-OMP
正则正交匹配追踪(Regularized OMP)算法在超宽带系统信道估计中的应用。OMP算法在应用于稀疏信号恢复时,具备贪婪算法计算速度快和计算复杂度低的特点。超宽带通信(UWB)系统的信道估计需要估计一组最大径的参数,而OMP具有能够可靠恢复近似稀疏含噪信号的能力,适用于UWB信道估计。
假设需要重构信号x,现可将信号x抽象为RN空间的N×1维列向量,在RN空间中,任何信号均可以使用N×1的规范正交基向量:

∈RN为投影系数,但仅有K个非零元素(K<<N),此时是N维—K稀疏向量。在重构信号x时,仅需估计K个未知参数而不是N个实际的未知参数,从而大大减少了采样信号的量,同时可以恢复原信号x。在CS理论中,对需要重构的信号x的采样,实际上是利用M×N的矩阵的M个行向量对投影系数向量的一个线性投影过程。信号x经过线性变换后,输出的观测信号y包含M个参数,每一个参数均为信号x的一个观测量,即:
在LS估计中,我们使用Y和Y‘’来进行计算,估计出的结果是H’而并非H,若估计的结果H’使得Y’与Y误差最小,则能得到的结果应该是H’与H(带三角)的误差最小,但H(带三角)也不是真实的信道矩阵,其内还包含了一个误差项Z/X,因此对于LS信道估计而言,其结果的精度是受这个误差项影响的,而这个误差项概括来说就是和SNR相关,SNR越大,误差项越小,LS估计精度越高。现依据LS最优准则对上式中H’进行估计,首先给出LS准则的代价函数。
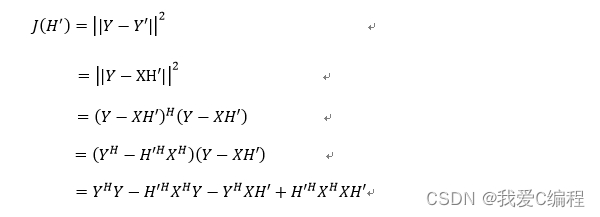
MMSE
依旧是给出假定的信号关系式
Y为接收数据(包含多径)大小为Nx1。
X为先验信息,大小为NXM。
h为信道冲激响应,大小为MX1。
Z为噪声,大小为NX1。
MMSE信道估计的代价函数为
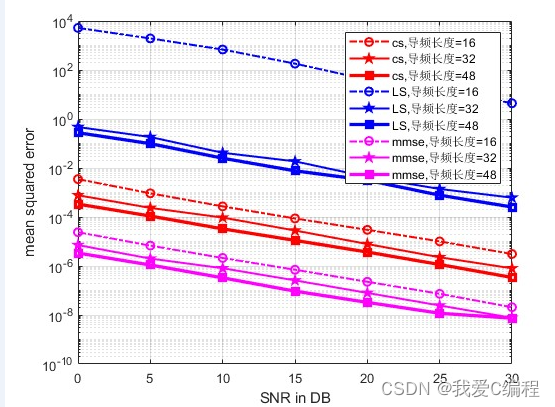
2.仿真效果预览
matlab2022a仿真结果如下:
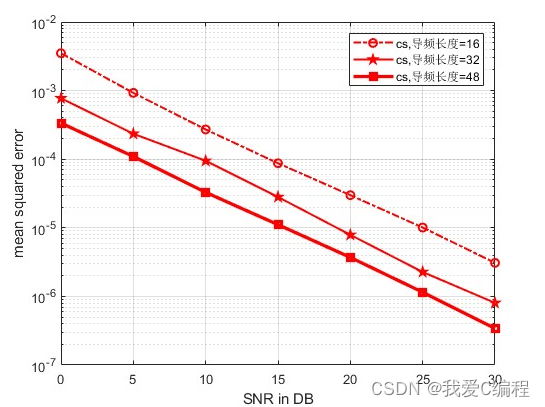
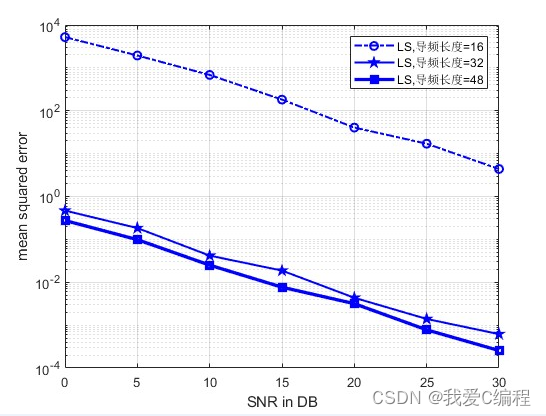

3.MATLAB核心程序
%频域信道估计
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
rng('default');
L1=31;
taps=6;%抽头数
K=taps;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---------------------------频域的信道脉冲响应----------------------%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
SNR = [0:5:30];
LEN = length(SNR);
l1=channel(L1,taps);
l2=channel(L1,taps);
h=cat(2,l1,l2)';
L=size(h,1);
cs=zeros(3,LEN);
ls=zeros(3,LEN);
mmse=zeros(3,LEN);
for t=1:3
N1=16*t;%训练序列长度
N=N1*20;
[cs_mse_ave,ls_mse_ave,mmse_mse_ave]=MSE_com(N,L,K,h,N1);
cs(t,:)=cs_mse_ave;
ls(t,:)=ls_mse_ave;
mmse(t,:)=mmse_mse_ave;
end
A1134.完整MATLAB
V



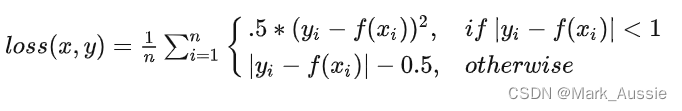


![[Java] HashMap是如何实现的?扩容机制是什么?树化机制知道吗?结合源码带你理解HashMap的原理。](https://img-blog.csdnimg.cn/d11b725533394f57a8c5a894b7cc560c.png)