关于报告的所有内容，公众【营销人星球】获取下载查看

核心观点

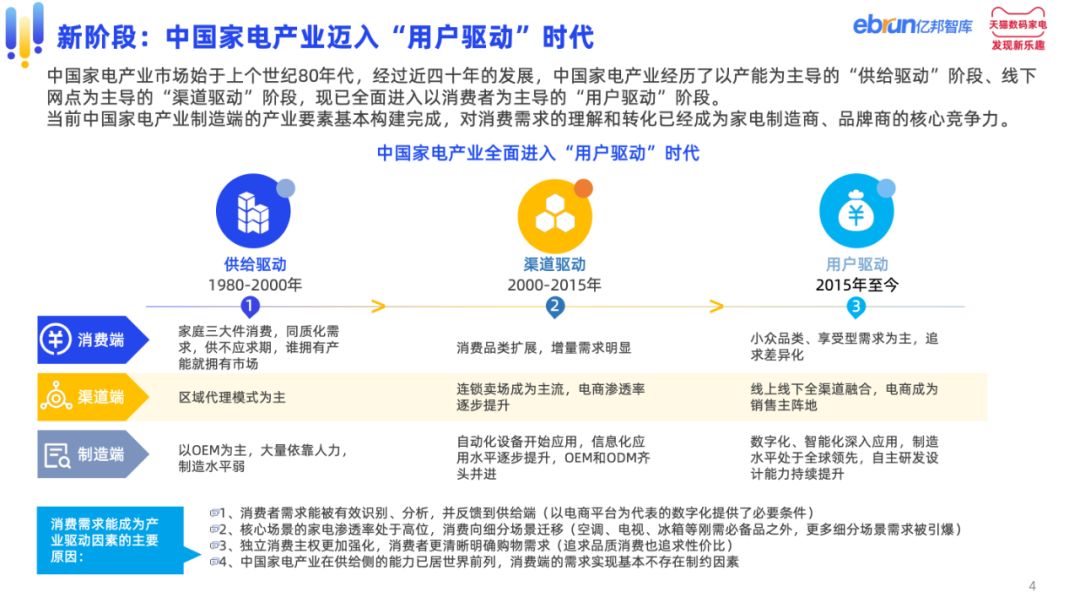
中国家电产业市场始于上个世纪80年代，经过近四十年的发展，中国家电产业经历了以产能为主导的“供给驱动〞 阶段、线下网点为主导的“溪道驱动”阶段，现已全面进入以消费者为主导的“用户驱动〞阶段。

当前中国家电产业制造端的产业要素基本构建完成，对消费需求的理解和转化已经成为家电制造商、品牌商的核心竞争力。

报告来源

免责声明：营销人星球尊重知识产权、数据隐私，只做内容的收集、整理及分享，报告内容来源于网络,报告版权归原撰写发布机构所有，通过公开合法渠道获得，如涉及侵权，请及时联系我们删除；如对报告内容存疑，请与撰写、发布机构联系。