整数规划——第三章 全单模矩阵

若线性规划问题的约束矩阵为全单模矩阵，则该问题可行域的顶点都是整数点，从而线性规划与整数规划的最优解相同。

3.1 全单模性与最优性

考虑线性整数规划问题：
$$\text{(IP)}\begin{array}{rl}& \min c^{T}x,\\ & s.t.Ax\le b,\\ & x\in {\mathbb{Z}}_{+}^n\end{array}$$
其中 $A$ 是 $m\times n$ 整数矩阵，$b$ 是 $n$ 维整数向量。用如下线性规划作为其松弛问题：
$$\text{(LP)}\begin{array}{rl}& \min c^{T}x,\\ & s.t.Ax\le b,\\ & x\in {\mathbb{R}}_{+}^n\end{array}$$
若线性松弛问题存在最优解，且其可行集合 $P={x\in \R_+^n|Ax\le b}
$ 的所有顶点都是整数点，则线性规划问题必有整数最优解。因此，求解线性松弛问题(LP)就可得到原整数规划问题§的最优解。下面给出一个保证问题(LP)的最优解是整数点的充分条件

定理3.1 若线性规划问题(LP)的最优基矩阵B满足 $\text{det}(B)=\pm 1$，这里 $B$ 是矩阵 $(A,I)$ 的$m\times m$ 维子方阵，则线性规划问题(LP)的最优解是整数解。

定义3.1 设矩阵 $A$ 是 $m\times n$ 整数矩阵。若矩阵 $A$ 的任意子方阵的行列式等于0,1或者-1，则称矩阵A为全单模矩阵。

易知，若整数规划（IP）中的矩阵 $A$ 是全单模矩阵，求解线性规划（LP）等价于求解整数规划（IP)。

性质3.1若矩阵 $A$ 是全单模矩阵，则矩阵中元素a=0,1或者-1。

定理3.2 设矩阵 $A$ 是全单模矩阵，向量 $b$ 是整数向量，则多面体 P = { x ∈ R + n ∣ A x ≤ b } P=\{x\in \R_+^n|Ax\le b\} P={x∈R+n​∣Ax≤b} 的顶点都是整数点。

定理3.3 若对任意整数向量 $b$ ，多面体 P = { x ∈ R + n ∣ A x ≤ b } P=\{x\in \R_+^n|Ax\le b\} P={x∈R+n​∣Ax≤b} 的顶点都是整数点，则 $A$ 是全单模矩阵。

3.2 全单模矩阵的性质

性质3.2 设整数矩阵 $A$ 是全单模矩阵，对 $A$ 进行以下运算不改变其全单模性：

1. 对矩阵 $A$ 进行转置；
2. 矩阵 $(A,I)$ 是全单模的；
3. 去掉 $A$ 的一行（或者一列)：
4. 将 $A$ 的一行（或者一列）乘以-1；
5. 互换 $A$ 的两行（或者两列）：
6. 对 $A$ 进行转轴运算.

定理3.4 矩阵 $A$ 是全单模矩阵等价于对于每个集合 J ⊆ N = { 1 , 2 , . . . , n } J\sube N=\{1,2,...,n\} J⊆N={1,2,...,n}，必存在 $J$ 的分割 $J_1,J_2$ 使得
$$\left|\sum _{j\in J_1}{a}_{ij}-\sum _{j\in J_2}{a}_{ij}\right|\le 1,i=1,...,m.$$
推论3.3 设矩阵 $A$ 是 { 0 , 1 , − 1 } \{0,1,-1\} {0,1,−1}矩阵，并且每列至多有两个非零元素，则矩阵 $A$ 是全单模矩阵当且仅当存在 $A$ 的行分割 $Q_1,Q_2$ 使得同一列中的两个非零元素满足以下条件：

1. 若符号相同，则一个元素位于 $Q_1$,另一元素位于 $Q_2$
2. 若特号相反，则这两个元素同时属于 $Q_1$,或者同时属于 $Q_2$。

由以上讨论可得到一个易于验证的全单模矩阵的充分条件

推论3.4 设矩阵 $A$ 的任意元素都是0,1或者一1，若 $A$ 满足以下两个条件，则矩阵 $A$ 是全单模的：

1. $A$ 的每一列至多含有两个非零元素；
2. 若某列含有两个非零元素，则两个元素之和为0.

3.3 全单模矩阵在网络问题中的应用

3.3.1 二部图

给定无向图 $G=(V,E)$，其中 $V$ 表示顶点集合，$E$ 表示边集合。定义图 $G$ 的关联矩阵$M$ ，其行和列分别用顶点集 $V$ 和边集 $E$ 标记；若边 $e$ 经过项点 $v$ ,则 $M_{v,e}=1$；否则 $M_{v,e}=0$。

若一个图 $G=(V,E)$ 的顶点集合 $V$ 可分解成两个非空子集 $V_1,V_2$，使得 $E$ 中每条边的两个端点分别属于 $V_1,V_2$，则称该图为二部图。下面定理表明无向图的关联矩阵的全单模性与二部图之间的等价性。

定理3.5 令 $G=(V,E)$ 表示无向图，$M$ 表示图 $G$ 的 $V\times E$ 关联矩阵，则 $M$ 是全单模矩阵当且仅当图 $G$ 是二部图。

3.3.2 指派问题

指派问题是二部图问题的一种特殊情况，是指将 $n$ 项任务恰当地分配给 $n$ 个工人，每个工人只能执行一项任务。由于每个工人完成不同工作所的成本不同，我们的目的是在保证各项任务完成的前提下最小化成本。令表示 $c_{ij}$ 由工人 $i$ 完成任务 $j$ 的成本，则最小化成本的指派问题可表述如下：
min ⁡ ∑ i = 1 n ∑ j = 1 n c i j x i j , s . t .   ∑ j = 1 n x i j = 1 ,   i = 1 , . . . , n , ∑ i = 1 n x i j = 1 , j = 1 , . . . , n , x i j ∈ { 0 , 1 } , i , j = 1 , . . . , n . \begin{aligned}&\min \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij},\\ &s.t.\ \sum_{j=1}^nx_{ij} =1,\ i = 1,...,n,\\ &\quad\quad\sum_{i = 1}^n x_{ij} =1,j=1,...,n, \\ &\quad\quad x_{ij}\in \{0,1\},\quad i,j = 1,...,n. \end{aligned} ​mini=1∑n​j=1∑n​cij​xij​,s.t. j=1∑n​xij​=1, i=1,...,n,i=1∑n​xij​=1,j=1,...,n,xij​∈{0,1},i,j=1,...,n.​
记 $U$ 表示工人集合，$V$ 表示任务集合，在此集合上建立边集$E$：若工人 $i$ 能够胜任任务 $j$ ,则边 $(i,j)\in E$ 。故图 $G=(U,V,E)$ 是二部图。由于二部图的关联矩阵是全单模矩阵，则求解其线性规划松弛问题即可得到整数最优解.，

另一类指派问题是将工人们分派到不同小组进行轮班，称之为排班问题。假设工作时间有 $m$ 个小时，共有 $n$ 次轮班，每一次轮班需要连续工作几个小时。第 $j$ 次轮班用 $m$ 维 $0-1$ 向量 $a_j$ 表示：若在第 $i$ 个小时被排在第 $j$ 次轮班中，则 $a_{ij}=1$ ；否则 $a_{ij}=0$ 。所以向量 中 1 元素是连续出现的，实际上。由 $a_j,j=1,...n$ 组成的矩阵 $A$ 是 $m\times n$ 维的区间矩阵。区间矩阵定义如下，其具有全单模性：

定义3.2 设 $A$ 是 $m\times n$ 维 { 0 , 1 } \{0,1\} {0,1} 矩阵，若该矩阵的每一列中 $1$ 元素连续出现，即如果 $a_{ij}=a_{kj}=1$，且 $k>i+1$，那么对任意 $i<l<k,a_{lj}=1$，则称 $A$ 为区间矩阵。

定理3.6 区间矩阵是全单模矩阵。

所以求解上述问题的线性规划松弛即可得到整数最优解。

3.3.3 最小费用网络流问题

有向图关联矩阵介绍如下：

给定有向图 $D=(V,A)$，$V$ 表示顶点集，$A$ 表示弧的集合，$(u,v)\in A$ 表示从顶点 $u$ 流向顶点 $v$ 的弧.记其 $V\times A$ 相关矩阵为 $M$ 。若弧 $a$ 流入顶点 $v$，则 $M_{v,a}=1$；若弧 $a$ 流出顶点 $v$，则 $M_{v,a}=-1$；否则 $M_{v,a}=0$。

定理3.7 有向图 $D=(V,A)$的关联矩阵 $M$ 是全单模矩阵.

给定有向图 $D=(V,A)$ ，$h_{u,v}$ 表示弧 $(u,v)$ 上的最大容量，$b_v$ 表示顶点 $v$ 处的需求量，$c_{u,v}$ 表示弧 $(u,v)$ 上单位流量所需要的费用，记
V + ( v ) = { u ∈ V ∣ ( v , u ) ∈ A } , V − ( v ) = { u ∈ V ∣ ( u , v ) ∈ A } V^+(v)=\{u\in V|(v,u)\in A\},\quad V^-(v)=\{u\in V|(u,v)\in A\} V+(v)={u∈V∣(v,u)∈A},V−(v)={u∈V∣(u,v)∈A}
则最小费用网络流问题可以表述为
$$\begin{array}{rl}& \min \sum _{(u,v)\in A}{c}_{u,v}{x}_{u,v},\\ & s.t.\sum _{u\in V^{+}(v)}{x}_{v,u}-\sum _{u\in V^{-}(v)}{x}_{u,v}=b_v,\forall v\in V,\\ & 0\le x_{u,v}\le h_{u,v},\forall (u,v)\in A\end{array}$$

最小费用网络流问题的输入是一个有向图，其中每条边都有一个容量和一个单位流量费用。该图还有一个源点和一个汇点。问题的目标是在满足源点到汇点之间流量约束的情况下，找到一种最小费用的流量分配方案。

记 $M$ 为该图的关联矩阵。上述最小费用网络流问题即
min ⁡ { c T x ∣ M x = b ,   0 ≤ x ≤ h } \min \{c^Tx|Mx=b,\ 0\le x \le h\} min{cTx∣Mx=b, 0≤x≤h}
应当注意的是，若该问题可行，则总需求量之和必为0，即 ${\sum }_{v\in V}{b}_v=0$。若容 $h_{u,v}$ 及各顶点需求量 $b_v$ 都是整数，由关联矩阵 $M$ 的全单模性可知该最小费用网络流问题有整数最优解。

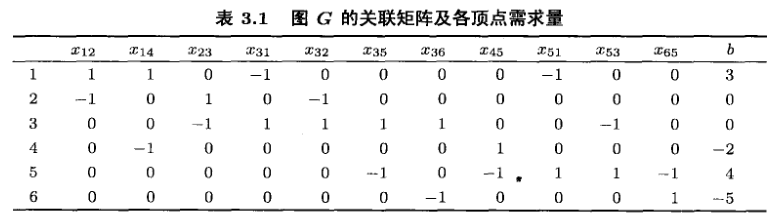
例3.2 有向图 $G$ 由图3.1给出，图 $G$ 的关联矩阵和各顶点需求量由表3.1给出