C语言基础知识点一：
1.数据类型
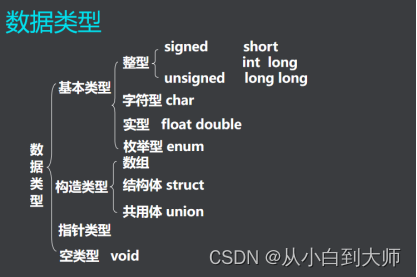
2.bool类型：
使用bool时时，需要增加<stdbool.h>头文件。
说明：bool 类型只有非零（true）和零（false）两种值。
如: if（-1）x=12;else x=18;
-1为非零值，所以x为12
3.数据长度与值域：
（1）char类型
使用char数据类型的变量需要特别注意，防止数据超出值域
eg: char c1=128; 错误，超出值域
unsigned char c2=-1; 错误 超出值域
char 与signed char 值域范围为**-128~127之间
unsigned char 值域范围为0~255**
char与unsigende char类型长度为1个字节长度。
（2）short类型
short 类型值域为-32768~32767之间
unsigned short 类型的值域为0~65536
short 与unsigned short 长度为2个字节
(3)int类型
