一、说明

        我遇到了一些关于降维技术的资源。这个主题绝对是最有趣的主题之一，很高兴认为有一些算法能够通过选择仍然代表整个数据集的最重要的特征来减少特征的数量。作者指出的优点之一是这些算法可以改善分类任务的结果。

        在这篇文章中，我将使用主成分分析（PCA）来验证这个陈述，以尝试提高神经网络在数据集上的分类性能。PCA 真的能改善分类结果吗？一起来看看吧。

二、关于降维算法

        在直接开始编写代码之前，让我们先谈谈降维算法。降维有两种主要算法：线性判别分析（LDA）和主成分分析（PCA）。这两者之间的基本区别在于，LDA使用类的信息来查找新特征，以最大化其可分离性，而PCA使用每个特征的方差来做同样的事情。在这种情况下，LDA可以被认为是一种监督算法，而PCA是一种无监督算法。

2.1 谈论PCA

        PCA 背后的想法只是找到一组汇总数据的低维轴。为什么我们需要汇总数据？让我们考虑一下这个例子：我们有一个由一组来自汽车的属性组成的数据集。这些属性通过尺寸、颜色、圆度、紧凑性、半径、座位数、门数、后备箱尺寸等来描述每辆车。但是，其中许多特征将测量相关属性，因此将是多余的。因此，我们应该消除这些冗余，并描述每辆车的属性较少。这正是PCA的目标。例如，将车轮数量视为汽车和公共汽车的一个特征，几乎两个类的每个示例都有四个轮子，因此我们可以说这个特征的方差很小（在一些罕见的公共汽车中从四个到六个轮子或更多），所以这个特征将使公共汽车和汽车看起来一样， 但它们实际上彼此非常不同。现在，将高度视为一个特征，汽车和公共汽车有不同的值，方差的范围很大，从最低的汽车到最高的公共汽车。显然，这些车辆的高度是将它们分开的良好属性。回想一下，PCA不考虑类的信息，它只查看每个特征的方差，因为合理地假设具有高方差的特征更有可能在类之间具有良好的划分。

        通常，人们最终会错误地认为PCA从数据集中选择某些特征并丢弃其他特征。该算法实际上基于旧属性的组合构建新的属性集。从数学上讲，PCA执行线性变换，将原始特征集移动到由主成分组成的新空间。这些新特征对我们来说没有任何真正的意义，只有代数，因此不要认为结合线性特征，你会发现你从未想过它会存在的新功能。许多人仍然相信机器学习算法是神奇的，他们直接将数千个输入输入到算法中，并希望为他们的业务找到所有见解和解决方案。不要被欺骗。数据科学家的工作是通过使用机器学习算法作为一组工具而不是魔杖，通过对数据进行良好的探索性分析来定位对业务的见解。请记住这一点。

2.2 主成分空间是什么样的？

        在新的功能空间中，我们正在寻找一些在类之间差异很大的属性。正如我在前面的例子中所展示的，一些呈现低方差的属性是没有用的，这将使示例看起来相同。另一方面，PCA 查找在类之间显示尽可能多的变化的属性，以构建主组件空间。该算法使用方差矩阵、协方差矩阵、特征向量和特征值对的概念来执行 PCA，从而提供一组特征向量及其各自的特征值。PCA的确切表现是下一篇文章的材料。

        那么，我们应该如何处理特征值和特征向量呢？这很简单，特征向量表示主成分空间的新轴集，特征值携带每个特征向量具有的方差量信息。因此，为了减小数据集的维度，我们将选择那些方差较大的特征向量，并丢弃方差较小的特征向量。当我们浏览下面的示例时，它将越来越清楚它是如何工作的。

2.3 让我们最后看到一些代码。

        现在，我们到达了这篇文章的有趣和有趣的部分。让我们看看 PCA 是否真的改善了分类任务的结果。

        为了证明这一点，我的策略是在数据集上应用神经网络并查看其初始结果。之后，我将在分类之前执行 PCA，并在新数据集上应用相同的神经网络，最后比较两个结果。

        该数据集源自UCI机器学习存储库，称为“Statlog（车辆轮廓）数据集”。此数据集存储了四辆车轮廓的一些度量，用于分类。它由946个示例和18个度量（属性）所有数值组成，您可以在此链接中查看更多详细信息：https://archive.ics.uci.edu/ml/datasets/Statlog+（车辆+轮廓）。神经网络将是一个具有四个隐藏节点和一个输出节点的多层感知器，所有节点都具有sigmoid函数作为激活函数，PCA函数将来自R包。

2.4 准备数据集

        首先，我将为二元分类准备数据集。

        我将仅从两个类中选择示例，以构成二元分类。这些示例将来自“bus”和“saab”类。类“saab”将被类 0 取代，类“总线”将被类 1 取代。下一步包括将数据集分为训练数据集和测试数据集，分别占总类示例的 60% 和 40%。

        在前面的数据集准备之后，让我们一次使用所有特征对神经网络进行建模，然后应用测试数据集。

# Load library
library( dplyr )

# Load dataset
data = read.csv( "../dataset/vehicle.csv", stringsAsFactor = FALSE )

# Transform dataset
dataset = data %>% 
            filter( class == "bus" | class == "saab" ) %>%
            transform( class = ifelse( class == "saab", 0, 1 ) )
dataset = as.data.frame( sapply( dataset, as.numeric ) )

# Spliting training and testing dataset
index = sample( 1:nrow( dataset ), nrow( dataset ) * 0.6, replace = FALSE ) 

trainset = dataset[ index, ]
test = dataset[ -index, ]
testset = test %>% select( -class )

# Building a neural network (NN)
library( neuralnet )
n = names( trainset )
f = as.formula( paste( "class ~", paste( n[!n %in% "class"], collapse = "+" ) ) )
nn = neuralnet( f, trainset, hidden = 4, linear.output = FALSE, threshold = 0.01 )

plot( nn, rep = "best" )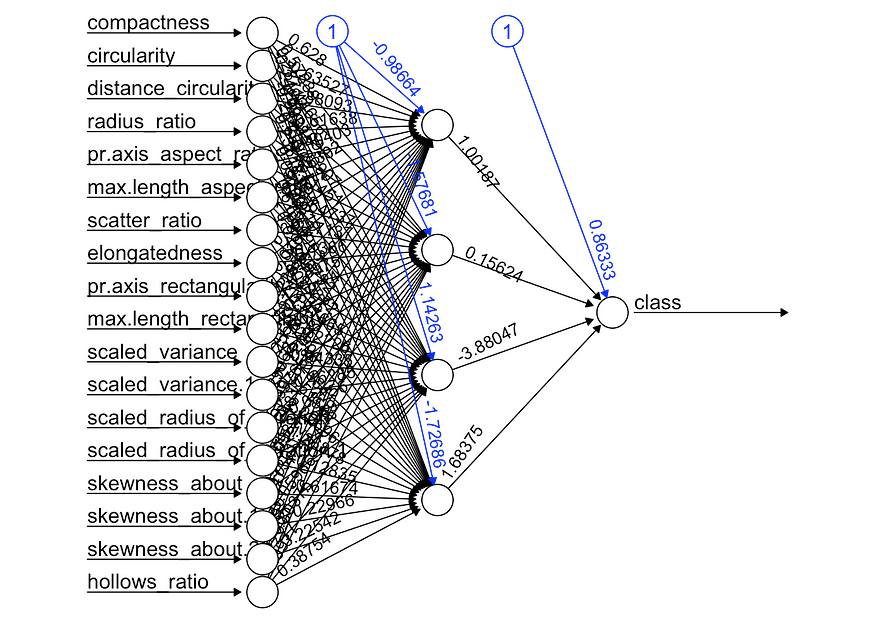

# Testing the result output
nn.results = compute( nn, testset )

results = data.frame( actual = test$class, prediction = round( nn.results$net.result ) )

# Confusion matrix
library( caret )
t = table( results )
print( confusionMatrix( t ) )
## Confusion Matrix and Statistics
## 
##       prediction
## actual  0  1
##      0 79  0
##      1 79 16
##                                                 
##                Accuracy : 0.545977              
##                  95% CI : (0.4688867, 0.6214742)
##     No Information Rate : 0.908046              
##     P-Value [Acc > NIR] : 1                     
##                                                 
##                   Kappa : 0.1553398             
##  Mcnemar's Test P-Value : <0.0000000000000002   
##                                                 
##             Sensitivity : 0.5000000             
##             Specificity : 1.0000000             
##          Pos Pred Value : 1.0000000             
##          Neg Pred Value : 0.1684211             
##              Prevalence : 0.9080460             
##          Detection Rate : 0.4540230             
##    Detection Prevalence : 0.4540230             
##       Balanced Accuracy : 0.7500000             
##                                                 
##        'Positive' Class : 0                     
##

三、步加入 PCA 的结果

        看来我们得到了一些结果。首先，看一下混淆矩阵。基本上，混淆矩阵表示有多少示例被分类到类中。主对角线显示正确分类的示例，次要对角线显示错误分类。在第一个结果中，分类器表现出非常混乱，因为它正确地分类了几乎所有来自“saab”类的示例，但它也将“bus”类的大多数示例分类为“saab”类。强化这个结果，我们可以看到准确率值在50%左右，对于分类任务来说，这是一个非常糟糕的结果。分类器基本上有 50% 的概率将新示例分类为“汽车”类，50% 的概率分类为“公共汽车”类。类似地，神经网络为每个新示例抛硬币，以选择它应该将其分类为哪个类。

四、让我们看看PCA是否可以帮助我们

        现在，让我们对数据集执行主成分分析，并获取特征值和特征向量。实际上，您将看到 R 包中的 PCA 函数提供了一组已按降序排序的特征值，这意味着第一个分量是方差最高的分量，第二个分量是方差第二高的特征向量，依此类推。下面的代码显示了如何选择特征向量查看特征值。

# PCA
pca_trainset = trainset %>% select( -class )
pca_testset = testset
pca = prcomp( pca_trainset, scale = T )

# variance
pr_var = ( pca$sdev )^2 

# % of variance
prop_varex = pr_var / sum( pr_var )

# Plot
plot( prop_varex, xlab = "Principal Component", 
                  ylab = "Proportion of Variance Explained", type = "b" )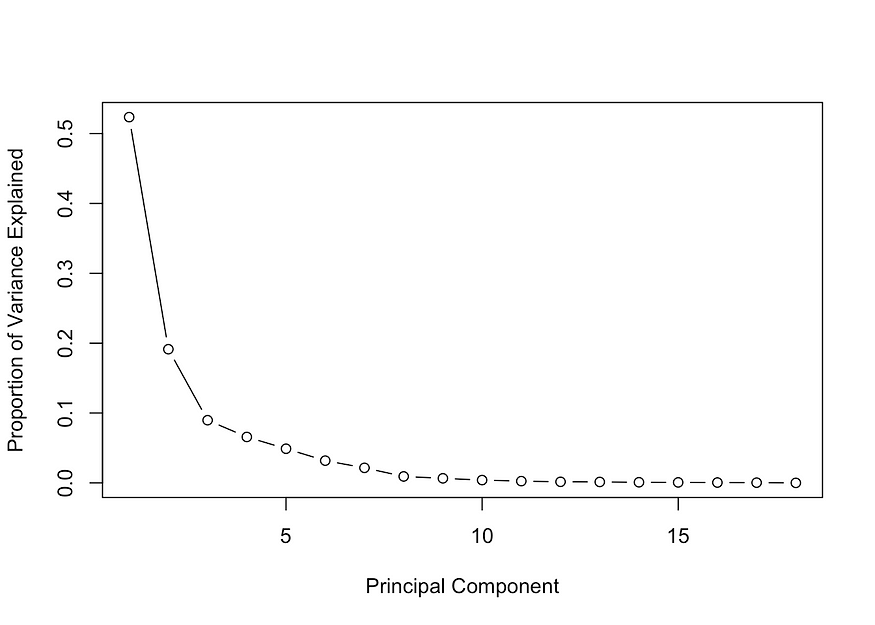

 # Scree Plot 
plot( cumsum( prop_varex ), xlab = "Principal Component", 
                            ylab = "Cumulative Proportion of Variance Explained", type = "b" )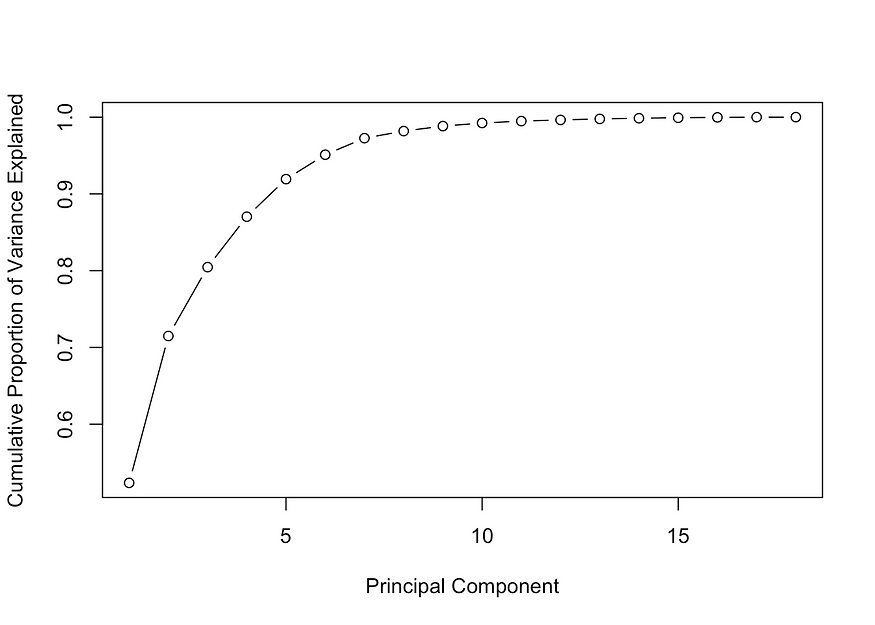 

        来自统计信息默认包的本机 R 函数“prcomp”执行 PCA，它返回所需的所有特征值和特征向量。第一个图显示每个特征的方差百分比。您可以看到第一个分量的方差最高，值约为 50%，而第 8 个分量约为方差的 0%。因此，它表明我们应该拿起前八个组件。第二个图显示了方差的另一个视角，尽管所有方差的累积总和，您可以看到前八个特征值对应于所有方差的大约 98%。事实上，这是一个相当不错的数字，这意味着只有2%的信息丢失。最大的好处是，我们正在从一个有十八个特征的空间转移到另一个只有八个特征的空间，只丢失2%的信息。这绝对是降维的力量。

        现在我们知道了将构成新空间的特征的数量，让我们创建新数据集，然后再次对神经网络进行建模，并检查我们是否获得了新的更好的结果。

# Creating a new dataset
train = data.frame( class = trainset$class, pca$x )
t = as.data.frame( predict( pca, newdata = pca_testset ) )

new_trainset = train[, 1:9]
new_testset =  t[, 1:8]

# Build the neural network (NN)
library( neuralnet )
n = names( new_trainset )
f = as.formula( paste( "class ~", paste( n[!n %in% "class" ], collapse = "+" ) ) )
nn = neuralnet( f, new_trainset, hidden = 4, linear.output = FALSE, threshold=0.01 )

# Plot the NN
plot( nn, rep = "best" )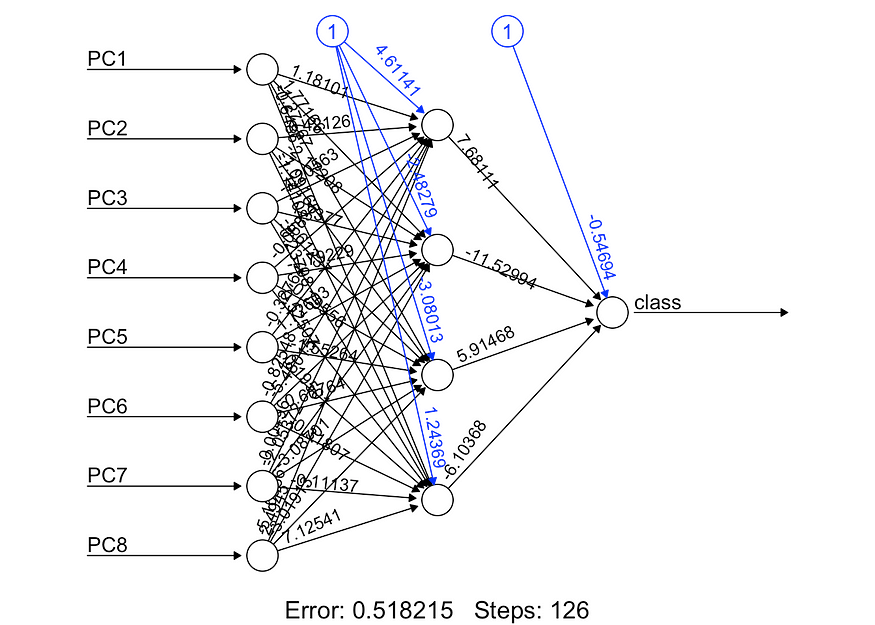

# Test the resulting output
nn.results = compute( nn, new_testset )

# Results
results = data.frame( actual = test$class, 
                      prediction = round( nn.results$net.result ) )

# Confusion Matrix
library( caret )
t = table( results ) 
print( confusionMatrix( t ) )
## Confusion Matrix and Statistics
## 
##       prediction
## actual  0  1
##      0 76  3
##      1  1 94
##                                                 
##                Accuracy : 0.9770115             
##                  95% CI : (0.9421888, 0.9937017)
##     No Information Rate : 0.5574713             
##     P-Value [Acc > NIR] : < 0.00000000000000022 
##                                                 
##                   Kappa : 0.9535318             
##  Mcnemar's Test P-Value : 0.6170751             
##                                                 
##             Sensitivity : 0.9870130             
##             Specificity : 0.9690722             
##          Pos Pred Value : 0.9620253             
##          Neg Pred Value : 0.9894737             
##              Prevalence : 0.4425287             
##          Detection Rate : 0.4367816             
##    Detection Prevalence : 0.4540230             
##       Balanced Accuracy : 0.9780426             
##                                                 
##        'Positive' Class : 0                     
##

        好吧，我想我们现在得到了更好的结果。让我们仔细检查一下。

        这次混淆矩阵显示出非常好的结果，神经网络在两个类中的错误分类较少，可以看出主对角线的值和准确率值在 95% 左右。这意味着分类器有 95% 的机会正确分类一个新的看不见的示例。对于分类问题，这根本不是一个不错的结果。

五、结论

        降维在机器学习中起着非常重要的作用，尤其是当您处理数千个特征时。主成分分析是顶级降维算法之一，在实际项目中不难理解和使用。正如我们在这篇文章中看到的那样，这种技术除了使特征操作的工作更容易之外，它仍然有助于改善分类器的结果。

        最后，初始问题的答案是肯定的，确实主成分分析有助于改善分类器的结果。

六、下一步是什么？

        正如我之前提到的，还有其他降维技术可用，例如线性判别分析、因子分析、等距图及其变体。ideia是探索每个人的优缺点，并单独和组合检查其结果。LDA与PCA相结合会改善分类器的结果吗？好吧，让我们在下一篇文章中调查一下。