112. 路径总和
文章目录
- [112. 路径总和](https://leetcode.cn/problems/path-sum/)
- 一、题目
- 二、题解
- 方法一:递归存储各个路径之和
- 方法二:递归版本2
- 简化版本
一、题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
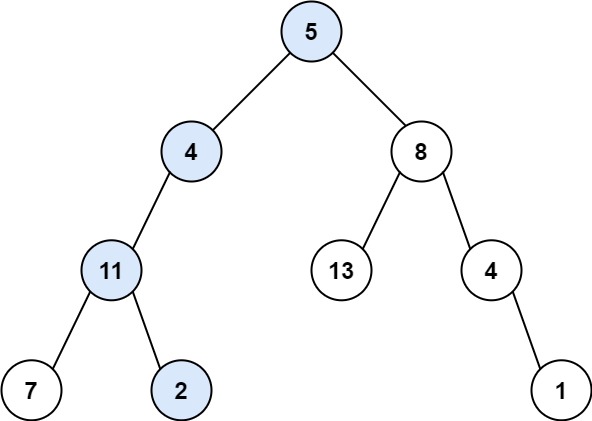
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
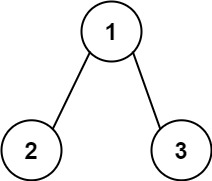
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
二、题解
方法一:递归存储各个路径之和
我们可以采取一种深度优先搜索的递归方法来解决。
算法思路
- 我们可以从根节点开始,递归地向下搜索每条路径,计算路径上节点值的和。
- 当遇到叶子节点时,即没有左子节点和右子节点的节点,将当前路径的和加入结果数组中。
- 最后,遍历结果数组,检查是否存在与目标和相等的路径和。
具体实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 辅助函数,递归计算路径和
void getSum(TreeNode* root, int sum, vector<int>& result){
if(root == nullptr) return;
int sum_r = sum + root->val;
// 当前节点为叶子节点时,将路径和加入结果数组
if(!root->left && !root->right){
result.push_back(sum_r);
}else{
getSum(root->left, sum_r, result);
getSum(root->right, sum_r, result);
}
}
// 主函数,判断是否存在路径和等于目标和
bool hasPathSum(TreeNode* root, int targetSum) {
vector<int> result;
getSum(root, 0, result);
// 遍历结果数组,检查是否存在与目标和相等的路径和
for(auto i: result){
if(i == targetSum){
return true;
}
}
return false;
}
};
算法分析
- 时间复杂度:遍历整棵树的时间复杂度为 O(n),其中 n 是树中节点的数量。这是因为我们需要访问每个节点一次以计算路径和。对结果数组进行遍历的时间复杂度是 O(n)。
- 空间复杂度:在递归过程中,我们需要存储每条路径的和,因此递归调用的最大深度不会超过树的高度,即 O(h),其中 h 是树的高度。在存储结果数组时,最坏情况下需要 O(n) 的空间。
方法二:递归版本2
这个版本不需要数组的存储
算法思路
- 我们定义一个递归函数
traversal,该函数接受三个参数:当前节点cur,当前路径的和count,和目标和target。 - 在
traversal函数中,首先判断当前节点是否为叶子节点,如果是叶子节点并且路径和等于目标和,则返回true,否则返回false。 - 如果当前节点不是叶子节点,则尝试向左子树和右子树递归,分别计算新的路径和,然后将两次递归的结果进行逻辑或运算,最终返回。
具体实现
class Solution {
public:
bool traversal(TreeNode *cur, int count, int target){
// 到达叶子节点时判断路径和是否等于目标和
if (count == target && !cur->left && !cur->right) {
return true;
}
// 到达叶子节点但路径和不等于目标和
if (!cur->left && !cur->right) {
return false;
}
bool left_b = false;
bool right_b = false;
// 递归搜索左子树
if (cur->left) {
left_b = traversal(cur->left, count + cur->left->val, target);
}
// 递归搜索右子树
if (cur->right) {
right_b = traversal(cur->right, count + cur->right->val, target);
}
// 返回左子树和右子树递归的结果的逻辑或
return (left_b || right_b);
}
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return false;
}
return traversal(root, root->val, targetSum);
}
};
算法分析
- 时间复杂度:遍历整棵树的时间复杂度为 O(n),其中 n 是树中节点的数量。每个节点最多被访问一次。
- 空间复杂度:递归调用的最大深度不会超过树的高度,即 O(h),其中 h 是树的高度。在递归过程中,只使用了常数级别的额外空间。
简化版本
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return false;
}
if (!root->left && !root->right) {
return root->val == targetSum;
}
int remainingSum = targetSum - root->val;
return hasPathSum(root->left, remainingSum) || hasPathSum(root->right, remainingSum);
}
};