1、全排列

全排列（Permutation）：全排列是指给定一组元素，通过交换元素的位置，得到这组元素所有可能的排列方式。假设有n个元素，全排列将产生n!（n的阶乘）种不同的排列方式。
eg：对于集合{1, 2, 3}的全排列有6个，分别为：
{1, 2, 3}
{1, 3, 2}
{2, 1, 3}
{2, 3, 1}
{3, 1, 2}
{3, 2, 1}

算法思路：

①回溯（DFS）交换法

一个序列的全排列，可以理解为其中每几个数发生了交换形成。对于一个长度为n的序列，我们可以取[0, flag - 1]为已经确定下来的数，flag将要与[flag + 1, n - 1]中每个数发生交换，交换一次就会形成一个新的排列。（因此每次递归完成后，要将上一次交换后的两个数字交换回来）
每次交换完成后，flag位置发生变化，会形成新的[0, flag - 1]，flag又将要与新的[flag + 1, n - 1]中每个数发生交换。在此进行回溯，示例图如下：来源于leetcode46

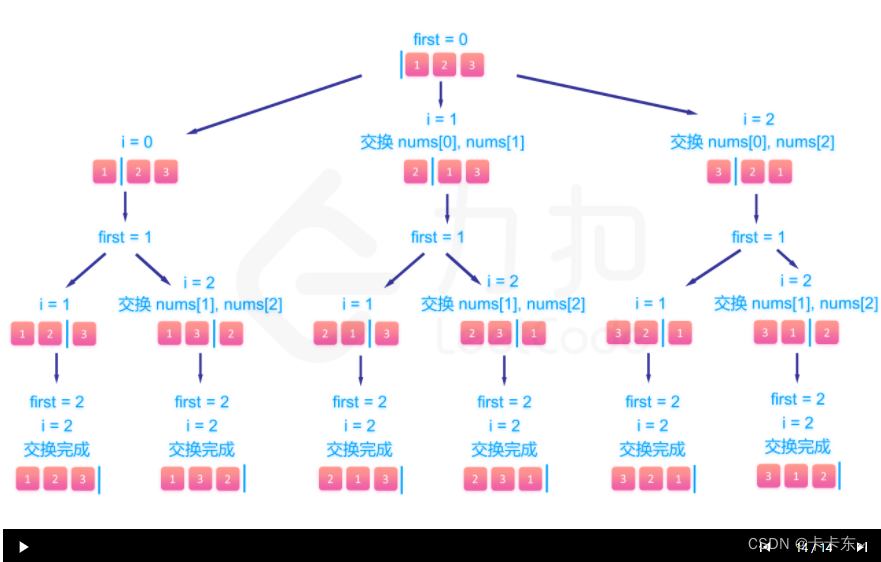
代码如下: 这也是一个经典的DFS模板

public static List<List<Integer>> permute(int[] nums) {
        //结果
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> integers = new ArrayList<>(nums.length);
        //方便操作
        for (int num : nums) {
            integers.add(num);
        }
        //主要方法
        backtrack(integers, result, 0);
        return result;
    }
    //递归回溯
    public static void backtrack(List<Integer> nums, List<List<Integer>> result, int flag) {
        //flag到头，说明后面没有可交换的数了，结果集add
        if (flag == nums.size() - 1) {
            result.add(new ArrayList<>(nums));
        }
        for (int i = flag; i < nums.size(); i++) {
            //[0, flag-1]为左区间，[flag, nums.size-1]为右区间
            //交换flag与i
            Collections.swap(nums, flag, i);
            //flag右移，进入递归
            backtrack(nums, result, flag + 1);
            //递归完成，回溯时要把上一步位置交换回来
            Collections.swap(nums, flag, i);
        }
    }

②回溯（DFS）选择法

主要是选与不选，但是选择了1，就不能再次选了，只能选2或者3。相比上边的交换法很容易理解。

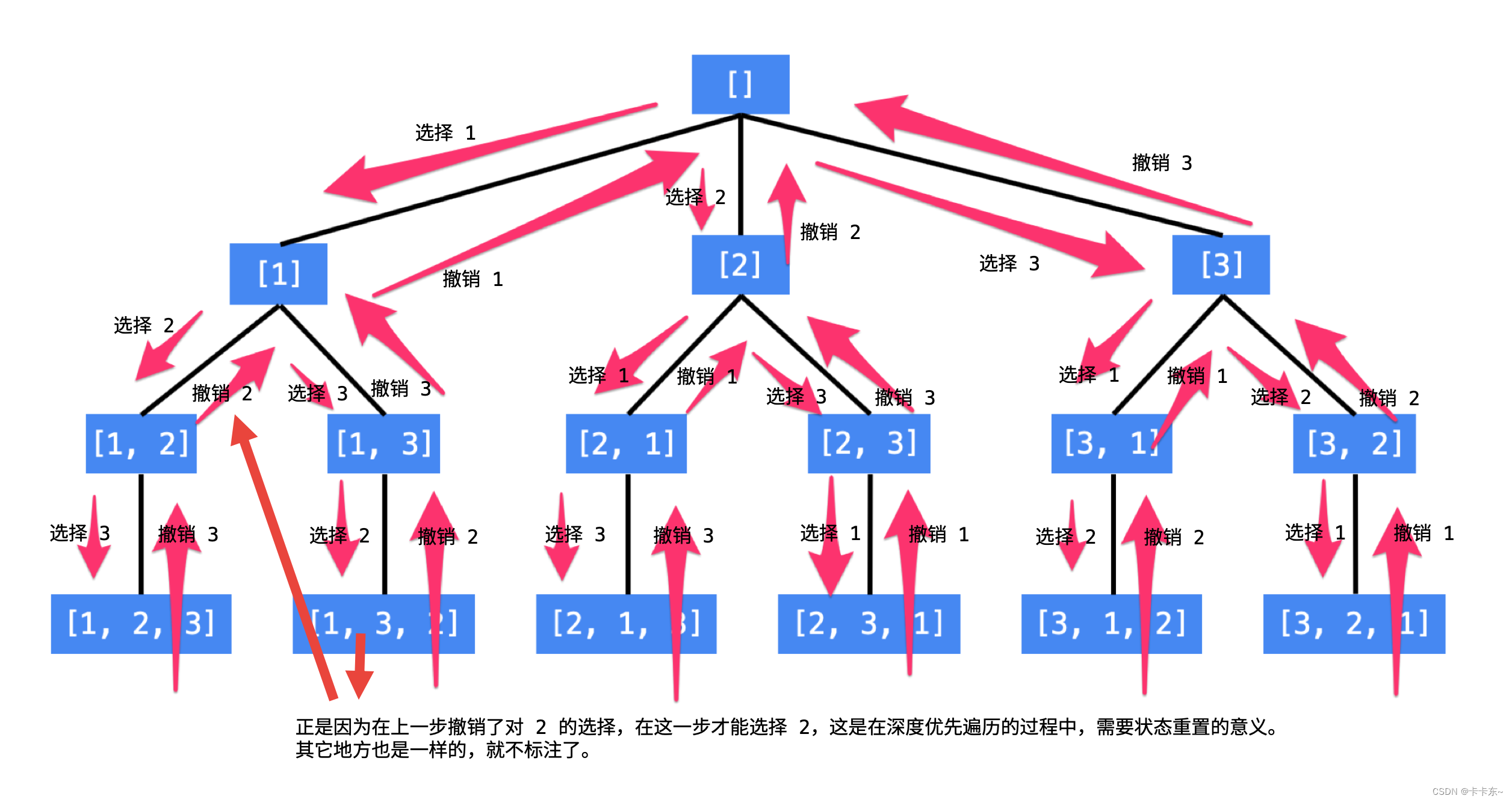
代码如下：

    List<List<Integer>> result = new ArrayList<>();
    //回溯选择法
    public void backtrack2(List<Integer> list, int[] nums){
        //最后一层也选完了
        if (list.size() == nums.length) {
            result.add(new ArrayList<>(list));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            //选择第i个,选完以后不能选了
            if (!list.contains(nums[i])){
                list.add(nums[i]);
                //进入下一层
                backtrack2(list, nums);
                //回溯后要留位置,把最后一个移除，让nums[i+1]进来，但是如果i已经循环完了，会再次回溯发生remove
                list.remove(list.size() - 1);
            }
        }
    }

最后的结果就是result。看一下这个代码：
1、参数分别为（list:每次选择的数，如果最后这个list的长度等于了原始数组长度，说明一次排列完成了。nums:原始数组）
2、循环nums，选择一个数放入list中，之后进入递归，再次循环nums[]，但是取过的数是不能取了，i++，取另一个数。直到list长度等于了原始数组长度。一次递归完成。
3、回溯，把递归前add进来的nums[i]移除，空出一个位置来，供其他数选择。此时，如果i也到头了，会再次发生回溯，再空出一个位置。也就是list中的数字会同时受到i的影响和回溯的影响。

举个例子：[1]，[1,2]，[1,2,3]，递归完成，发生回溯，remove了[3]，成为了[1，2]，（正常来想，再进入递归，又会是[1,2,3]了，这不是死循环了吗）。但是成为了[1,2]后，因为i++发生过一次，i=2了，此时在进入递归，i++使得i成为了3，又发生return，回溯，成为了[1]，这时候，因为i已经发生一次++，取过2了，因此只能取3。成为了[1,3]，然后取2,结果是[1,3,2]。

但是这个代码时间复杂度达到了nⁿ，因为每次都要循环n次，而且list.contains()也是一个n的复杂度。所以复杂度已经达到了(n*n)ⁿ。。。。。
第一种方式是n!的递归调用，因为i每次增加，循环就会减少。
优化方式：可以选一个额外的boolean数组保存状态原数组的index状态，如果被引用过，就置为true，循环时候进行判断即可，不需要contions。

③ 插入法

这个方法思想是：在[1]的基础上把2插进去有几个地方可以插，插完后得到一组数列比如[1,2]，然后再把3一个一个插进去，得到每个结果就是一个排列。代码没有写，和第一种交换思想差不多，这个可能需要一些额外空间

2、子集

子集是指给定一组元素，从中选取0个或多个元素组成的集合。对于n个元素的集合，它将包含2^n个不同的子集，包括空集和全集。

一般题目会是这样：

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

• 输入：nums = [1,2,3]
• 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

①回溯选择法

算法思想：有点类似上面全排列的选择法，就是遍历原始数组，取或者不取当前位置，取了当前位置，那么下一个位置也会面临取或者不取。回溯时，需要复位。有点类似二叉树的遍历。
代码如下：

    //表示结果
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();
	
	//求子集
    public List<List<Integer>> subsets1(int[] nums) {
        backTrack(0, nums);
        return res;
    }

    //递归回溯
    public void backTrack(int cur, int[] nums) {
        if (cur == nums.length) {
            //cur到头
            res.add(new ArrayList<>(temp));
            return;
        }
        //取当前位置的
        temp.add(nums[cur]);
        //进入递归，下一个位置
        backTrack(cur + 1, nums);
        //回溯，需归位，不能写temp.remove(cur);，应该移动的是最后进入temp的，和cur没关系，cur只和nums的下标有关系
        temp.remove(temp.size() - 1);
        //不取当前位置的，那么直接进入下一个位置
        backTrack(cur + 1, nums);
    }

② 动态规划

子集可以是从空集开始[]，遍历原始数组，空集基础上增加一个元素，成为[[ ], [1]]，再在此基础上加第二个元素成为[[ ]， [1]，[2]， [1，2]]，再在此基础上增加下一个元素。后一个状态依赖于前一个状态。反过来想，就可以得到状态转移方程：i表示当前状态，i-1表示上一个状态

 List<List>[i] = List<List>[i - 1]中的每一个list.add(nums[i])

虽然是一个数组嵌套，但是是一个一维的动态规划，只有i这一种依赖。
代码如下：

public List<List<Integer>> subsets2(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        result.add(new ArrayList<>());
        //取第i个数
        for (int i = 0; i < nums.length; i++) {
            List<List<Integer>> temp = new ArrayList<>();
            //遍历List<List>[i - 1]，获取每一个list
            for (List<Integer> list : result) {
                //每一个list.add(nums[i])
                List<Integer> news = new ArrayList<>(list);
                news.add(nums[i]);
                //中间变量保存
                temp.add(news);
            }
            //得到List<List>[i]
            result.addAll(temp);
        }
        return result;
    }

看着是两个for，但其实第二层for是动态变化的，而且每次扩容2倍，因此时间复杂度还是2ⁿ，相对于递归少了压栈空间

③ 位运算方式

有一种位运算的方式来模拟子集的形成，因为集合中的每个元素可以用一个二进制位来表示，1表示选择该元素，0表示不选择。通过遍历所有的二进制数，即可得到所有子集。但是我感觉遇到这个题是想不出这种方法来，所以没有写对应代码QAQ
位运算方式

组合

组合是指从一组元素中选取特定数量的元素，而不考虑它们的顺序。假设有n个元素，从中选择k个元素作为组合，可以用“C(n,k)”或者“n choose k”来表示，计算公式为$$C(n,k)=\frac{n!}{k!\cdot (n-k)!}$$
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

算法思想：