数字图像处理 - 图像采样和量化

news2024/11/16 1:21:51

1、目标

获取图像的方法有很多种，但最终的目标是一致的：从传感数据生成数字图像。大多数传感器的输出是连续的电压波形，其幅度和空间行为与被感测的物理现象有关。要创建数字图像，我们需要将连续感测数据转换为数字格式。这就需要两个过程：采样和量化。

2、基本概念

下图显示了想要转换为数字形式的连续图像f。图像在 x 和 y 坐标以及幅度上是连续的。为了将其数字化，我们必须在坐标和幅度中对函数进行采样。将坐标值数字化称为采样。将幅度值数字化称为量化。

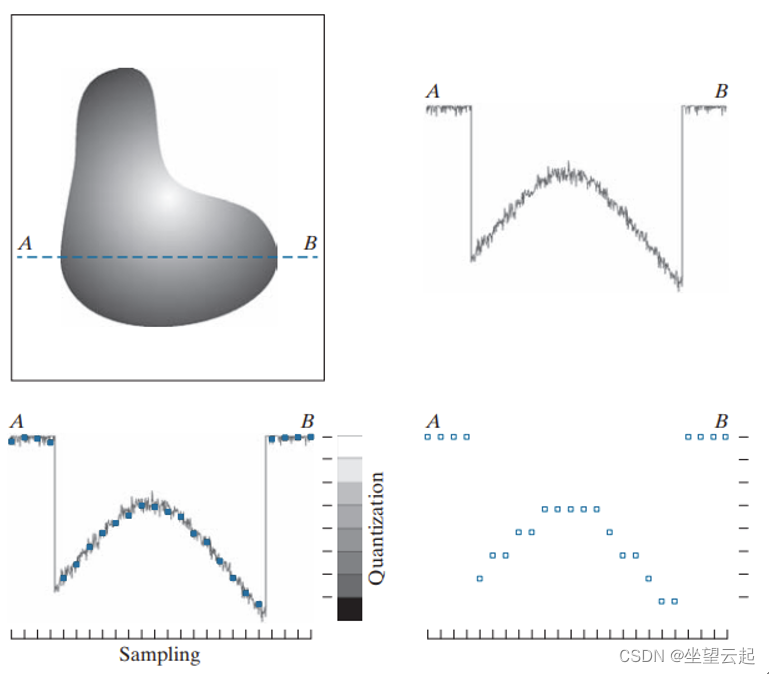
图 (a) 连续图像。 (b) 显示连续图像中沿线 AB 的强度变化的扫描线。(c) 采样和量化。(d) 数字扫描线。

图(b)中的一维函数是沿图(a)中线段AB的连续图像的幅度（强度级别）值的图。随机变化是由于图像噪声。为了对该函数进行采样，我们沿线AB取等间距的样本，如图(c)所示。样本显示为叠加在函数上的黑色小方块，它们的（离散）空间位置由图底部的相应刻度线表示。这组黑色方块构成了采样函数。然而，样本的值仍然跨越（垂直）强度值的连续范围。为了形成数字函数，还必须将强度值转换（量化）为离散量。图(c)中的垂直灰色条描绘了分为八个离散间隔的强度标度，范围从黑色到白色。垂直刻度线表示分配给八个强度间隔中的每一个的特定值。通过将八个值之一分配给每个样本来量化连续强度级别，具体取决于样本与垂直刻度线的垂直接近度。采样和量化产生的数字样本在图(d)中显示为白色方块。从连续图像的顶部开始，逐行向下执行此过程，生成二维数字图像。在图中暗示，除了使用的离散级别的数量外，在量化高度依赖于采样信号的噪声含量。

3、在实践中

在实践中，采样方法由用于生成图像的传感器布置确定。当图像由单个传感元件结合机械运动生成时，传感器的输出以上述方式量化。然而，空间采样是通过选择我们激活传感器收集数据的单个机械增量的数量来完成的。机械运动可以非常精确，因此原则上，我们可以使用这种方法对图像进行采样的精细程度几乎没有限制。实际上，采样精度的限制是由其他因素决定的，例如系统中使用的光学元件的质量。

当传感条用于图像采集时，条中传感器的数量在一个方向上确定结果图像中的样本，而机械运动在另一个方向上确定样本的数量。传感器输出的量化完成了生成数字图像的过程。

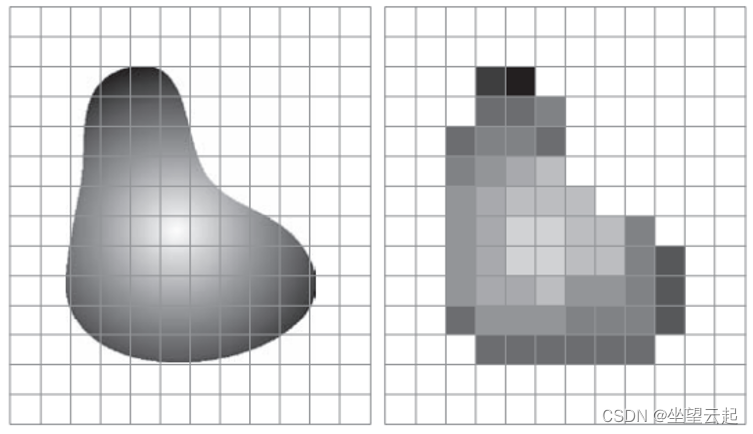
当传感阵列用于图像采集时，不需要运动。阵列中传感器的数量确定了双向采样的限制。传感器输出的量化如上所述。上图说明了这个概念。图(a) 显示了投影到二维传感器平面上的连续图像。图(b) 显示了采样和量化后的图像。数字图像的质量在很大程度上取决于采样和量化中使用的样本数量和离散强度级别。但是，图像内容在这些参数的选择中也起着重要作用。

4、图像插值

插值用于缩放、缩小、旋转和几何校正数字图像等任务。我们在本节中的主要目标是介绍插值并将其应用于图像大小调整（缩小和缩放），这基本上是图像重采样方法。

插值是使用已知数据估计未知位置的值的过程。假设大小为500*500像素的图像必须放大 1.5 倍至 750*750像素。可视化缩放的一种简单方法是创建一个与原始图像具有相同像素间距的假想 750*750网格，然后将其缩小以使其与原始图像完全重叠。显然，缩小后的 750*750网格中的像素间距会小于原始图像中的像素间距。要将强度值分配给叠加层中的任何点，我们会在底层原始图像中查找其最近的像素，并将该像素的强度分配给 750*750网格中的新像素。当强度已分配给覆盖网格中的所有点时，我们将其扩展回指定大小以获得调整大小的图像。

上一段讨论的方法称为最近邻插值，因为它为每个新位置分配原始图像中其最近邻的强度。这种方法很简单，但它有产生不良伪影的趋势，例如直尺的严重变形。更合适的方法是双线性插值，其中我们使用四个最近邻来估计给定位置的强度。令(x,y)表示我们要为其分配强度值的位置的坐标（将其视为前面描述的网格的一个点），并让 v(x,y) 表示该强度值。对于双线性插值，使用等式获得分配的值。