文章目录
- 网格简化(QEM)
- 1 概述与原理
- 1.1 网格简化的应用
- 1.2 常见的简化操作
- 1.3 二次误差度量
- 2 算法流程
- 2.1 逐步分析
- 3 Python代码实现
- 3.1 测试结果
- 4 总结
- 参考
网格简化(QEM)
1 概述与原理
网格简化,通过减少复杂网格数据的顶点、边和面的数量简化模型的表达,在图形学领域,这种技术也叫做Level of details(LOD,多层次细节)。
1.1 网格简化的应用
- 多分辨率渲染:对于投影尺寸较小(远距离显示)的模型,可以渲染它的简化版本替代原本丰富细节的高复杂度网格,提高渲染效率。
- 代理仿真:在简化模型上进行仿真,然后通过插值方法得到原本复杂网格的近似仿真结果,提高仿真效率。 [ 1 ] ^{[1]} [1]
1.2 常见的简化操作
-
Vertex Decimation(顶点抽取)
选择一个顶点进行删除,移除该顶点相邻的面,然后对产生的孔洞重新三角化。
-
Vertex Clustering(顶点聚类)
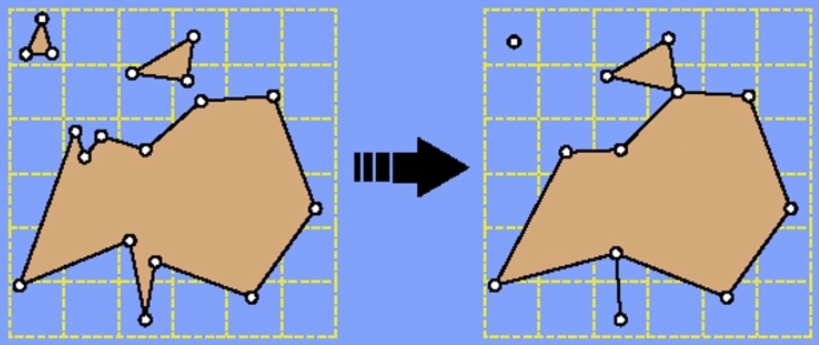
划分原始网格的包围盒成一个grid,将每个cell中的顶点聚类成一个,然后依据聚类后得到的顶点更新网格的面。
-
Edge Contraction(边收缩)
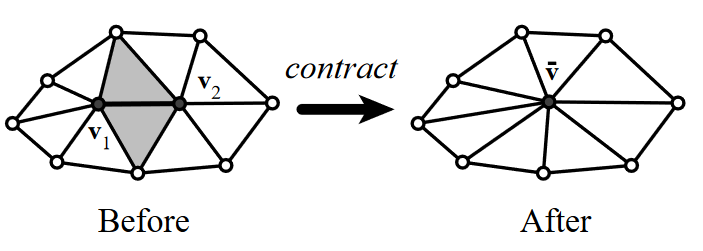
( v 1 , v 2 ) → v ‾ (v_1,v_2)\rightarrow{\overline{v}} (v1,v2)→v,将一条边收缩为一个点,删除退化的面(上图中阴影所示)。
-
Pair Contraction(点对收缩)
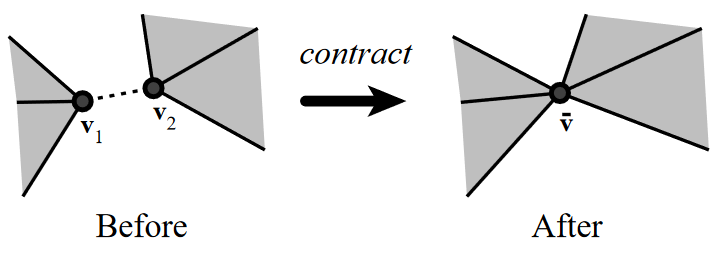 作为边收缩的推广,如果点对
(
v
1
,
v
2
)
(v_1,v_2)
(v1,v2)是一条边,那么等同于边收缩;如果点对
(
v
1
,
v
2
)
(v_1,v_2)
(v1,v2)不是一条边,那么对该点对进行收缩会使原本不相连的部分连接到一起。
作为边收缩的推广,如果点对
(
v
1
,
v
2
)
(v_1,v_2)
(v1,v2)是一条边,那么等同于边收缩;如果点对
(
v
1
,
v
2
)
(v_1,v_2)
(v1,v2)不是一条边,那么对该点对进行收缩会使原本不相连的部分连接到一起。
1.3 二次误差度量
为了保证收缩后的顶点与原始网格之间的局部距离不要太远,我们选择一种基于二次距离度量的方式寻找最优的收缩点。
根据二次距离寻找最优收缩点

此处公式推导请移步至网格简化 QEM 方法详解,文中讲得十分清晰。
考虑一次边收缩。对于两个点 v 1 , v 2 v_1, v_2 v1,v2 ,收缩成一个点 v ˉ \bar{v} vˉ 。定义 plane ( v i ) \left(v_i\right) (vi) 表示 v i v_i vi 对应的那些原始三角面,则我们的优化目标是
v ˉ = arg min v ∑ p ∈ plane ( v 1 ) ∪ plane ( v 2 ) distance ( v , p ) 2 \bar{v}=\underset{v}{\arg \min } \sum_{p \in \text { plane }\left(v_1\right) \cup \text { plane }\left(v_2\right)} \operatorname{distance}(v, p)^2 vˉ=vargminp∈ plane (v1)∪ plane (v2)∑distance(v,p)2
下面一步步化简。令平面 p p p 的表达式为 a x + b y + c z + d = 0 a x+b y+c z+d=0 ax+by+cz+d=0 ,其中 a 2 + b 2 + c 2 = 1 a^2+b^2+c^2=1 a2+b2+c2=1 。 记 v = [ x , y , z , 1 ] T , p = [ a , b , c , d ] T v=[x, y, z, 1]^T, p=[a, b, c, d]^T v=[x,y,z,1]T,p=[a,b,c,d]T ,可得
distance ( v , p ) 2 = ( v T p ) 2 = v T p p T v = v T K p v \operatorname{distance}(v, p)^2=\left(v^T p\right)^2=v^T p p^T v=v^T K_p v distance(v,p)2=(vTp)2=vTppTv=vTKpv
其中 K p = p p T K_p=p p^T Kp=ppT ,则原式简化为
v ˉ = arg min v v T ( ∑ p ∈ plane ( v 1 ) ∪ p l a n e ( v 2 ) K p ) v \bar{v}=\underset{v}{\arg \min }\space v^T\left(\sum_{p \in \text { plane }\left(v_1\right) \cup p l a n e\left(v_2\right)} K_p\right) v vˉ=vargmin vT p∈ plane (v1)∪plane(v2)∑Kp v
此处取约等于
v ˉ ≈ arg min v v T ( ∑ p ∈ plane ( v 1 ) K p + ∑ p ∈ plane ( v 2 ) K p ) v \bar{v} \approx \underset{v}{\arg \min }\space v^T\left(\sum_{p \in \operatorname{plane}\left(v_1\right)} K_p+\sum_{p \in \operatorname{plane}\left(v_2\right)} K_p\right) v vˉ≈vargmin vT p∈plane(v1)∑Kp+p∈plane(v2)∑Kp v
令 Q i = ∑ p ∈ plane ( v i ) K p Q_i=\sum_{p \in \text { plane }\left(v_i\right)} K_p Qi=∑p∈ plane (vi)Kp ,则有
v ˉ = arg min v v T ( Q 1 + Q 2 ) v \bar{v}=\underset{v}{\arg \min }\space v^T\left(Q_1+Q_2\right) v vˉ=vargmin vT(Q1+Q2)v
初始化时,将 plane ( v ) \operatorname{plane}(v) plane(v) 设为点 v \mathrm{v} v 周围的三角形面即可。此时上面的约等号并无大碍,因为一个 三角形面至多重复三次 (三个顶点),不仅不会带来较大的误差,而且简化了计算。
另外, K p K_p Kp 是对称矩阵,故 Q Q Q 也是,所以只需要存储 10 个元素即可。
此时求解 v ˉ \bar{v} vˉ 的坐标变成求解二次函数极值点。 [ 2 ] ^{[2]} [2]
令
Q
=
Q
1
+
Q
2
Q=Q_1+Q_2
Q=Q1+Q2,通过解如下方程求解
v
ˉ
\bar{v}
vˉ的坐标:
[
q
11
q
12
q
13
q
14
q
12
q
22
q
23
q
24
q
13
q
23
q
33
q
34
0
0
0
1
]
v
ˉ
=
[
0
0
0
1
]
\left[{\begin{array}{cccc}q_{11}&q_{12}&q_{13}&q_{14}\\q_{12}&q_{22}&q_{23}&q_{24}\\q_{13}&q_{23}&q_{33}&q_{34}\\0&0&0&1\end{array}}\right]\bar{v}=\left[{\begin{array}{c}0\\0\\0\\1\end{array}}\right]
q11q12q130q12q22q230q13q23q330q14q24q341
vˉ=
0001
上式中,
q
11
q_{11}
q11表示
Q
Q
Q的第一行的第一个元素的值,这里
v
ˉ
\bar{v}
vˉ使用的是齐次坐标。如果上式中左侧矩阵可逆,则
v
ˉ
=
[
q
11
q
12
q
13
q
14
q
12
q
22
q
23
q
24
q
13
q
23
q
33
q
34
0
0
0
1
]
−
1
[
0
0
0
1
]
\bar{v}=\left[{\begin{array}{cccc}q_{11}&q_{12}&q_{13}&q_{14}\\q_{12}&q_{22}&q_{23}&q_{24}\\q_{13}&q_{23}&q_{33}&q_{34}\\0&0&0&1\end{array}}\right]^{-1}\left[{\begin{array}{c}0\\0\\0\\1\end{array}}\right]
vˉ=
q11q12q130q12q22q230q13q23q330q14q24q341
−1
0001
如果不可逆,则
[
4
]
^{[4]}
[4]
v
=
(
1
−
k
)
v
1
+
k
v
2
,
where
k
∈
[
0
,
1
]
v
ˉ
=
arg
min
v
v
T
(
Q
1
+
Q
2
)
v
v=(1-k)v_1+kv_2,\text{where}\space{k}\in[0,1]\\ \bar{v}=\underset{v}{\arg \min }\space v^T\left(Q_1+Q_2\right) v
v=(1−k)v1+kv2,where k∈[0,1]vˉ=vargmin vT(Q1+Q2)v
如果还是不行,就选择端点
v
1
,
v
2
v_1,v_2
v1,v2或者中点
v
1
+
v
2
2
\frac{v_1+v_2}2
2v1+v2三者中误差(
Δ
(
v
)
=
v
T
Q
v
\Delta(v)=v^TQv
Δ(v)=vTQv)最小的作为
v
ˉ
\bar{v}
vˉ
[
3
]
^{[3]}
[3]。
2 算法流程

图源自:QEM网格简化 - 简书 (jianshu.com)
2.1 逐步分析
-
计算所有初始顶点的 Q Q Q矩阵
令平面 p p p 的表达式为 a x + b y + c z + d = 0 a x+b y+c z+d=0 ax+by+cz+d=0 ,其中 a 2 + b 2 + c 2 = 1 a^2+b^2+c^2=1 a2+b2+c2=1 。记 p = [ a , b , c , d ] T p=[a, b, c, d]^T p=[a,b,c,d]T。由此,我们定义 Q i Q_i Qi(4x4,顶点 v i v_i vi的 Q Q Q矩阵)如下:
Q i = ∑ p ∈ p l a n e s ( v i ) p p T Q_i=\sum_{p\in planes(v_i)}pp^T Qi=p∈planes(vi)∑ppT -
选择合法点对
一个顶点对 ( v i , v j ) (v_i,v_j) (vi,vj)是合法点对的条件为:
- ( v i , v j ) (v_i,v_j) (vi,vj)是一条边;
- ‖ v i − v j ‖ < t ‖v_i − v_j‖ < t ‖vi−vj‖<t, t t t为阈值参数。
以上条件满足其一即可。
-
计算每个合法点对 ( v i , v j ) (v_i,v_j) (vi,vj)的最小收缩误差 c o s t i j cost_{ij} costij,以及最佳收缩点 v o p t v_{opt} vopt的位置
首先计算 v o p t v_{opt} vopt对应的 Q o p t Q_{opt} Qopt:
Q o p t = Q i + Q j = [ q 11 q 12 q 13 q 14 q 12 q 22 q 23 q 24 q 13 q 32 q 33 q 34 q 14 q 24 q 34 q 44 ] . Q_{opt}=Q_i+Q_j=\begin{bmatrix}q_{11}&q_{12}&q_{13}&q_{14}\\q_{12}&q_{22}&q_{23}&q_{24}\\q_{13}&q_{32}&q_{33}&q_{34}\\q_{14}&q_{24}&q_{34}&q_{44}\end{bmatrix}. Qopt=Qi+Qj= q11q12q13q14q12q22q32q24q13q23q33q34q14q24q34q44 .
定义 c o s t i j cost_{ij} costij如下:
c o s t i j = v T Q o p t v cost_{ij}=v^TQ_{opt}v costij=vTQoptv
最小化收缩误差,得到 v o p t v_{opt} vopt。具体计算参见上一节[二次误差度量](#1.3 二次误差度量)。 -
将所有合法点对按其对应的 c o s t i j cost_{ij} costij的顺序放置在一个堆中,最小 c o s t i j cost_{ij} costij对位于顶部
一般使用小根堆进行排序。
-
移除最小 c o s t i j cost_{ij} costij对应的点对,收缩 ( v i , v j ) → v o p t (v_i,v_j)\rightarrow{v_{opt}} (vi,vj)→vopt,更新所有包含了 v i v_i vi或 v j v_j vj的合法点对的 c o s t cost cost
这一步是迭代进行的,结束的标志为达到了设定的简化率或者堆空了 [ 5 ] ^{[5]} [5]。
3 Python代码实现
代码实现方面,推荐直接学习该项目:Mesh_simplification_python: An implementation of mesh simplification algorithm using python,其中代码注释很全,条理清晰,值得学习。
3.1 测试结果
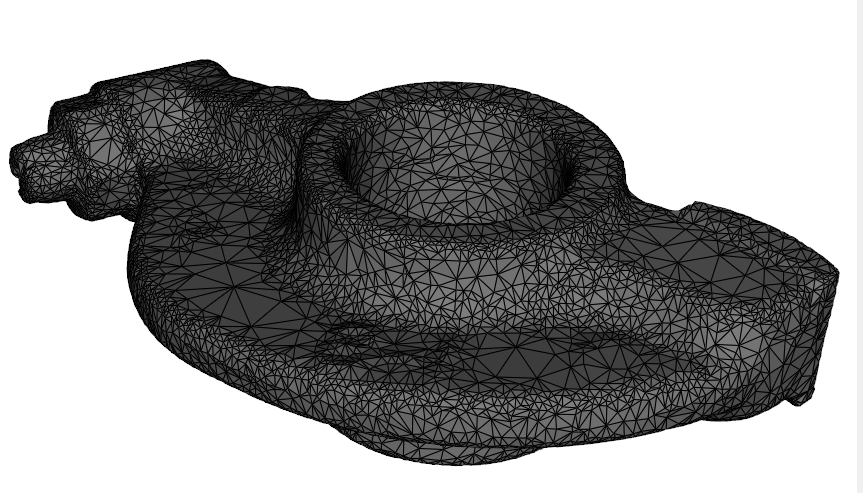
输入模型网格(9397 vertices, 18794 faces):
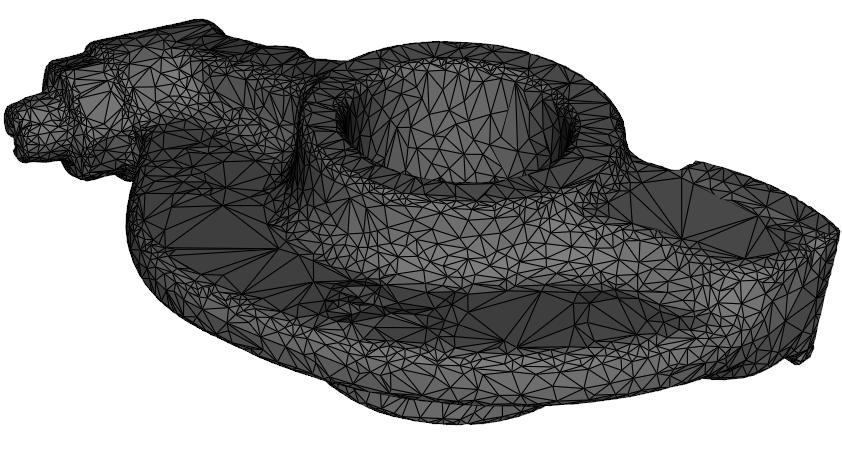
t = 0 , r a t i o = 0.5 t=0,\space ratio=0.5 t=0, ratio=0.5(4698 vertices, 9396 faces):
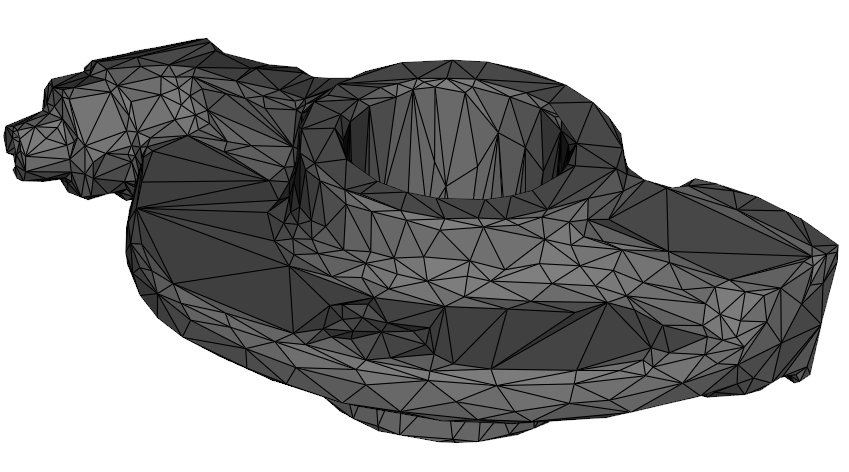
t = 0 , r a t i o = 0.1 t=0,\space ratio=0.1 t=0, ratio=0.1(939 vertices, 1878 faces):
4 总结
-
代码功能优化
在原论文中还提到了如下两个细节:
-
保留边界
对于一些在简化过程中需要保持边界的模型网格,我们在点对收缩时判断点对是否为边界边,如果是,我们可以给该点对cost加权一个较大的惩罚因子,阻止收缩。
-
防止面片翻转
直接使用QEM算法进行网格简化,可能会导致一些面片翻转。所以我们需要在计算点对收缩cost时,同时判断点对的每一个相邻面片是否发生了翻转。可采用收缩前后面片法向量的夹角大小进行判断。同时,我们也对其代价进行惩罚。
-
参考
[1] GAMES102:几何建模与处理
[2] https://zhuanlan.zhihu.com/p/411865616
[3] Michael Garland and Paul S. Heckbert. 1997. Surface simplification using quadric error metrics. In Proceedings of the 24th annual conference on Computer graphics and interactive techniques (SIGGRAPH '97). ACM Press/Addison-Wesley Publishing Co., USA, 209–216. https://doi.org/10.1145/258734.258849
[4] https://www.jianshu.com/p/2bf615c38165
[5] https://github.com/AntonotnaWang/Mesh_simplification_python