在文章末尾的公众号回复：深圳杯B题，获取完整内容。
本文的文本、公式、代码都是部分展示。

一、题目

B题 电子资源版权保护问题

版权又称著作权，包括发表权、署名权、修改权、保护作品完整权、复制权、发行权、出租权、展览权、表演权、放映权、广播权、信息网络传播权、摄制权、改编权、翻译权、汇编权及应当由著作权人享有的其他权利。

在计算机网络广泛应用的今天，越来越多电子资源会通过网络进行快速传递。与此同时，如何保护电子资源的著作权问题也渐渐变得至关重要。这一问题也是信息安全领域中的关键问题之一。数字水印（electronic water mark）技术是解决这一问题的关键技术之一。但因为可见水印（visible watermarking）在应用于电子图片著作权保护时，往往会破坏图片自身的结构，并且因嵌入信息可见而容易被识别剔除。因此，隐写术（steganography）被广为关注和使用。

隐写术一般被认为是信息隐藏学的一个重要分支，它专门研究如何隐藏实际存在的信息。隐写术有悠久的历史，部分案例甚至可追溯到公元前数百年。随着计算机和互联网技术的高速发展，近代隐写技术的研究被认为大约起始于20世纪90年代。因为隐写技术能将特定信息嵌入信息载体且不易被察觉，所以它可被广泛地应用于著作权保护、数据附加等领域。

• 问题1 针对附件1的图片P，建立生成嵌入信息“深圳杯数学建模挑战赛”的图片SP的数学模型，使得图片SP在人的视觉上尽可能与原图P相近。设计并实现生成图片SP的算法，将生成SP源代码和结果图片SP置于参赛作品的附录A中；给出从图片SP提取著作权信息使用的源代码并置于参赛作品的附录B中。
• 问题2 使用问题1中的模型与算法，能否将《中华人民共和国著作权法》（第三次修正案）[1]中的所有文字信息嵌入附件1的图片中？如果不能，最多能嵌入多少？
• 问题3 在电子图片传递的过程中，可能会被压缩或以不同的图片格式存储，也可能会被缩放、旋转或其他几何变形等。此时，问题1中的算法是否仍然可用？如果不能用，如何改进？
• 问题4 若要保护其他电子图片的著作权，使用问题1中的算法时应注意什么？请给出最多3条注意事项，并说明理由。

参考文献

---

[1] http://www.gov.cn/guoqing/2021-10/29/content_5647633.htm

二、思路 与 解答

2.1 问题一

2.11 LSB 方法测试

可以使用lsb方法来实现。

LSB隐写就是利用图像的最低有效位（Least Significant Bit，LSB）来隐藏信息的技术。图像的每个像素由三种颜色（红绿蓝）组成，每种颜色占8位，也就是一个字节。LSB隐写就是把要隐藏的信息的二进制位替换掉图像每个像素的最低位，从而实现信息的嵌入。由于最低位对图像的质量影响很小，人眼很难察觉出差异，所以这种方法具有较好的隐蔽性 。

可以调用stegano库来进行测试，看看lsb方法效果如何：

• 该库要求输入图片为PNG格式，所以先将原图转换为PNG格式。
• 该库对中文支持不好（即时使用UTF-8），所以本文先将要嵌入的信息进行base64编码再嵌入到图片中；
• 解析图片中的信息时，则逆过来操作。

...

# 嵌入信息到图片中
def embed_info(image_path, message, output_path):
    # 把中文转换为base64编码
    message = base64.b64encode(message.encode('utf-8')).decode('ascii')
    secret = lsb.hide(image_path, message)
    secret.save(output_path)

# 从图片中提取信息
def extract_info(image_path):
    secret_message = lsb.reveal(image_path)
    # 把base64编码还原为中文
    secret_message = base64.b64decode(secret_message.encode('ascii')).decode('utf-8')
    return secret_message

...

运行结果：

原图：

嵌入信息后的图：

两张图片大小一样，看不出任何差异，因为嵌入的信息量相对于图像的大小很小，只占了0.02%左右（24字节/1228800字节）。

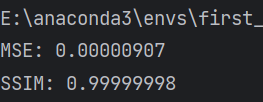
比较两张图片的差异，有多种方法和指标，比如均方误差（MSE）、结构相似性指数（SSIM）等。这些方法都是基于图片的像素值来计算两张图片之间的差异程度，差异越小，说明图片越相似。

代码：

...

# 定义MSE函数
def mse(imageA, imageB):
    # 计算两张图片之间的均方误差
    # 两张图片必须有相同的尺寸
    err = np.sum((imageA.astype("float") - imageB.astype("float")) ** 2)
    err /= float(imageA.shape[0] * imageA.shape[1])

    # 返回MSE值，越小越相似
    return err

...

结果：

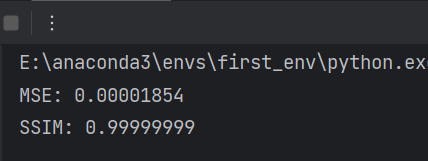
可见，嵌入“深圳杯数学建模挑战赛”后，两张图片的差异非常非常小。

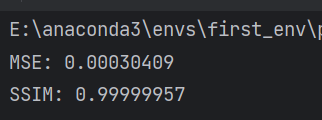
把题目第二段文字也嵌入图片时，差异变大了一丢丢。

2.12 LSB 方法建模

上面的方法说明，使用lsb方法将信息嵌入图片的做法是可行的。因此我们建立lsb方法的数学模型，通过lsb方法的原理进行编程。

由于题目给的图片是jpg格式，所以本节模型和代码支持原始图片的jpg格式输入。

但是，对jpg原始图片嵌入信息后，不能再保存为jpg格式，因为jpg无法保证完全不丢失细节，这样会对嵌入的信息进行扰乱，所以输出时要无损保存为PNG格式，这样就可以完整记录图片每个像素点rgb值的情况。

数学模型：

这两个函数的基本原理是利用了图像的最低有效位（Least Significant Bit，LSB）来嵌入和提取信息。这种方法是一种简单的隐写术技术，通过修改图像像素的最低有效位来嵌入信息，因为这种修改对图像的视觉效果影响很小，几乎无法察觉。

以下是这两个函数的数学模型：

1. 嵌入信息 :

   对于每个字符 c 在消息 message 中，将其转换为8位二进制表示 b(c)。然后，遍历图像的每个像素 (r, g, b)，并将每个颜色通道的最低有效位替换为 b(c) 的一个位。这可以用以下公式表示：

   $$...$$ $$...$$ $$...$$

   其中 r', g', b' 是新的像素值，b(c)_i 是 b(c) 的第 i 位，mod 是模运算。
   

2. 提取信息：

   遍历图像的每个像素 (r, g, b)，并从每个颜色通道的最低有效位中提取信息位。然后，将这些信息位组合成8位二进制表示，转换为字符。这可以用以下公式表示：

   $$b(c{)}_i=rmod2$$ $$...$$$$b(c{)}_{i+2}=bmod2$$
   其中 b(c)_i 是 b(c) 的第 i 位，mod 是模运算。然后，我们将 b(c) 转换为字符 c。

---

代码：

# -*- coding: UTF-8 -*-

...
# 嵌入信息到图片中
def embed_info(image_path, message, output_path):
    # 把中文转换为base64编码
    message = base64.b64encode(message.encode('utf-8')).decode('ascii')
    # 把信息转换为二进制位
    bits = ''.join(format(ord(x), '08b') for x in message)
    info_len = len(bits)
    # 打开图片
    img = Image.open(image_path)
    # 获取图片的宽度和高度
    width, height = img.size
    # 获取图片的像素数据
    pixels = img.load()
    # 初始化索引
    index = 0
    # 遍历每个像素
    for x in range(width):
        for y in range(height):
            # 获取当前像素的RGB值
            r, g, b = pixels[x, y]
            # 如果还有未嵌入的信息位
            if index < info_len:
                # 把当前像素的红色分量的最低有效位替换为信息位
                r = int(format(r, '08b')[:-1] + bits[index], 2)
                # 索引加一
                index += 1
            # 如果还有未嵌入的信息位
            if index < info_len:
...

信息解析检验：

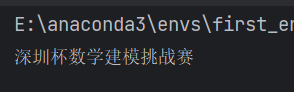
相似度检验：均方误差比使用库低，结构相似性指数则稍高一点点，依旧是肉眼无法分辨。

输出图片：

2.2 问题二

结果是可以的。

原因：

• 原始图片的尺寸是1280*1896。按照本文的lsb模型，可以用来存储信息的二进制位总共有：3 * 1280*1896个。
• 本文将《中华人民共和国著作权法》保存为txt文件，大小为33KB，在模型中经过编码转换，最终使用349952个二进制位来表示。
• 要隐藏的信息的二进制位数远远小于图片可供存储的位数。所以可以将所有文字信息嵌入附件1的图片中。

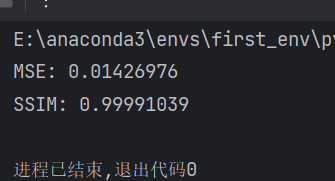
信息嵌入效果：

图片前后差异：

2.3 问题三

前面的lsb方法是很有效的，对图像的视觉影响极小。

但是，当出现图像被压缩或以不同的图片格式存储，也可能会被缩放、旋转或其他几何变形等情况时。

前面的信息嵌入算法就不能从图片中提取出嵌入的信息了。（因为这些操作可能会改变像素值的最低有效位，从而破坏嵌入的信息）

因此，需要对算法进行改进。

2.31 方法与步骤概述

可以采用一种称为"鲁棒"的信息隐藏技术。鲁棒信息隐藏技术的目标是在图像处理（如压缩、缩放、旋转等）后仍能提取出隐藏的信息。以下是一些可能的改进方法：

1. 使用更复杂的嵌入技术：例如，使用离散余弦变换（DCT）或离散小波变换（DWT）等频域方法进行信息嵌入。这些方法将信息隐藏在图像的频域中，而不是像LSB那样直接在空间域中隐藏。这样，即使图像经过一些处理，隐藏的信息也能被提取出来。

2. 使用错误纠正编码：例如，使用汉明码或里德-所罗门码等错误纠正编码对隐藏的信息进行编码。这样，即使图像处理过程中一部分信息被破坏，也能通过错误纠正编码恢复出原始信息。

3. 使用水印技术：水印是一种特殊的信息隐藏技术，它的目标是在图像中隐藏一个标识符，即使图像经过处理，这个标识符也能被检测出来。水印技术通常使用一些复杂的嵌入和提取算法，以提高鲁棒性。

4. 使用更强大的机器学习方法：例如，使用深度学习进行信息隐藏和提取。深度学习可以学习到如何在不同的图像处理操作下保持信息的隐藏和提取，从而提高鲁棒性。

以上这些方法都可以提高信息隐藏技术的鲁棒性，但也需要注意，提高鲁棒性通常会牺牲一些隐藏信息的容量。不过在用于保护著作权时，需要往图片中嵌入的信息也不会很多。

本文使用水印技术进行信息嵌入（暗水印，肉眼不可见）。

---

主要步骤为：

1. 生成水印图片（正方形）；
   • 根据文本长度计算合适的行数；
   • 创建空白图片；
   • 在图片上绘制文本；
   • 保存图片。
   • …
2. 嵌入水印；
   • …
   • …
   • 对…
3. 提取水印。
   • 将嵌入水印的图片尽可能恢复到与原始图片相近的状态（针对旋转、裁剪和缩放）；
   • …
   • …；
   • 对提取的水印图片进行Arnold逆变换（如果嵌入的黑丝经过Arnold变换后的水印图片）。

2.32 基于DCT的暗水印信息嵌入模型

2.32 - 1 水印图片生成

主要代码：

def create_watermark(text, font_path, font_size=26, opacity=100):
    # Calculate lines
    n = int(math.sqrt(len(text))) + 1
    lines = [text[i:i + n] for i in range(0, len(text), n)]
    # Create a blank image with white background
    width, height = n * font_size, n * font_size
    img = Image.new('RGBA', (width, height), (255, 255, 255))
    # Load font
    font = ImageFont.truetype(font_path, font_size)
    # Initialize ImageDraw
    draw = ImageDraw.Draw(img)
    # Set text color
    text_color = (0, 0, 0, opacity)
    # Draw text on image
    for i, line in enumerate(lines):
        # Calculate the width of the line
        text_bbox = draw.textbbox((0, 0), line, font)
        line_width = text_bbox[2] - text_bbox[0]
        # Calculate the x coordinate to center the line
        x = (width - line_width) / 2
        draw.text((x, i * font_size), line, font=font, fill=text_color)
    # Save the image
    img.save('watermark.png', 'PNG')

水印图片：

2.32 - 2 水印图片 Arnold置乱

即打乱水印信息，使得信息分布均匀，减小可能得损失，同时防止水印被他人提取和篡改。

Arnold置乱是一种图像加密技术，它是由V.I. Arnold提出的一种二维图像的置乱变换方法。它的基本思想是将图像看作是在二维整数平面上的一个函数，然后通过一定的几何变换，将原图像的像素位置进行置乱，从而达到图像加密的目的。

Arnold置乱的基本公式如下：

对于图像中的每一个像素点(x, y)，经过Arnold置乱后，该像素点的新位置(x’, y’)可以通过以下公式计算得到：

$$...$$$$y^{\prime }=(x+2y)modN$$

其中，N是图像的宽度或高度（假设图像是正方形的），mod是取模运算。

Arnold置乱的逆操作，也就是解密过程，可以通过以下公式进行：

$$x=(2x^{\prime }-y^{\prime })modN$$$$y=...$$

这两组公式就是Arnold置乱及其逆操作的基本公式。通过这两组公式，可以实现图像的加密和解密操作。

---

效果：

部分代码：

# 对水印图片进行 Arnold 置乱
def arnold_scramble(image, iterations):
    # Convert the image to a numpy array
    array = np.array(image)
    # Get the size of the image
    height, width, _ = array.shape
    # Create an empty array to hold the scrambled image
    scrambled_array = np.empty_like(array)
    # Perform the scrambling
    for _ in range(iterations):
        for y in range(height):
            for x in range(width):
                scrambled_array[x,y] = array[(x + y) % height, (x + 2 * y) % width]
        array = scrambled_array.copy()
    # Convert the scrambled array back to an image
    scrambled_image = Image.fromarray(np.clip(scrambled_array, 0, 255).astype('uint8'))

    return scrambled_image

2.32 - 2 水印嵌入

本文使用的是基于DCT的暗水印技术。即将水印图片嵌入到图片的频域而不是前面LSB的空域。

在离散余弦变换（DCT）的结果中，低频部分通常包含了图像的大部分信息，如颜色和亮度变化。这是因为图像的大部分区域通常有相似的颜色和亮度，这些信息在频域中表现为低频成分。因此，你可以看到在DCT图像的左上角（低频部分）有更多的亮点。

相反，高频部分包含了图像的细节和纹理信息，如边缘和纹理。这些信息在频域中表现为高频成分。因此，你可以看到在DCT图像的右下角（高频部分）有一些亮点，但通常比低频部分少。

中频部分则介于两者之间，包含了一些颜色和亮度的变化，以及一些细节和纹理信息。

在图像的频域表示中，高频部分通常包含的信息最少。这是因为…

相反，…

因此，中频部分通常被认为是嵌入水印的最佳位置。 中频部分包含了一些颜色和亮度的变化，以及一些细节和纹理信息，因此在这个部分嵌入水印不太可能显著改变图像的视觉效果。同时，由于中频部分的信息在图像压缩或降低分辨率时不太可能被丢弃，因此在这个部分嵌入的水印也更有可能保留下来。

因此，本文即是将水印嵌入图像在DCT变换后的中频部分。

---

当然，以下是离散余弦变换（DCT）的公式。

对于一维信号，DCT的公式如下：

对于长度为N的实数序列x(n)，其DCT变换为X(k)，计算公式为：

$$...$$

其中，n=0,1,…,N-1；k=0,1,…,N-1。

对于二维图像，我们可以将其看作是两个方向（x和y）上的信号，因此可以对每个方向分别进行DCT变换。首先在一方向（例如，行）上对所有信号进行DCT变换，然后在另一方向（例如，列）上对所有信号进行DCT变换。这样，我们就得到了二维DCT变换。

二维DCT的公式如下：

$$F(u,v)=C(u)C(v)/4\ast su{m}_{x=0}^{M-1}su{m}_{y=0}^{N-1}f(x,y)cos[(2x+1)u\ast pi/2M]cos[(2y+1)v\ast pi/2N]$$

其中，x和y是图像的坐标，M和N是图像的宽度和高度，F(u,v)是频域上的值，f(x,y)是时域上的值，u和v是频率。C(u)和C(v)是归一化系数，当u或v为0时，C(u)或C(v)为1/√2，否则为1。

这些公式都是基于余弦函数，这就是为什么它被称为“离散余弦变换”。

对于一维信号，逆DCT的公式如下：

对于长度为N的实数序列X(k)，其逆DCT变换为x(n)，计算公式为：

$$x(n)=su{m}_{k=0}^{N-1}X(k)cos[(pi/N)(n+1/2)k],n=0,1,...,N-1$$

其中，n=0,1,…,N-1；k=0,1,…,N-1。

对于二维图像，我们可以将其看作是两个方向（u和v）上的信号，因此可以对每个方向分别进行逆DCT变换。首先在一方向（例如，行）上对所有信号进行逆DCT变换，然后在另一方向（例如，列）上对所有信号进行逆DCT变换。这样，我们就得到了二维逆DCT变换。

二维逆DCT的公式如下：

$$...$$

其中，x和y是图像的坐标，M和N是图像的宽度和高度，F(u,v)是频域上的值，f(x,y)是时域上的值，u和v是频率。C(u)和C(v)是归一化系数，当u或v为0时，C(u)或C(v)为1/√2，否则为1。

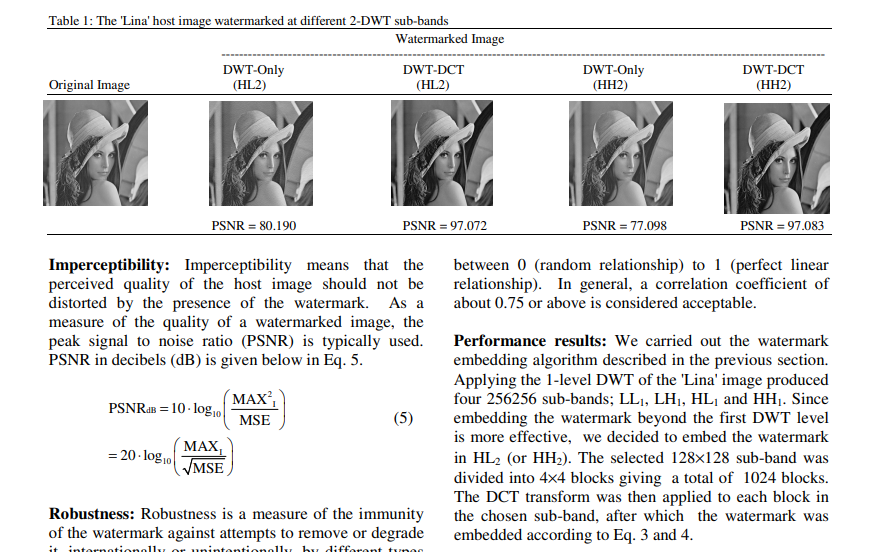
效果演示：

alpha=0.1

alpha = 0.9

部分代码：

# 对原始图像执行离散余弦变换（DCT）
def perform_dct(original_array):
    height, width, _ = original_array.shape
    dct_blocks = np.empty_like(original_array, dtype=np.float64)
    for i in range(0, height, 8):
        for j in range(0, width, 8):
            dct_blocks[i:i + 8, j:j + 8] = dct(dct(original_array[i:i + 8, j:j + 8], axis=0, norm='ortho'), axis=1,
                                               norm='ortho')
    return dct_blocks


# 将水印嵌入到DCT块中
def embed_watermark(dct_blocks, watermark_array, alpha=0.05):
    dct_blocks_with_watermark = dct_blocks.copy()
    dct_blocks_with_watermark[::8, ::8] += alpha * watermark_array
    return dct_blocks_with_watermark

2.32 - 3 水印提取

第一种情况针对被旋转图片进行水印信息的提取，首先通过Canny算子实现边缘提取，再使用Hough变换对图像进行几何形状检测，通过合理设置阈值筛选出合适的旋转角度并将其恢复水平。最后裁剪掉无效的图像边框得到的图片即可进行提取水印操作。

第二种情况针对被裁剪图片进行水印信息的提取，将…。

第三种情况针对被缩放的图片，通过…提供的zoom操作函数得到的图片即可进行提取水印操作。

提取水印的过程中，首先需要将图片再次进行8×8分块，再对子块进行水印的提取。由于在之前的操作中对水印图片进行了加密置乱，故在此处需要进行Arnold逆变换来实现水印信息的解密复原，最终提取出一张水印图片。

效果：

部分代码：

def process_images(image_with_watermark_path, original_image_path, alpha=0.05):
    # 加载图像
    image_with_watermark = load_image(image_with_watermark_path)
    original_image = load_image(original_image_path)
    # 将图像转换为数组
    image_with_watermark_array = image_to_array(image_with_watermark)
    original_array = image_to_array(original_image)
    # 对图像执行DCT
    dct_blocks_with_watermark = perform_dct(image_with_watermark_array)
    original_dct_blocks = perform_dct(original_array)
    # 提取水印
    watermark_array = extract_watermark(dct_blocks_with_watermark, original_dct_blocks, alpha)
    # 裁剪和转换图像
    watermark_array = clip_and_convert(watermark_array)
    # 将数组转换回图像
    watermark_image = array_to_image(watermark_array)
    return watermark_image

2.4 问题四

LSB（Least Significant Bit）是一种常见的信息隐藏技术，通常用于数字水印和隐写术。在使用LSB进行信息嵌入时，需要注意以下几点：

1. 选择合适的嵌入位置：LSB通常是将信息嵌入到图像的最低有效位，因为这样对图像的影响最小，人眼难以察觉。然而，如果图像可能会受到压缩或其他形式的处理，这些处理可能会改变最低有效位，导致嵌入的信息丢失。因此，如果预计图像可能会受到这种处理，可能需要选择其他的嵌入位置，例如更高的位。

2. 保护嵌入信息的安全性：虽然LSB嵌入可以隐藏信息，但如果攻击者知道使用了LSB嵌入，他们可能会尝试提取或破坏这些信息。因此，可能需要使用加密或其他形式的保护来确保嵌入信息的安全性。（比如先对要嵌入的信息进行加密再进行嵌入）

3. 避免过度嵌入：虽然LSB嵌入对图像的影响较小，但如果嵌入的信息过多，可能会导致图像质量明显下降。因此，需要在隐藏信息的需要和保持图像质量之间找到平衡。

三、参考文献

很多内容都是参考的这些文献，算是一些方法的复现和综合吧。写论文的时候，相关概念、公式都可以参考这些文献。（不过我也给出了很多概念及其公式）

所有：

部分预览：

四、代码预览