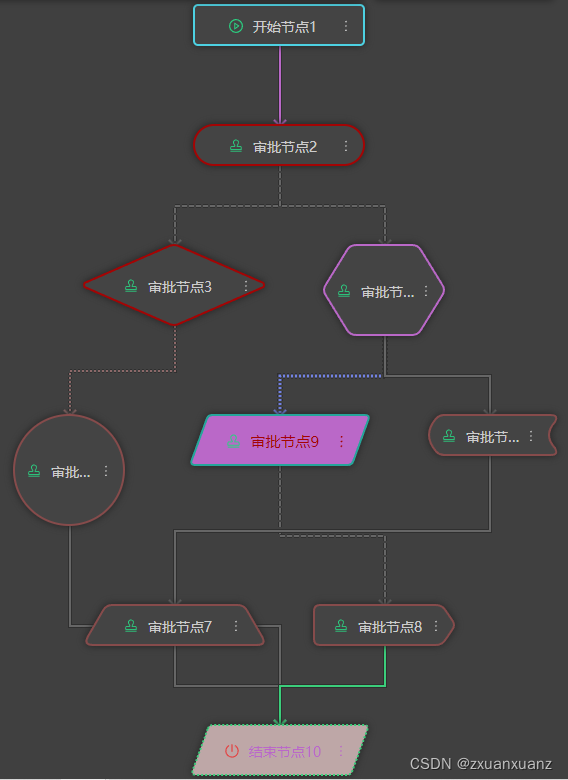
一、背景
(1)流程节点为矩形,只有上下左右四个连接点。
(2)支持移动,放大缩小,连接线。

二、需求
(1)流程节点支持图形变化。
(2)支持节点边框样式设置。
(3)图形支持圆角
三、方案设计
(1) 根据开发成本考虑,仅支持仍为四个操作点(上、下、左、右)的图形。这样线的连接,绘制操作等原本根据矩形编写的逻辑都不用重新编写,能够保持一致的逻辑。支持:矩形、圆角矩形、菱形、正六边形、平行四边形,圆形,梯形,以及两个不规则图形。
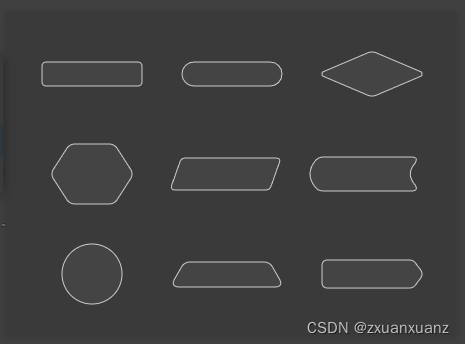
(2)保持原本矩形四个连接点、以及其他逻辑
1、矩形作为固定层,无边框任然存在,将svg图形和矩形同时绘制并重叠,svg图形展示边框,但是操作点的位置,操作栏任然根据矩形去计算。(实际还是矩形,只是图形展示使用svg去绘制展示了)以圆形为例:
矩形:

svg
2、svg图形上的点是要根据矩形去计算的。计算出来的svg可能是会超出矩形。例如:梯形和平行四边形。并且需要支持放大缩小,因此svg图形上的点需要根据矩形的宽高去计算。
矩形:

svg
大致:
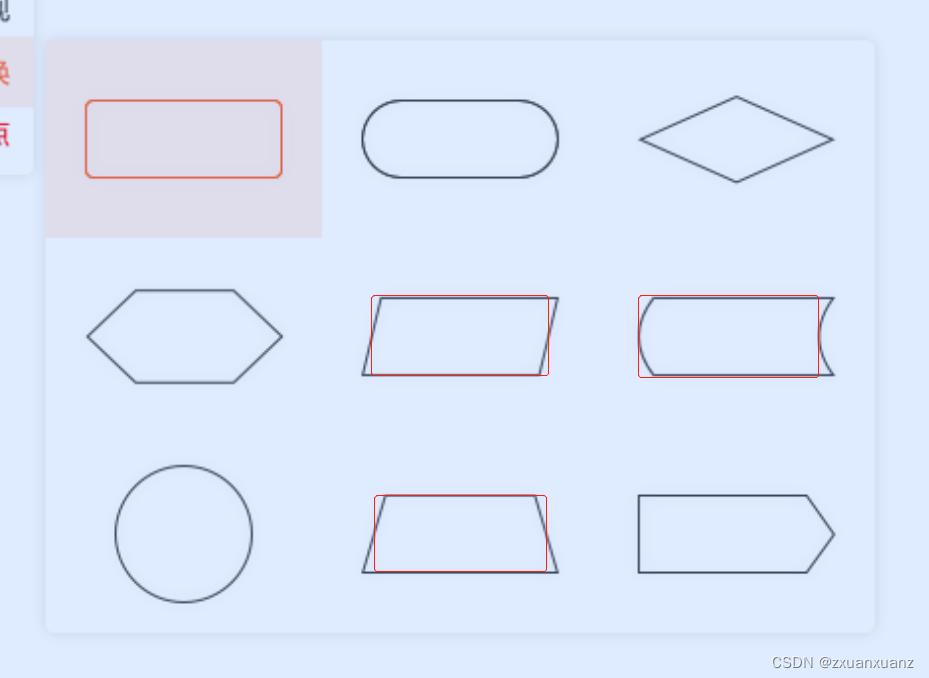
3、因为svg超出范围无法显示,故需要对svg背景做一个根据矩形的一个偏移,将矩形的四个点放置在svg图形上。
(3)缩放图标的位置根据图形要做调整,例如梯形,因为原本缩放图标的位置是根据矩形计算的,一些超出矩形的图形还是根据矩形计算的话会出现距离上的问题,因此需要根据具体svg图形做一个调整。
未调整:
调整:
(4)图形弧形弧度和角度要考虑
因为不同的角度计算出来的图形形状是不一样的,因为需要跟UI沟通好
(5)keepLength根据图形去调整
此属性是绘制线,线开段的那段长度,不同图形可能会出现挡住,过短的情况,因此要根据具体图形做调整。
(6)svg阴影
1、有=》无阴影区别
2、方案
a、可以采用svg方案,filter
<defs>
<filter
id="outset-shadow"
height="150%"
width="150%"
x="-25%"
y="-25%"
filterUnits="userSpaceOnUse"
>
<feMorphology
operator="dilate"
radius="3"
in="SourceAlpha"
result="thicken"
/>
<feGaussianBlur in="thicken" stdDeviation="3" result="blurred" />
<feFlood flood-color="grey" result="glowColor" />
<feComposite
in="glowColor"
in2="blurred"
operator="in"
result="softGlowColored"
/>
<feComposite
in="softGlowColored"
in2="SourceGraphic"
operator="out"
result="outSoftGlowColored"
/>
<feMerge>
<feMergeNode in="outSoftGlowColored" />
<feMergeNode in="SourceGraphic" />
</feMerge>
</filter>
</defs>
<defs>
<filter id="blur" filterUnits="userSpaceOnUse">
<feOffset result="offset" in="SourceAlpha" />
<feGaussianBlur result="blur" stdDeviation="5" />
<feFlood result="flood" flood-color="#eee" />
<feComposite result="composite" operator="in" in2="blur" />
<feBlend result="blend" in="SourceGraphic" />
</filter>
</defs>b、 也可以采用css属性
filter: drop-shadow(0px 0px 4px var(--shadow))本方案采用的是简洁的css属性。
(7)样式根据svg提供的去实现即可。其中宽度,需要对图形的坐标做一个偏移(边框宽度的偏移)才能完整展示出来宽度。
三、svg图形绘制
(1)分析图形,发现图形很多都是对称图形,因此可以进行对称点计算
1、获取点关于直线的对称点坐标
/** @name 获取点关于直线的对称点坐标 */
export function getPointSymmetryPoint(
point,
symmetryLine = {
A: 0,
B: 0,
C: 0,
},
) {
const { A, B, C } = symmetryLine;
const x =
point.x -
(2 * A * (A * point.x + B * point.y + C)) /
(Math.pow(A, 2) + Math.pow(B, 2));
const y =
point.y -
(2 * B * (A * point.x + B * point.y + C)) /
(Math.pow(A, 2) + Math.pow(B, 2));
return {
x,
y,
};
}2、获取两点的中点坐标
/** @name 获取两点的中点坐标 */
export function getMiddlePoint(point1, point2) {
return {
x: (point1.x + point2.x) / 2,
y: (point1.y + point2.y) / 2,
};
}3、弧形,绘制二次贝尔曲线,需要求控制点(已知起点、终点、中点求控制点),此公式在绘制正六边形、弧形矩形、菱形、右直角矩形中会用到,因为需要弧形的顶点落在矩形上。
/** @name 已知起点、终点、中点求控制点 */
export function threePointGetControlPoint(sPoint, ePoint, mPoint) {
const x = 2 * mPoint.x - (sPoint.x + ePoint.x) / 2;
const y = 2 * mPoint.y - (sPoint.y + ePoint.y) / 2;
return { x, y };
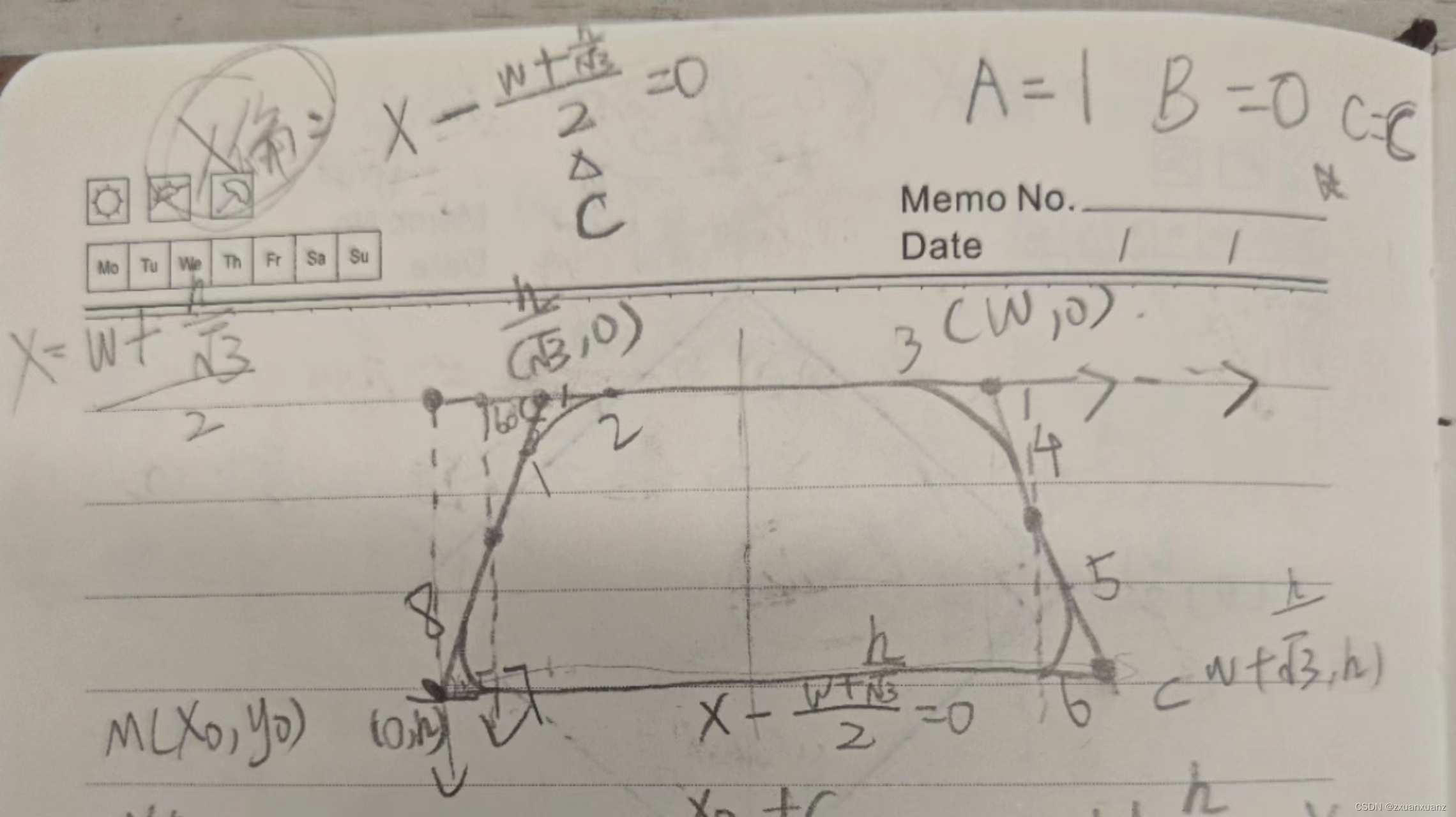
}(2)节点宽高是已知,根据节点宽高,图形的角度,根据三角函数去画图计算点坐标,对称点根据函数去计算,弧形使用二次贝尔曲线绘制(弧形的起点、终点,终点需要进行假设)。以梯形为例:
<template>
<g>
<path
:style="computedStyle"
:class="computedClass"
class="node-figure"
:d="path"
/>
<foreignObject
:x="levelPoint.x"
:y="levelPoint.y"
class="flower-node-level"
v-if="level && showLevel"
>
<span>{{ level }}</span></foreignObject
>
</g>
</template><script>
import { Vue, Component, Prop } from 'vue-property-decorator';
import { getPointSymmetryPoint } from './utils.js';
@Component()
//梯形
export default class LadderShaped extends Vue {
/** @type { number } */
@Prop() width;
/** @type { number } */
@Prop() height;
/** @type { boolean } */
@Prop({ type: Object, default: () => ({}) }) borderStyle;
@Prop({ type: Number, default: 1 }) level;
@Prop({ type: Object, default: () => ({}) }) computedStyle;
@Prop({ type: Array, default: () => [] }) computedClass;
@Prop({ type: Boolean, default: false }) showLevel;
get offset() {
if (!this.borderStyle) return 1;
return Number(this.borderStyle.width);
}
get levelPoint() {
const tan = Math.tan((this.angle * Math.PI) / 180);
const control12 = this.handleOffsetPoint({
x: this.height / tan - 5,
y: -1,
});
return control12;
}
angle = 60;
get topXOffset() {
return 6;
}
get bottomXOffset() {
return 10;
}
get path() {
//tan60值
const tan = Math.tan((this.angle * Math.PI) / 180);
const sin = Math.sin((this.angle * Math.PI) / 180);
const cos = Math.cos((this.angle * Math.PI) / 180);
const point1 = this.handleOffsetPoint({
x: this.height / tan - cos * this.topXOffset,
y: sin * this.topXOffset,
});
const point2 = this.handleOffsetPoint({
x: this.height / tan + this.topXOffset,
y: 0,
});
const point7 = this.handleOffsetPoint({
x: this.bottomXOffset,
y: this.height,
});
const point8 = this.handleOffsetPoint({
x: this.bottomXOffset * cos,
y: this.height - this.bottomXOffset * sin,
});
//计算对称点
const line = {
A: 1,
B: 0,
C: -((this.width + this.height / tan) / 2) - this.offset,
};
const point3 = getPointSymmetryPoint(point2, line);
const point4 = getPointSymmetryPoint(point1, line);
const point5 = getPointSymmetryPoint(point8, line);
const point6 = getPointSymmetryPoint(point7, line);
const control12 = this.handleOffsetPoint({
x: this.height / tan,
y: 0,
});
const control34 = this.handleOffsetPoint({
x: this.width,
y: 0,
});
const control56 = this.handleOffsetPoint({
x: this.width + this.height / tan,
y: this.height,
});
const control78 = this.handleOffsetPoint({
x: 0,
y: this.height,
});
return `M ${point1.x} ${point1.y}
Q ${control12.x} ${control12.y} ${point2.x} ${point2.y}
L ${point3.x} ${point3.y}
Q ${control34.x} ${control34.y} ${point4.x} ${point4.y}
L ${point5.x} ${point5.y}
Q ${control56.x} ${control56.y} ${point6.x} ${point6.y}
L ${point7.x} ${point7.y}
Q ${control78.x} ${control78.y} ${point8.x} ${point8.y}
Z`;
}
handleOffsetPoint({ x, y }) {
return { x: x + this.offset, y: y + this.offset };
}
}
</script>
<style lang="less"></style>
四、svg相关知识
(1)基础图形
1、矩形(圆角)
<rect
width="200"
height="100"
rx="20"
ry="40"
>2、 圆形
<circle
cx="60"
cy="80"
r="50"
>3、 path
<path
d="M 10 10 L 50 40 L 100 10"
stroke="blue"
fill="none"
>
- M: 起始点坐标,
moveto的意思。每个路径都必须以M开始。M传入x和y坐标,用逗号或者空格隔开。L: 轮廓坐标,lineto的意思。L是跟在M后面的。它也是可以传入一个或多个坐标。大写的L是一个绝对位置。- l: 这是小写
L,和L的作用差不多,但l是一个相对位置。H: 和上一个点的Y坐标相等,是horizontal lineto的意思。它是一个绝对位置。h: 和H差不多,但h使用的是相对定位。V: 和上一个点的X坐标相等,是vertical lineto的意思。它是一个绝对位置。v: 这是一个小写的v,和大写V的差不多,但小写v是一个相对定位。Z: 关闭当前路径,closepath的意思。它会绘制一条直线回到当前子路径的起点
(2)图形样式设置方法
1、属性样式:直接在元素属性上设置样式
<rect
x="100"
y="100"
width="200"
height="100"
fill="pink"
/>2、 内联样式:把所有样式写在 style 属性里
<rect
x="100"
y="100"
width="200"
height="100"
style="fill: pink;"
/>3、 内部样式:将样式写在 <style> 标签里
<style>
.rect {
fill: pink;
}
</style>
<svg width="400" height="400" style="border: 1px solid red;">
<rect
x="100"
y="100"
width="200"
height="100"
class="rect"
/>
</svg>
4、外部样式:将样式写在 .css 文件里,然后在页面中引入该 CSS 文件
(3)使用的样式设置
1、填充 fill:要填充图案颜色,可以设置 fill 属性
<rect
x="100"
y="100"
width="200"
height="100"
fill="greenyellow"
/>2、 描边颜色 stroke
<rect
x="100"
y="100"
width="200"
height="100"
fill="none"
stroke="blue"
/>3、 描边宽度 stroke-width
<rect
x="100"
y="100"
width="200"
height="100"
fill="none"
stroke="blue"
stroke-width="10"
/>4、 虚线描边 stroke-dasharray
边框的点线或者虚线样式,stroke-dasharray 接收一串数字,这串数字可以用来代表线的长度和空隙的长度,数字之间用逗号或者空格分隔。建议传入偶数个数字。但如果你传入了奇数个数字,SVG 会将这串数字重复一遍,使它的数量变成偶数个
<line
x1="30"
y1="70"
x2="300"
y2="70"
stroke="blue"
stroke-dasharray="20 10"
/>5、线帽 stroke-linecap:线帽就是线的起始点和结束点的位置
butt: 平头(默认值)round: 圆头square: 方头
6、拐角 stroke-linejoin:拐角就是折线的交接点
miter: 尖角(默认)round: 圆角bevel: 平角
(4)曲线
Q命令可以用来绘制一条二次贝塞尔曲线,二次贝塞尔曲线需要一个控制点,用来确定起点和终点的曲线斜率。
Q x1 y1, x y 或者 q x1 y1, x y
1、参数:x、y为终点位置,x1、y1为控制点
2、起点就是M命令
<path d="M50 100 Q 175 200 300 100" fill="none" style="stroke: #ff0000;"/>五、效果图