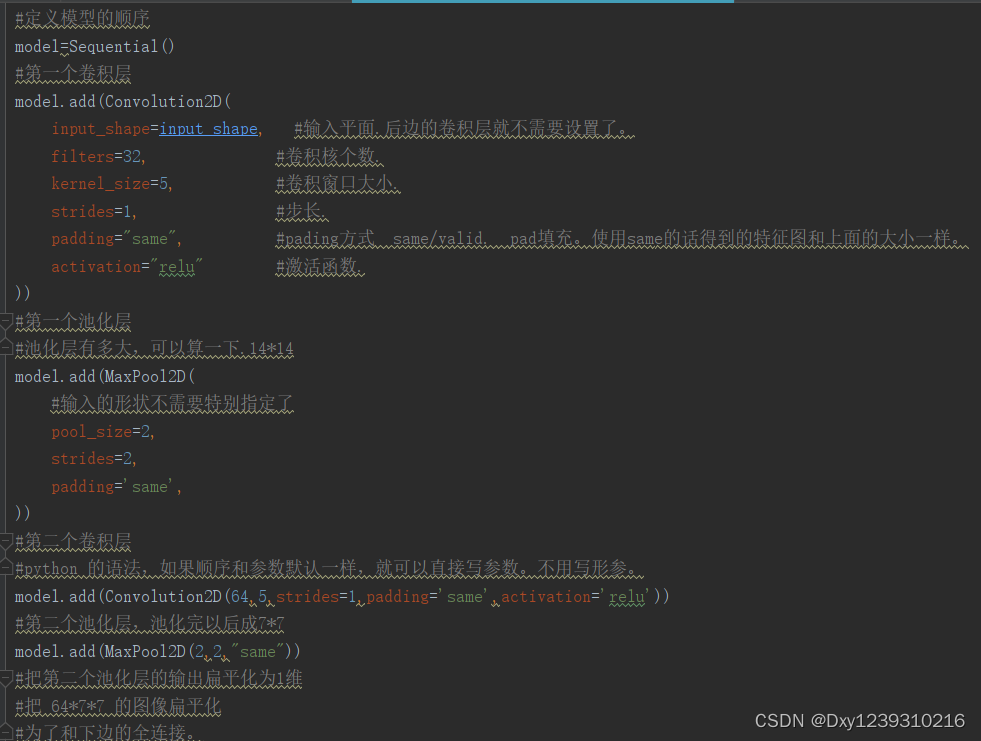
目录
一、基本概念
1.1 什么是信息熵?
1.2 决策树的定义与构造
二、决策树算法
2.1 ID3 决策树
2.2 C4.5 决策树
2.3 CART 决策树
一、基本概念
1.1 什么是信息熵?
信息熵:
熵是度量样本集合纯度最常用的一种指标,代表一个系统中蕴含多少信息量,信息量越大表明一个系统不确定性就越大,就存在越多的可能性,即信息熵越大。

1.2 决策树的定义与构造
决策树是一种基于树形结构来进行决策的算法,它的主要原理是将数据集划分为一系列小的子集,每个子集称为一个决策树的“节点”,决策树的分支表示不同的决策路径,叶节点表示最终的决策结果。
在决策树的建立过程中,通常采用的是自顶向下的贪心策略,即每次选择最优的划分特征来进行节点的分裂,直到满足停止条件为止。
在选择最优的划分特征时,需要使用一些评估指标,如信息增益、基尼指数等来评估每个特征的划分能力,并选择具有最大划分能力的特征作为节点的分裂特征。
一般的,一棵决策树包含一个根结点、若干个内部结点和若干个叶结点;
叶结点对应于决策结果,其他每个结点则对应于一个属性测试:
每个结点包含的样本集合根据属性测试的结果被划分到子结点中
根结点包含样本全集.从根结点到每个叶结点的路径对应了一个判定测试序列,决策树学习的目的是为了产生一棵泛化能力强,即处理未见示例能力强的决策树,其基本流程遵循简单的“分而治之”

最关键的在第 8 行
如何选择最优划分属性

决策树的构造是一个递归的过程,有三种情形会导致递归返回:
(1) 当前结点包含的样本全属于同一类别,这时直接将该节点标记为叶节点,并设为相应的类别
对应第 2 行的 if 语句
(2) 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分,这时将该节点标记为叶节点,并将其类别设为该节点所含样本最多的类别;
对应第 5 行的 if 语句
(3) 当前结点包含的样本集合为空,不能划分,这时也将该节点标记为叶节点,并将其类别设为父节点中所含样本最多的类别。
对应第 11 行的 if 语句
二、决策树算法
2.1 ID3 决策树
ID3 决策树使用信息增益为准则来选择划分属性
信息增益: 在已知属性 (特征)a的取值后的不确定性减少的量,也即纯度的提升
信息熵 度量随机变量 X 的不确定性 越大越不确定!




信息增益越大,表示使用该属性划分样本集D的效果越好
因此ID3算法在递归过程中,每次选择最大信息增益的属性作为当前的划分属性
举例:
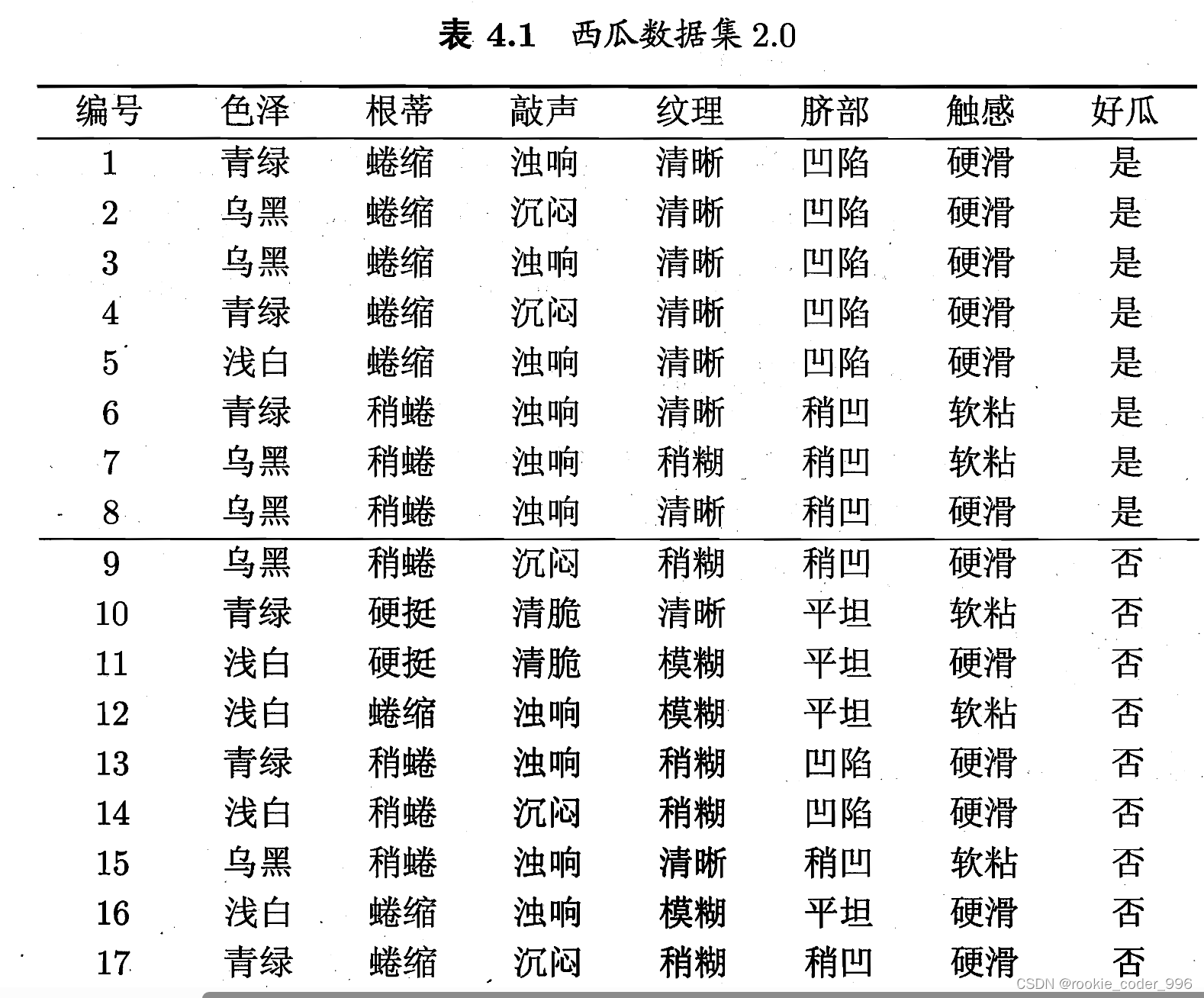


显然,属性“纹理”的信息增益最大,于是它被选为划分属性
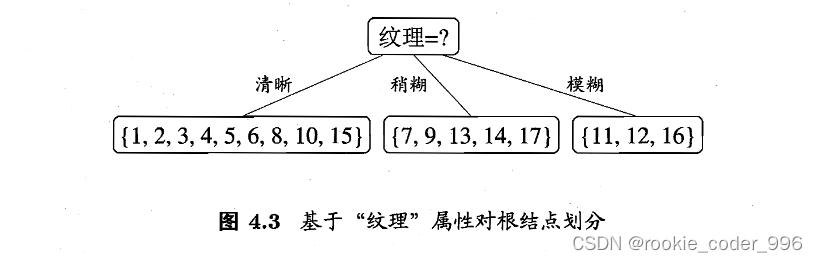
划分结果:
2.2 C4.5 决策树
ID3算法存在一个问题,就是偏向于取值数目较多的属性,例如:如果存在一个唯一标识,这样样本集D将会被划分为|D|个分支,每个分支只有一个样本,这样划分后的信息熵为零,十分纯净,但是对分类毫无用处。
因此C4.5算法使用了“增益率”(gain ratio)来选择划分属性,来避免这个问题带来的困扰。

C4.5决策树并未完全使用“增益率”代替“信息增益”,而是采用一种启发式的方法先选出信息增益高于平均水平的属性,然后再从中选择增益率最高的。
首先使用ID3算法计算出信息增益高于平均水平的候选属性,接着C4.5计算这些候选属性的增益率。
2.3 CART 决策树
CART决策树使用“基尼指数”(Gini index)来选择划分属性,基尼指数反映的是从样本集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小越好,越小表明碰到的异类的概率越小,纯度就越高


基尼指数越小,表明集合越纯
选择基尼指数最小的属性作为最优划分属性