代码来自闵老师”日撸 Java 三百行(51-60天)“,链接:https://blog.csdn.net/minfanphd/article/details/116975957
相较于符号型数据,数值型是将实例的概率密度带入进行概率计算。数值型数据仅需要对决策属性那里进行Laplacian平滑处理即可。
用正态分布求得概率密度在实际中最常见,公式如下:
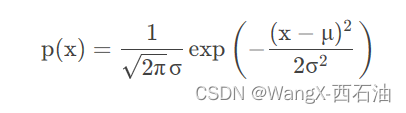
这里涉及两个参数: 方差 和均值
,可以计算出来。去掉常数,优化目标为:
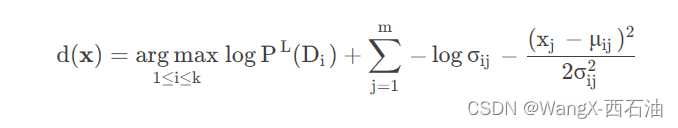
代码实现如下:
package datastructure.nb;
import java.io.FileReader;
import java.util.Arrays;
import weka.core.Instance;
import weka.core.Instances;
/**
* ********************************************
* The Naive Bayes algorithm.
*
* @author WX873
**********************************************
*/
public class NaiveBayes {
/**
*************************
* An inner class to store parameters.
* @author WX873
*************************
*/
private class Gaussianparamters{
double mu;
double sigma;
public Gaussianparamters(double paraMu, double paraSigma) {
// TODO Auto-generated constructor stub
mu = paraMu;
sigma = paraSigma;
}//of the constructor
public String toString() {
return "(" + mu + ", " + sigma + ")";
} //of toString
}//of Gaussianparamters
/**
* The data.
*/
Instances dataset;
/**
* The number of classes. For binary classification it is 2.
*/
int numClasses;
/**
* The number of instances.
*/
int numInstances;
/**
* The number of conditional attributes.
*/
int numConditions;
/**
* The prediction, including queried and predicted labels.
*/
int[] predicts;
/**
* Class distribution.
*/
double[] classDistribution;
/**
* Class distribution with Laplacian smooth.
*/
double[] classDistributionLaplacian;
/**
* To calculate the conditional probabilities for all classes over all
* attributes on all values.
*/
double[][][] conditionalCounts;
/**
* The conditional probabilities with Laplacian smooth.
*/
double[][][] conditionalProbabilitiesLaplacian;
/**
* The Guassian parameters.
*/
Gaussianparamters[][] gaussianparamters;
/**
* Data type.
*/
int dataType;
/**
* Nominal
*/
public static final int NOMINAL = 0;
/**
* Numerical.
*/
public static final int NUMERICAL = 1;
/**
* **********************************************************
* The first constructor.
*
* @param paraFilename The given file.
* **********************************************************
*/
public NaiveBayes(String paraFilename) {
// TODO Auto-generated constructor stub
dataset = null;
try {
FileReader fileReader = new FileReader(paraFilename);
dataset = new Instances(fileReader);
fileReader.close();
} catch (Exception e) {
// TODO: handle exception
System.out.println("Cannot read the file: " + paraFilename + "\r\n" + e);
System.exit(0);
}//of try
dataset.setClassIndex(dataset.numAttributes() - 1);
numConditions = dataset.numAttributes() - 1;
numInstances = dataset.numInstances();
numClasses = dataset.attribute(numConditions).numValues();
}//The first constructor
/**
* **********************************************************
* The second constructor.
*
* @param paraInstances The instance of given file.
* **********************************************************
*/
public NaiveBayes(Instances paraInstances) {
// TODO Auto-generated constructor stub
dataset = paraInstances;
dataset.setClassIndex(dataset.numAttributes() - 1);
numConditions = dataset.numAttributes() - 1;
numInstances = dataset.numInstances();
numClasses = dataset.attribute(numConditions).numValues();
}//The second constructor
/**
* ****************************************************
* Set the data type.
* @param paraDataType
* ****************************************************
*/
public void setDataType(int paraDataType) {
dataType = paraDataType;
}//of setDataType
/**
* **************************************************************
* Calculate the class distribution with Laplacian smooth.
* **************************************************************
*/
public void calculateClassDistribution() {
classDistribution = new double[numClasses];
classDistributionLaplacian = new double[numClasses];
double[] tempCounts = new double[numClasses];
for (int i = 0; i < numInstances; i++) {
int tempClassValue = (int)dataset.instance(i).classValue();
tempCounts[tempClassValue]++;
}//of for i
for (int i = 0; i < numClasses; i++) {
classDistribution[i] = tempCounts[i]/numInstances;
classDistributionLaplacian[i] = (tempCounts[i] + 1)/(numInstances + numClasses);
}//of for i
System.out.println("Class distribution: " + Arrays.toString(classDistribution));
System.out.println("Class distribution Laplacian: " + Arrays.toString(classDistributionLaplacian));
}//of calculateClassDistribution
/**
* *****************************************************
* Calculate the conditional probabilities with Laplacian smooth.
* *****************************************************
*/
public void calculateConditionalProbabilities() {
conditionalCounts = new double[numClasses][numConditions][];
conditionalProbabilitiesLaplacian = new double[numClasses][numConditions][];
//Allocate space
for (int i = 0; i < numClasses; i++) {
for (int j = 0; j < numConditions; j++) {
int tempNumValues = (int)dataset.attribute(j).numValues(); //总共有多少个属性就申请多少个空间
conditionalCounts[i][j] = new double[tempNumValues];
conditionalProbabilitiesLaplacian[i][j] = new double[tempNumValues];
}//of for j
}//of for i
//Count the numbers of the same class and attribute.
int[] tempClassCounts = new int[numClasses];
for (int i = 0; i < numClasses; i++) {
int tempClass = (int)dataset.instance(i).classValue();
tempClassCounts[tempClass]++;
for (int j = 0; j < numConditions; j++) {
int tempValue = (int)dataset.instance(i).value(j);
conditionalCounts[tempClass][j][tempValue]++;
}//of for j
}//of for i
//Now for the real probability with Laplacian
for (int i = 0; i < numClasses; i++) {
for (int j = 0; j < numConditions; j++) {
int tempNumValues = (int)dataset.instance(i).attribute(j).numValues();
for (int k = 0; k < tempNumValues; k++) {
conditionalProbabilitiesLaplacian[i][j][k] = (conditionalCounts[i][j][k] + 1)/(tempClassCounts[i] + tempNumValues);
}//of for k
}//of for j
}//of for i
System.out.println("Conditional probabilities: " + Arrays.deepToString(conditionalCounts));
}//of calculateConditionalProbabilities
/**
* ***********************************************
* Calculate the Gaussian parameters.
* ***********************************************
*/
public void caculateGaussianParameters() {
gaussianparamters = new Gaussianparamters[numClasses][numConditions];
double[] tempValuesArray = new double[numInstances];
int tempNumValues = 0;
double tempSum = 0;
for (int i = 0; i < numClasses; i++) {
for (int j = 0; j < numConditions; j++) {
tempSum = 0;
//Obtain values for this class.
tempNumValues = 0;
//属于i类别的才继续,然后计数,否则跳过。
for (int k = 0; k < numInstances; k++) {
if ((int)dataset.instance(k).classValue() != i) {
continue;
}//of if
tempValuesArray[tempNumValues] = dataset.instance(k).value(j); //存储的是每个属于当前类的实例的当前属性值
tempSum += tempValuesArray[tempNumValues]; //当前类的当前属性总和
tempNumValues++; //属于i类别的实例总数
}//of for k
//Obtain parameters.
double tempMu = tempSum / tempNumValues; //获得均值
double tempSigma = 0;
//每个实例相当于一个自变量,就是密度函数中的X。
//for循环完成方差的计算
for (int k = 0; k < tempNumValues; k++) {
tempSigma += (tempValuesArray[k] - tempMu) * (tempValuesArray[k] - tempMu);
}//of for k
tempSigma /= tempNumValues;
tempSigma = Math.sqrt(tempSigma);
gaussianparamters[i][j] = new Gaussianparamters(tempMu, tempSigma);
}//of for j
}//of for i
System.out.println("gaussianparamters:" + Arrays.deepToString(gaussianparamters));
}//of caculateGaussianParameters
/**
* *******************************************************
* Classify all instances, the results are stored in predicts[].
* *******************************************************
*/
public void classify() {
predicts = new int[numInstances];
for (int i = 0; i < numInstances; i++) {
predicts[i] = classifyofDataTypeChose(dataset.instance(i));
}//of for i
}//of classify
/**
* *******************************************************
* Classify an instances according to the data type.
* @param paraInstance
* @return
* *******************************************************
*/
public int classifyofDataTypeChose(Instance paraInstance) {
if (dataType == NOMINAL) {
return classifyNominal(paraInstance);
}else if(dataType == NUMERICAL){
return 0;
}//of if
return -1;
}//of classifyofdataType
/**
* ********************************************************
* Classify an instances with nominal data.
* @param paraInstance
* @return BestIndex.
* ********************************************************
*/
public int classifyNominal(Instance paraInstance) {
// Find the biggest one.
double tempBiggest = -10000;
int resultBestIndex = 0;
for (int i = 0; i < numClasses; i++) {
double tempPseudoProbability = Math.log(classDistributionLaplacian[i]);
for (int j = 0; j < numConditions; j++) {
int tempAttributeValue = (int)paraInstance.value(j);
tempPseudoProbability += Math.log(conditionalProbabilitiesLaplacian[i][j][tempAttributeValue]);
}//of for j
if (tempBiggest < tempPseudoProbability) {
tempBiggest = tempPseudoProbability;
resultBestIndex = i;
}//of if
}//of for i
return resultBestIndex;
}//of classifyNominal
/**
* ******************************************************
* Classify an instances with Numerical data.
* @param paraInstance
* @return BestIndex
* ******************************************************
*/
public int classifyNumerical(Instance paraInstance) {
// Find the biggest one.
double tempBiggest = -10000;
int resultBestIndex = 0;
for (int i = 0; i < numClasses; i++) {
double tempPseudoProbability = Math.log(classDistributionLaplacian[i]);
for (int j = 0; j < numConditions; j++) {
double tempAttributeValue = paraInstance.value(j);
double tempSigma = gaussianparamters[i][j].sigma;
double tempMu = gaussianparamters[i][j].mu;
tempPseudoProbability += -Math.log(tempSigma)
- (tempAttributeValue - tempMu) * (tempAttributeValue - tempMu) / (2 * tempSigma * tempSigma);
}//of for j
if (tempBiggest < tempPseudoProbability) {
tempBiggest = tempPseudoProbability;
resultBestIndex = i;
}//of if
}//of for i
return resultBestIndex;
}//of classifyNumerical
/**
* *****************************************
* Compute accuracy.
* @return accuracy
* *****************************************
*/
public double computeAccuracy() {
double tempCorrect = 0;
double resultAccuracy = 0;
for (int i = 0; i < numInstances; i++) {
if (predicts[i] == (int)dataset.instance(i).classValue()) {
tempCorrect++;
}//of if
}//of for i
resultAccuracy = tempCorrect/numInstances;
return resultAccuracy;
}//of computeAccuracy
/**
* ******************************
* Test nominal data.
* ******************************
*/
public static void testNominal() {
System.out.println("Hello, Naive Bayes. I only want to test the nominal data.");
String tempFilename = "E:/Datasets/UCIdatasets/mushroom.arff";
NaiveBayes tempLearner = new NaiveBayes(tempFilename);
tempLearner.setDataType(NOMINAL);
tempLearner.calculateClassDistribution();
tempLearner.calculateConditionalProbabilities();
tempLearner.classify();
System.out.println("The accuracy is: " + tempLearner.computeAccuracy());
}//of testNominal
/**
* ******************************
* Test Numerical data.
* ******************************
*/
public static void testNumerical() {
System.out.println("Hello, Naive Bayes. I only want to test the numerical data.");
String tempFilename = "E:/Datasets/UCIdatasets/其他数据集/iris.arff";
NaiveBayes tempLearner = new NaiveBayes(tempFilename);
tempLearner.setDataType(NUMERICAL);
tempLearner.calculateClassDistribution();
tempLearner.caculateGaussianParameters();
tempLearner.classify();
System.out.println("The accuracy is: " + tempLearner.computeAccuracy());
}//of testNumerical
/**
* **************************************
* The entrance of the program.
* @param args
* **************************************
*/
public static void main(String args[]) {
testNominal();
testNumerical();
}//of main
}//of NaiveBayes
代码内容包含昨天的符号型数据,没有进行删除。数值型的处理方法和符号型的第一步是一致的,都是计算数据集中类的分布。数值型第二步是计算高斯分布的参数,即方差 和均值
。对应的方法是caculateGaussianParameters()。其余的计算精度,以及分类预测都大同小异。