【暑期每日一练】 day10

news2024/10/6 6:04:30

选择题

（1）

解析：

（2）

解析：

（3）

解析：

（4）

解析：

（5）

解析：

编程题

题一

描述

示例

解析：

代码实现

题二

描述

示例

提示

解析：

代码实现

总结

选择题

（1）

1、求函数返回值，传入 -1 ，则在64位机器上函数返回（）

int func(int x)
{
    int count = 0;
    while (x)
    {
        count++;
        x = x&(x - 1);//与运算
    } 
    return count;
}

A: 死循环 B: 64 C: 32 D: 16
答案：C

解析：

x=x&(x-1)这个表达式执行一次就会将x的2进制中最右边的1去掉，在x变成0之前，表达式能执行几次，就去掉几个1，所以这个代码实现了求一个有符号整数二进制补码中1的个数的功能，我们知道-1的补码是全1，而int类型4个字节32位，选C

（2）

2、读代码选结果（）

int count = 0;
int x = -1;
while(x)
{
    count++;
    x = x >> 1;
}
printf("%d",count);

A: 1 B: 2 C: 32 D: 死循环，没结果
答案：D

解析：

此题一个关键，有符号数右移运算高位是补符号位的，负数的符号位是1，所以x永远不会变为0，是个死循环

（3）

3、下述赋值语句错误的是（）

A: a = (b = (c = 2 , d = 3)) B: i++ C: a/b = 2 D: a = a < a + 1
答案：C

解析：

C选项中a/b是表达式，表达式计算的结果是一个值不能做左值

（4）

4、若有 int w=1, x=2, y=3, z=4; 则条件表达 w < x ? w : y < z ? y : z 的值是（）

A: 1 B: 2 C: 3 D: 4
答案：A

解析：

w<x?w:(y<z?y:z)加个括号应该就好理解了w<x为真，返回w，即表达式的值为1

（5）

5、以下程序运行后的输出结果是（）

int main()
{
    int a=1,b=2,m=0,n=0,k;
    k=(n=b<a)&&(m=a);
    printf("%d,%d\n",k,m);
    return 0;
}

A: 0,0 B: 0,1 C: 1,0 D: 1,1

答案：A

解析：

k=(n=b<a)&&(m=a);这部分的执行顺序如下：先执行n=b<a部分，其中，关系运算符优先级高于赋值运算符，所以先算b<a，得到0，n=0赋值运算的结果将作为括号内表达式的结果，即(n=b<a)&&(m=a)转换成(0)&&(m=a)，&&运算前表达式为假，则后面的括号(m=a)不运算，m值还是0，最后，&&的结果是0，即k=0

编程题

题一

描述

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

数据范围：两个数都满足 −10≤≤n≤1000

示例

解析：

十进制相加思想： 15+07 ，先计算不考虑进位的相加结果 12 （因为 5+7 的不考虑进位的结果是 2 ，遇 10 进位嘛），然后计算进位 5+7 进位是 10 ，则 10 与 12 再次相加，得到 22 ，进位为 0 ，则计算到此结束。

这里使用二进制求和完成，思想类似，但是二进制计算相加和进位不需要使用 + 符号

二进制相加思想：与十进制相同，先计算不考虑进位的相加结果（ 0+0 得 0 ， 1+1 进位得 0 ， 1+0 得 1 ），使用异或可以取得；然后计算相加的进位结果（同 1 的位置左移一位即可），使用相与后左移取得。

示例：

5 0101 + 7 0111
不考虑进位的相加结果 0101^0111 -> 0010
相加的进位 0101&0111 -> 0101 因为进位左移得到 1010
1010 + 0010
不考虑进位的相加结果 1010 ^ 0010 -> 1000
相加的进位 1010 & 0010 -> 0010 因为进位左移得到 0100
1000 + 0100
不考虑进位的相加结果 1000 ^ 0100 -> 1100
相加的进位 1000 & 0100 -> 0000 进位为0结束运算

代码实现

int Add(int num1, int num2 ) {
    while(num2 != 0)
    {    //进位不为0则持续与相加结果进行相加
        int tmp = num1 ^ num2;//得到每位相加不考虑进位的数据
        num2 = (num1 & num2) << 1;//同1的位相加则会进位
        num1 = tmp;
    } 
    return num1;
}

题二

描述

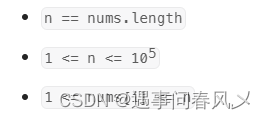
给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

示例

提示

解析：

numsSize 大小的数组，其中每个元素的数据在 [1, numsSize] 区间之内，解法其实并不复杂，以数组元素的绝对值作为下标，将对应位置的数据置为负数，比如 0 号位置是 3 ，则把 3 号位置的数据重置为负值，等到数组遍历重置完毕，只有缺失的这个数字对应的位置保留正数，其他出现过的数字位置都会是负数，要注意不要重复设置负数，因为负负得正。

示例

[2, 3, 3, 2, 4] 注意数组10个元素，值为[1-10]，但是访问下标应该在[0-9]之内,因此修改位置下标应该是值-1
0号元素是2，则将1号位置置为对应负值 [2, -3, 3, 2, 4]
1号元素是3，则将2号位置置为对应负值 [2, -3, -3, 2, 4]
2号元素是-3，绝对值为3，将2号位置为负值，但是2号位已经重置过，不需要重置，否则会变正数[2, -3, -3, 2, 4]
3号元素是-2，绝对值为2，将1号位置为负值，但是1号位已经重置过，不需要重置，否则会变正数[2, -3, -3, 2, 4]
4号元素是4，则将3号位置置为对应负值 [2, -3, -3, -2, 4]
遍历数组得到0,4两个位置的数据是大于0的，因为人家数值从1开始，因此+1后得到1， 5两个缺失的数字

代码实现

int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize)
{
  for (int i = 0; i < numsSize; i++)
  {
    if (nums[abs(nums[i]) - 1] > 0)
      nums[abs(nums[i]) - 1] = -(nums[abs(nums[i]) - 1]);
  }
  int *ret = (int *)malloc(sizeof(int) * (numsSize));
  *returnSize = 0;
  for (int i = 0; i < numsSize; i++) 
  {
    if (nums[i] > 0)
    {
      ret[*returnSize] = i + 1;
      *returnSize += 1;
    }
} 
  return ret;
}