目录
一、总述
1.1 前端思路
1.2 后端思路
二、前端实现
2.1 判断是否能进行拖拽
2.2 收集受影响的节点，提交给服务器
三、后端实现
四、总结
一、总述
这个拖拽功能对于这种树形的列表，整体的搬迁是很方便的。但是其实现却并不是那么的简单。
1.1 前端思路
花样主要体现在前端上面，前端有两个大的部分，一个是使用elementUI提供给我们的api判断是否能够进行拖拽，因为并不是能够随意的拖拽的，因为这个树形列表是三级分类，受到了三级的限制。另外一个部分就是拖拽之后，会有一些节点的信息将发生改变，需要进行收集，然后统一发到后端服务器，进行修改
1.2 后端思路
而后端的话没什么，就一个修改接口就行了。
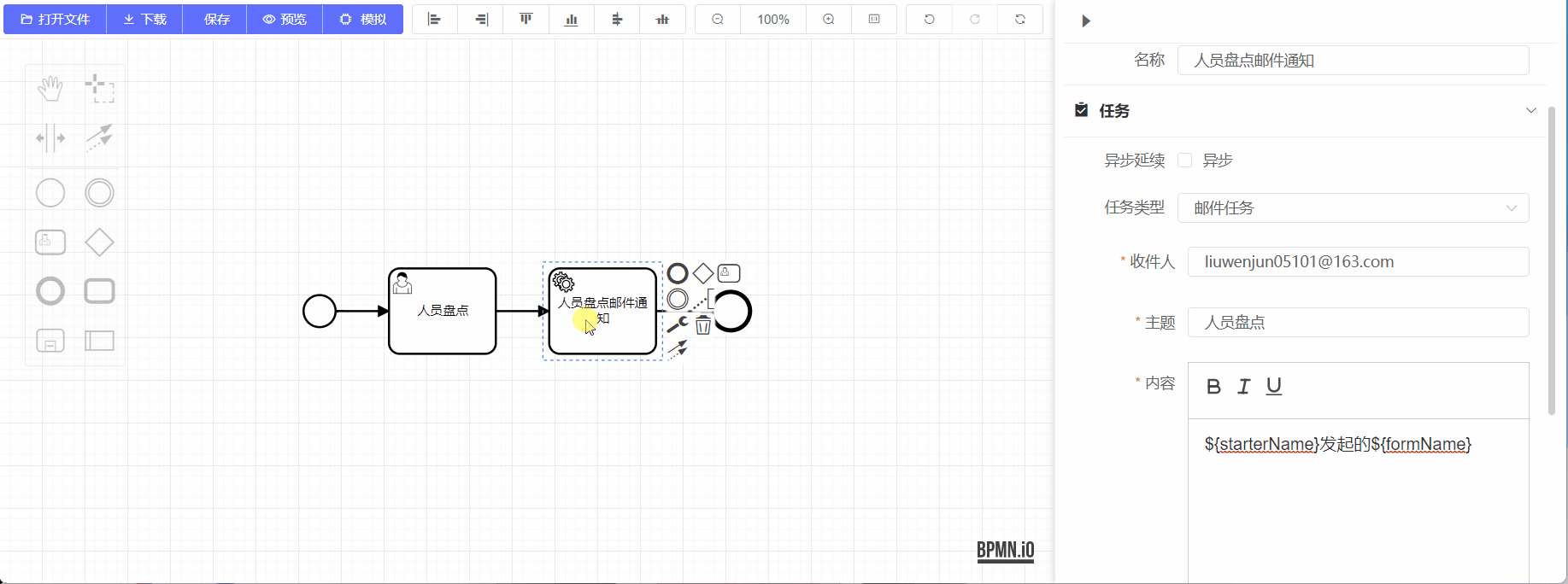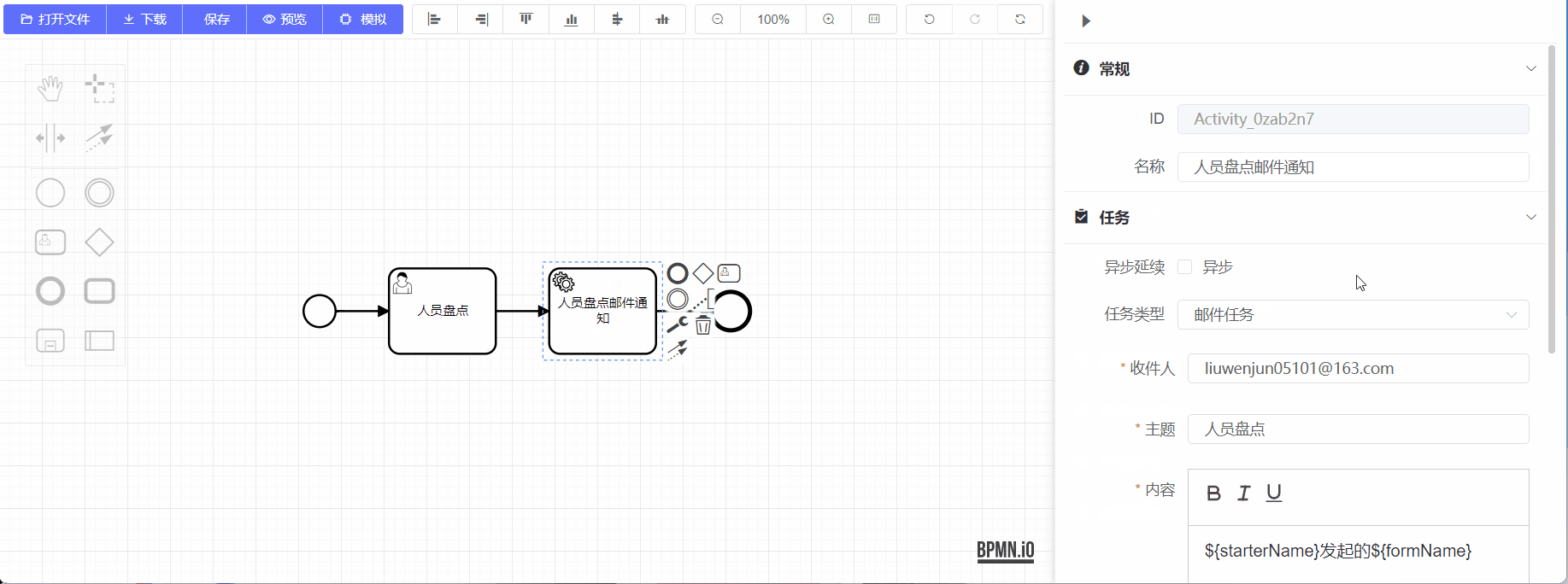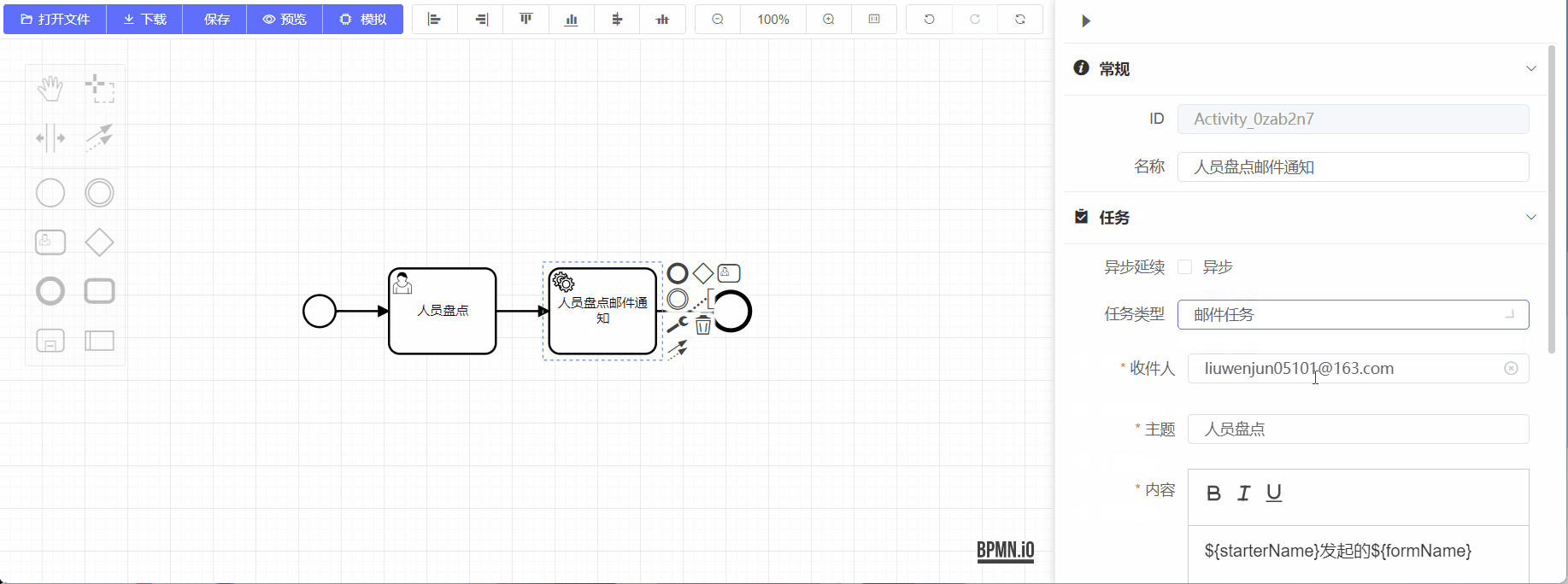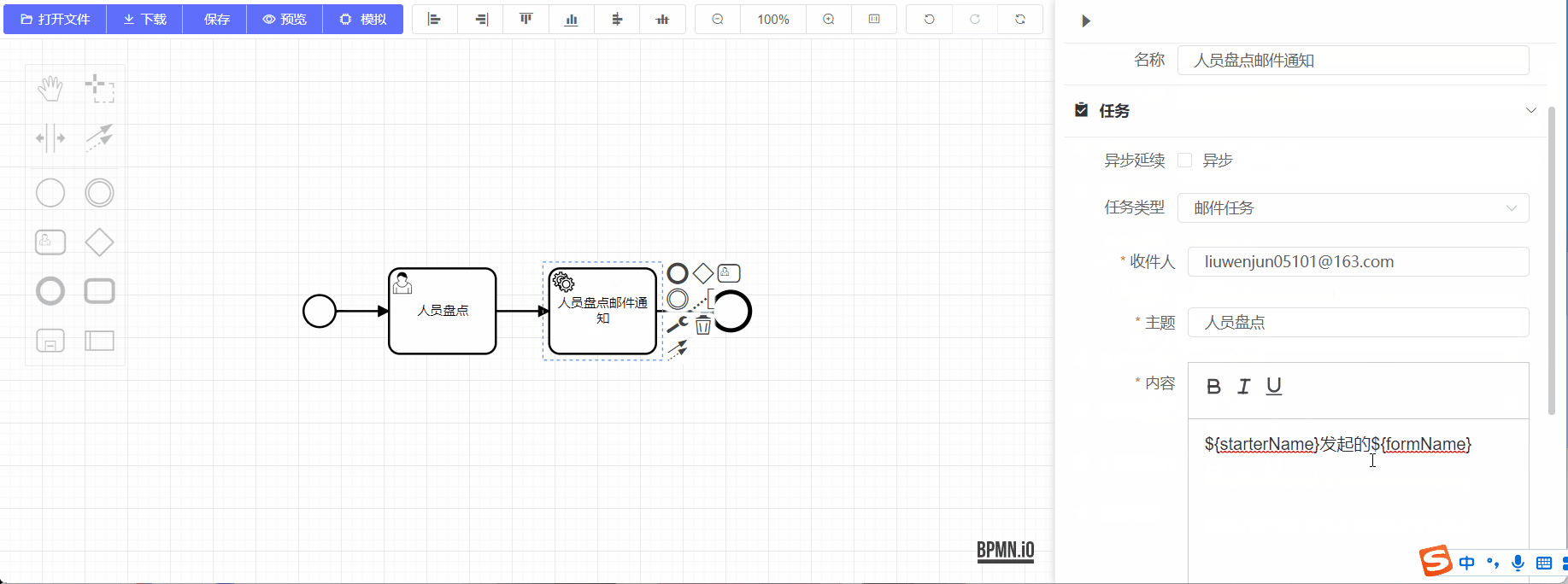
二、前端实现
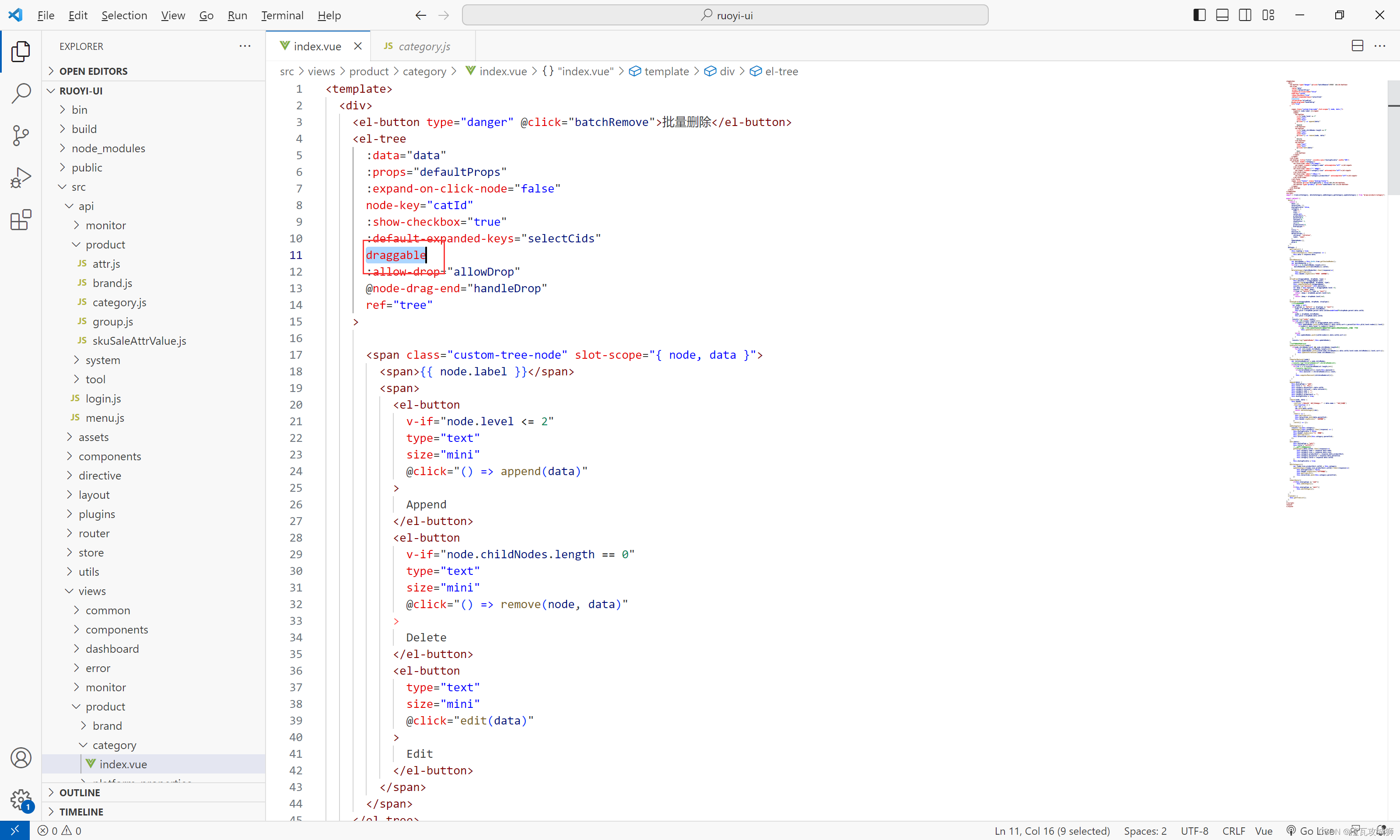
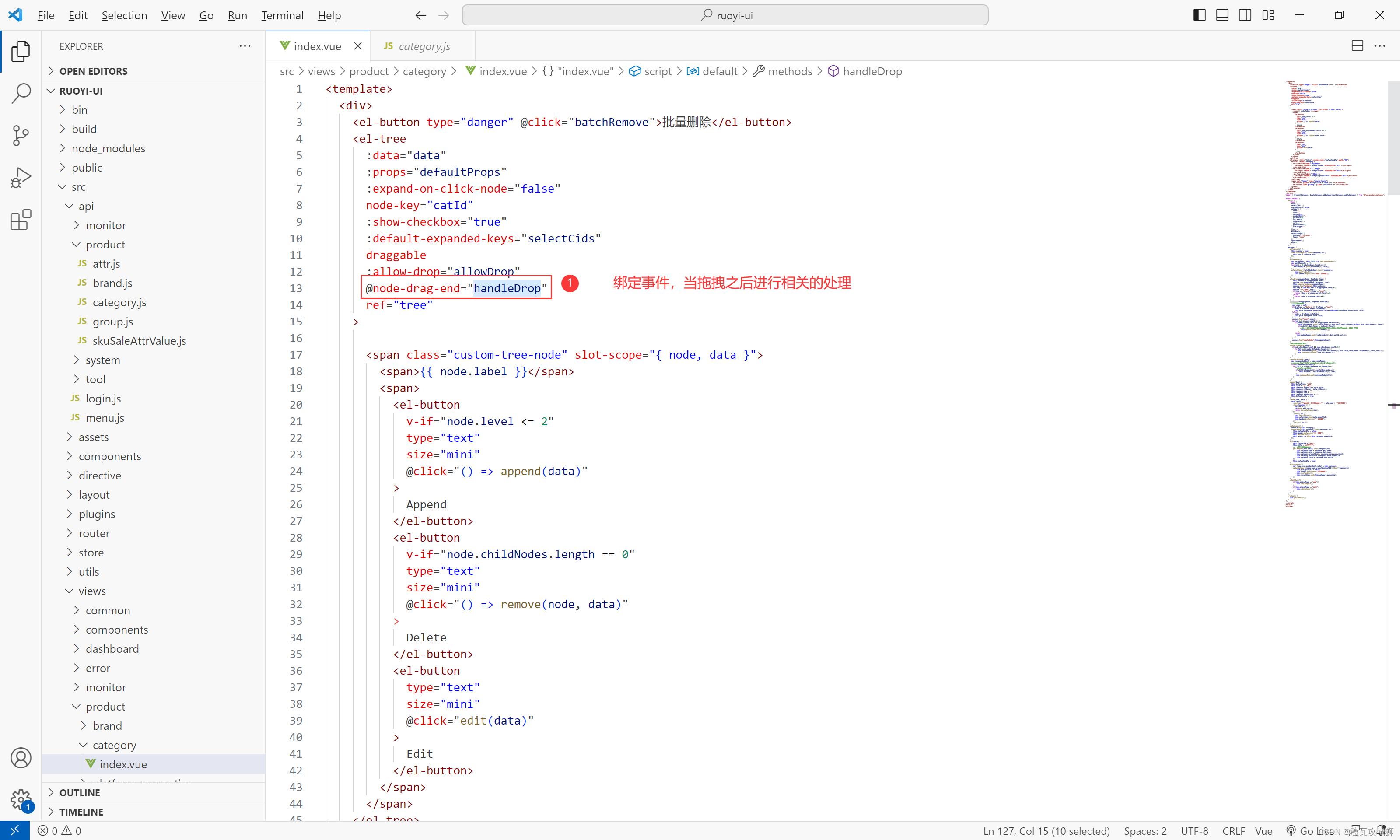
当然最开始肯定得开启树形控件的可拖拽功能
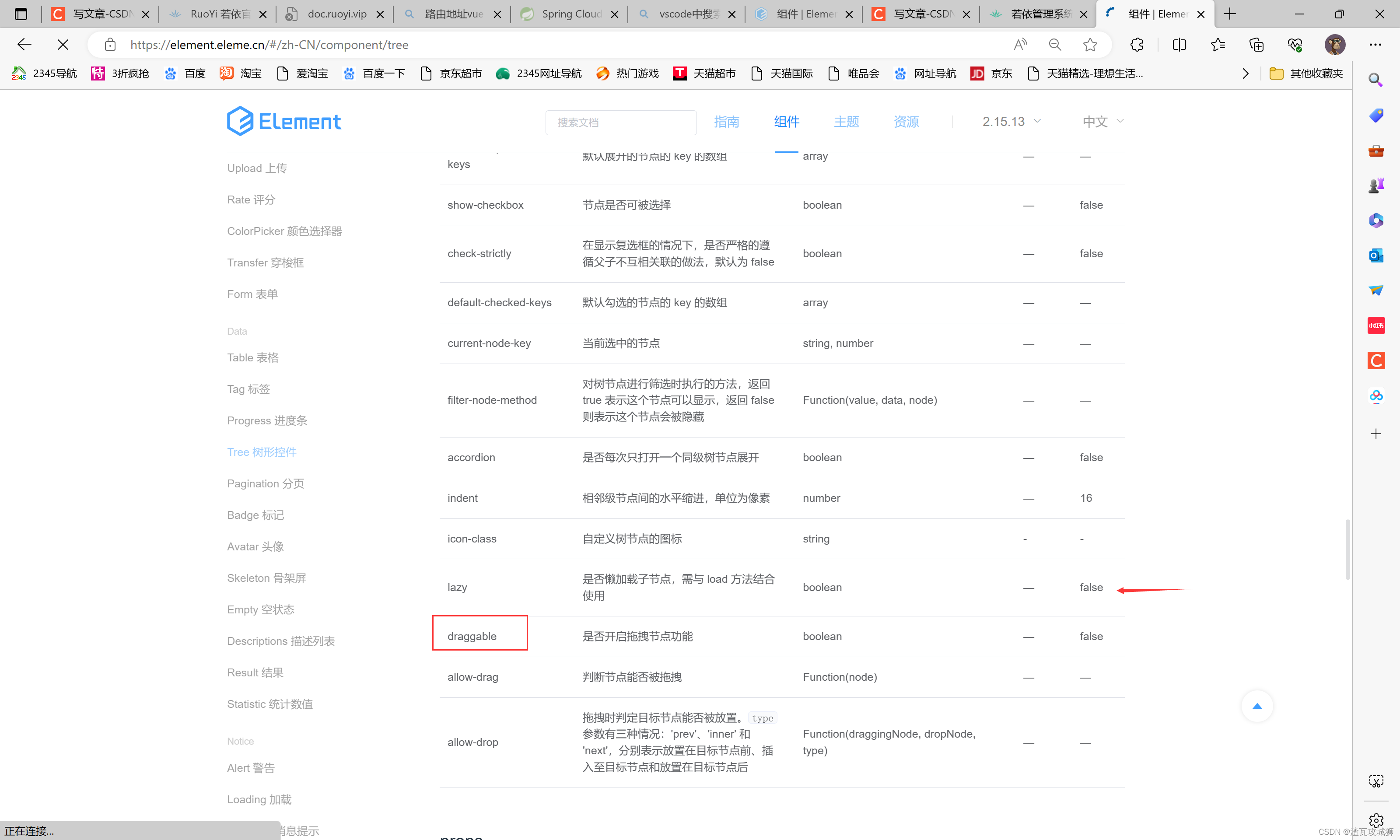
默认是未开启的，需要我们手动开启
2.1 判断是否能进行拖拽
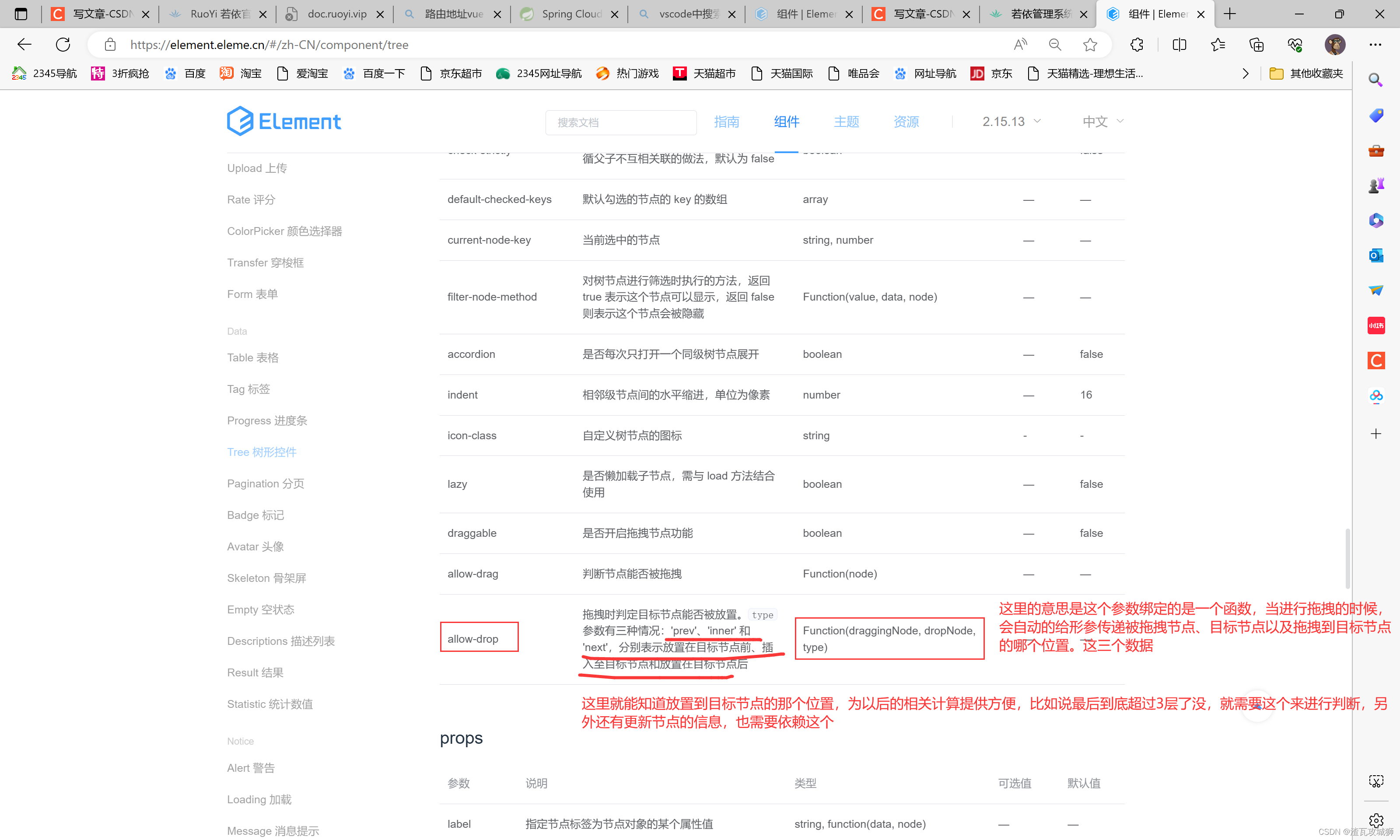
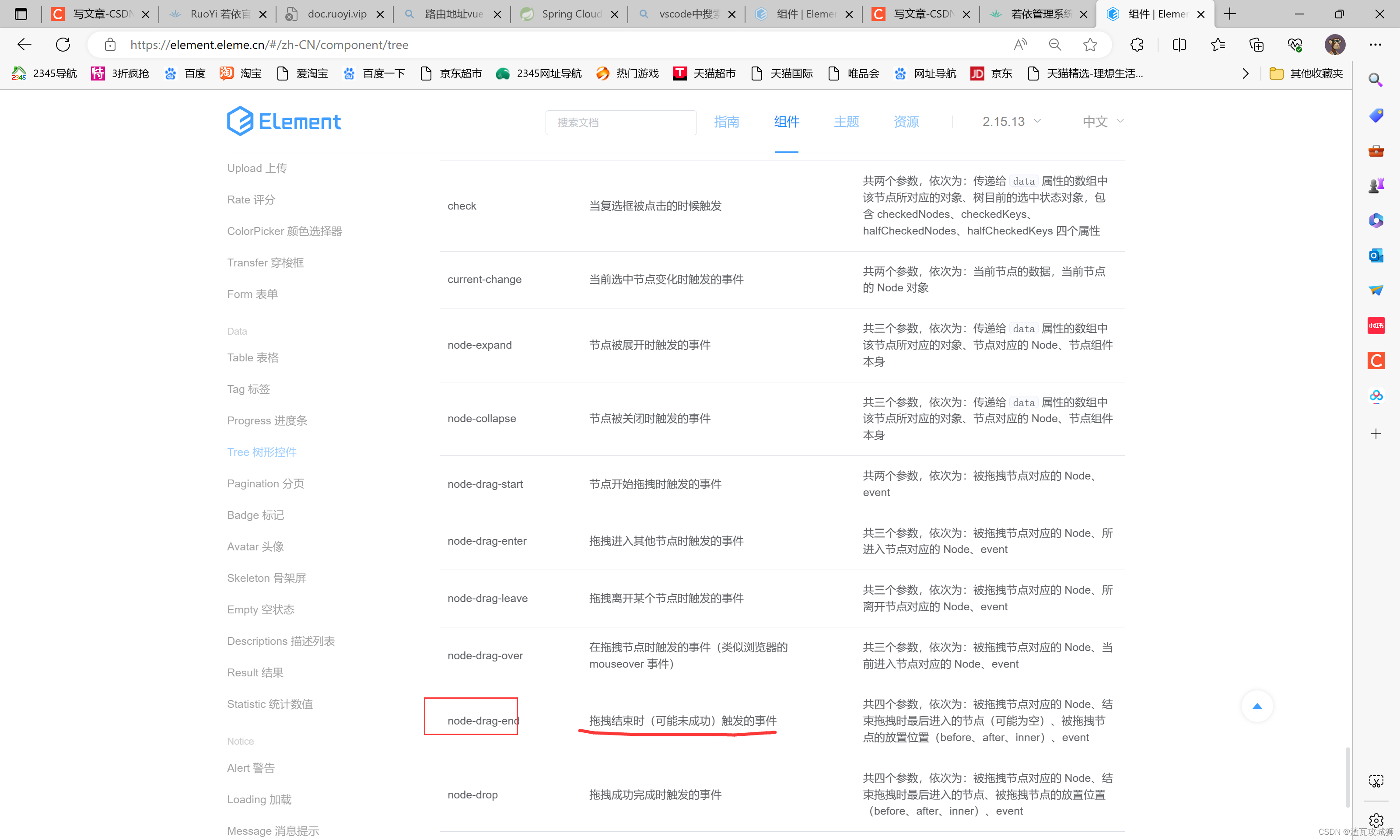
完成这个功能需要依靠elementUI提供给我们的api，我下面简单的介绍一下这个api
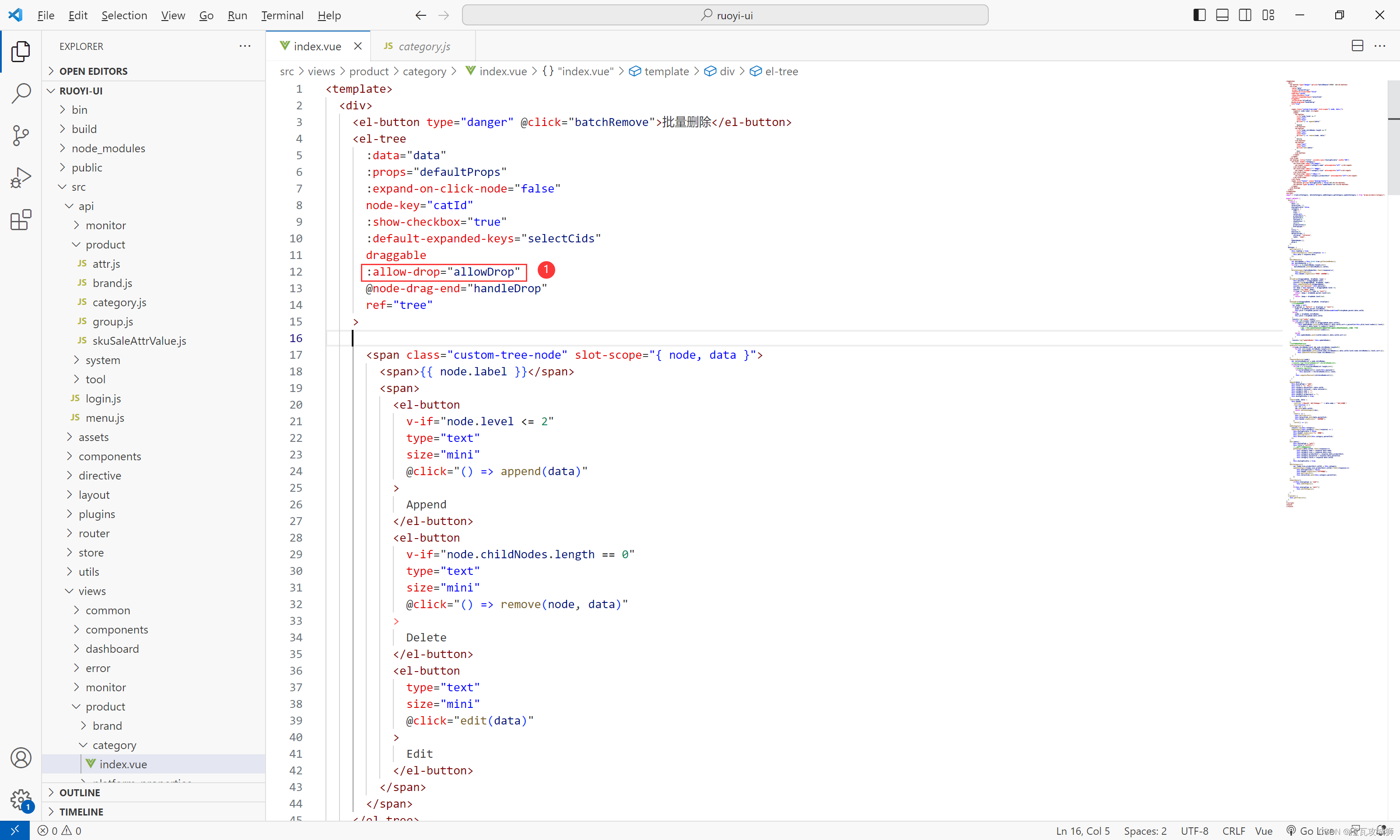
然后在树形控件的参数那里放上这个参数，并给上一个方法
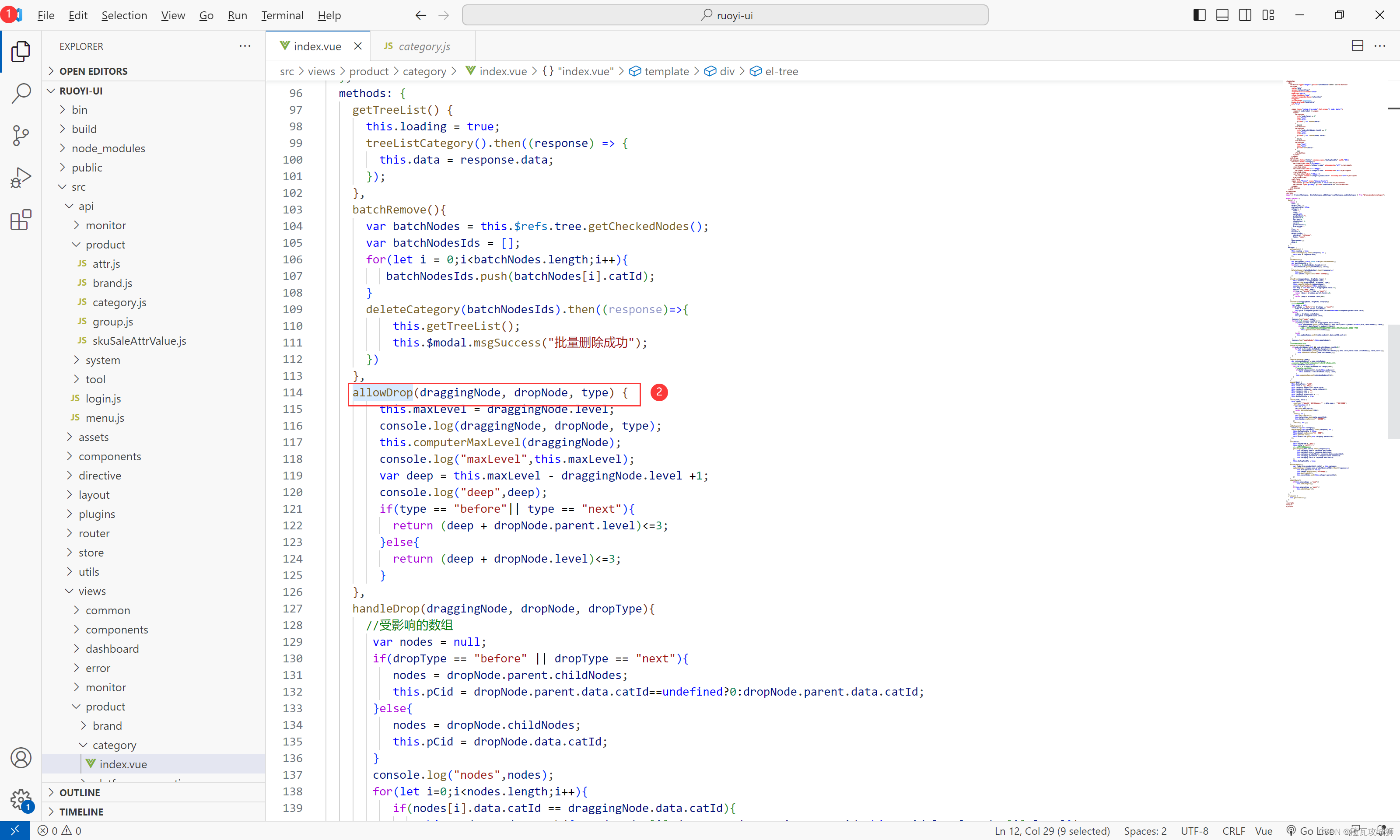然后根据它提供给我们的这三个信息来进行判断，最终决定是否能拖拽成功。
这个判断的核心逻辑是：
1. 先计算出被拖拽节点的最大层数
计算方法是：使用打擂台的方式计算出子节点的最大深度，并递归的计算其又子节点的最大深度，得到这个目标节点的子节点的最大深度，但这个只是子节点的最大深度，并不是以被拖拽节点为始发层的最大层数，那么如何计算呢？实际上就是求差，现在求得是总的，我们并不需要前面的那一截了，因为等下我要换地方了，前面的那一截就换了，而被拖拽的那一部分是不变的，那前面的那一部分又该怎样得到呢？
其实就是当前拖拽节点的层级，然后使用子节点的最大深度 - 当前拖拽节点的层数 + 1 就得到了当前被拖拽节点的最大层数。
1.1 使用打擂台的方式计算出子节点的最大深度
computerMaxLevel(node){
var childrenNodeList = node.childNodes;
//console.log("childrenNodeList",childrenNodeList);
if(childrenNodeList!=null){
for(let i = 0;i<childrenNodeList.length;i++){
//console.log(1111);
if(childrenNodeList[i].level>this.maxLevel){
this.maxLevel = childrenNodeList[i].level;
}
this.computerMaxLevel(childrenNodeList[i]);
}
}
}2. 计算拖拽后总层数（也就是目标结果）
现在的话拖的一部分已经有了，但是拖到的位置，那里所占据的层数还没有考虑，现在的工作就是加上新地方的层数。
现在的计算得按照不同情况进行计算，因为有两种情况：
2.1 与拖到的目标节点同层级，互为兄弟
那么就是目标节点的父节点的层级 + 刚刚求出的被拖拽节点的最大层数
2.2 是拖到的目标节点的孩子
那么直接就是目标节点的层级 + 刚刚求出的被拖拽节点的最大层数
3. 直接判断
当拖拽后的总层数<=3时，判断方法返回true，拖拽成功
否则拖拽失败
allowDrop(draggingNode, dropNode, type) {
this.maxLevel = draggingNode.level;
console.log(draggingNode, dropNode, type);
this.computerMaxLevel(draggingNode);
console.log("maxLevel",this.maxLevel);
var deep = this.maxLevel - draggingNode.level +1;
console.log("deep",deep);
if(type == "before"|| type == "next"){
return (deep + dropNode.parent.level)<=3;
}else{
return (deep + dropNode.level)<=3;
}
}2.2 收集受影响的节点，提交给服务器
首先要明白有哪些节点会受到影响。
1. 前序的数据域中数据的定义
一、考虑影响了别人
其实就是影响了兄弟。
如果说被拖拽节点与目标节点经拖拽后互为兄弟关系的话，那么就会影响到其他兄弟的排序顺序，因为现在多加了一个节点，势必这个新增节点之后的节点顺序都要向后推一位。（这些兄弟就需要收集起来）
当然如果被拖拽节点与目标节点经拖拽后互为父子关系的话，那么就改变了目标节点的子节点的那些兄弟。
二、考虑影响了自己
被拖拽节点拖拽后，到其他父节点上面去了，因此被拖拽节点的父节点也发生了改变，另外被拖拽节点的层级也将发生变化，其被拖拽节点的子节点的父节点不会变，还是被拖拽节点，可是其子节点的层级肯定发生了改变，其子节点的字节点的层级也发生了改变，因此需要递归操作
总的来说标红的三处地方就是需要提交到服务器的节点，但是并不是需要提供节点的完整信息，而是提供需要修改的信息即可：
1. 对于那些兄弟节点，提供兄弟节点的 id和 排序值就可以了，根据id主键进行修改
2. 对于那个被拖拽节点，需要提供被拖拽节点的 id、父节点、还有最新的层级
3. 对于其被拖拽节点的字节点，需要提供其节点的id 以及节点最新的层级即可
最后将这三部分的节点，提交给服务器就行了。
思路我说了，最后代码进一步的简洁，我已经说的很明白了，在截图中，这里为什么和我刚刚说了有点不一样，就是那个sort字段为什么任何时候都需要加上这个，是因为其实数据库本来全是0的，正是靠这个算法才赋上值，当然这里也不全面，只涉及到修改了的部分，详细的代码参考如下：
handleDrop(draggingNode, dropNode, dropType){
//受影响的数组
var nodes = null;
if(dropType == "before" || dropType == "next"){
nodes = dropNode.parent.childNodes;
this.pCid = dropNode.parent.data.catId==undefined?0:dropNode.parent.data.catId;
}else{
nodes = dropNode.childNodes;
this.pCid = dropNode.data.catId;
}
console.log("nodes",nodes);
for(let i=0;i<nodes.length;i++){
if(nodes[i].data.catId == draggingNode.data.catId){
this.updateNodes.push({catId:nodes[i].data.catId,sort:i,parentCid:this.pCid,level:nodes[i].level})
if(nodes[i].data.level != nodes[i].level){
//因为被拖拽的节点的层级发生了改变，因此其子节点的层级也会跟着改变
this.updateChirenLevel(nodes[i]);
}
}else{
this.updateNodes.push({catId:nodes[i].data.catId,sort:i})
}
}
console.log("updateNodes",this.updateNodes);
},
//修改子节点的level
updateChirenLevel(node){
if(node.childNodes!=null && node.childNodes.length>0){
for(let i=0;i<node.childNodes.length;i++){
this.updateNodes.push({catId:node.childNodes[i].data.catId,level:node.childNodes[i].level,sort:i});
this.updateChirenLevel(node.childNodes[i]);
}
}
},最终将需要更新的节点数组作为请求参数提交给后端，在后端修改即可
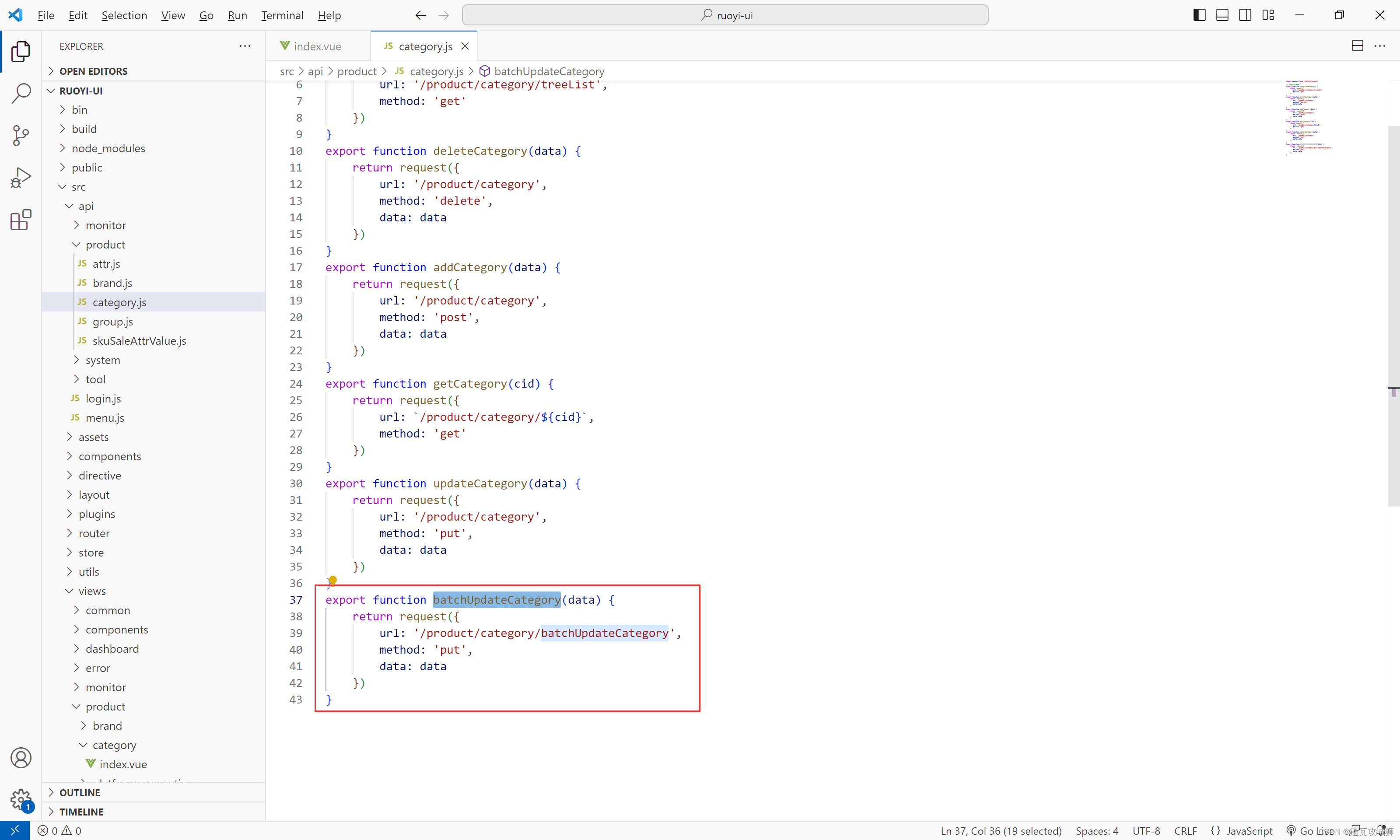
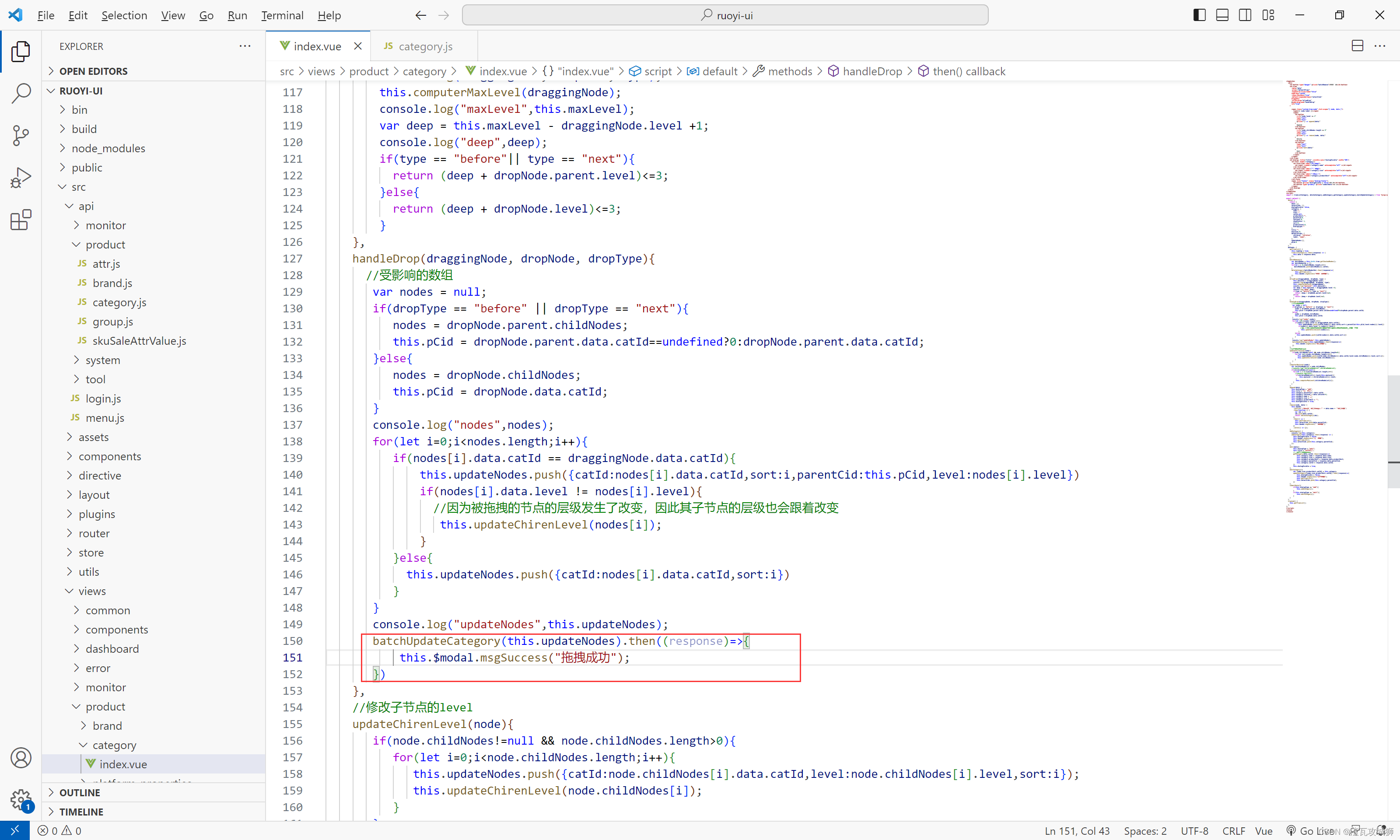
三、后端实现
后端的话很简单，就一个修改接口，使用MP的方法，根据主键进行批量修改。
/**
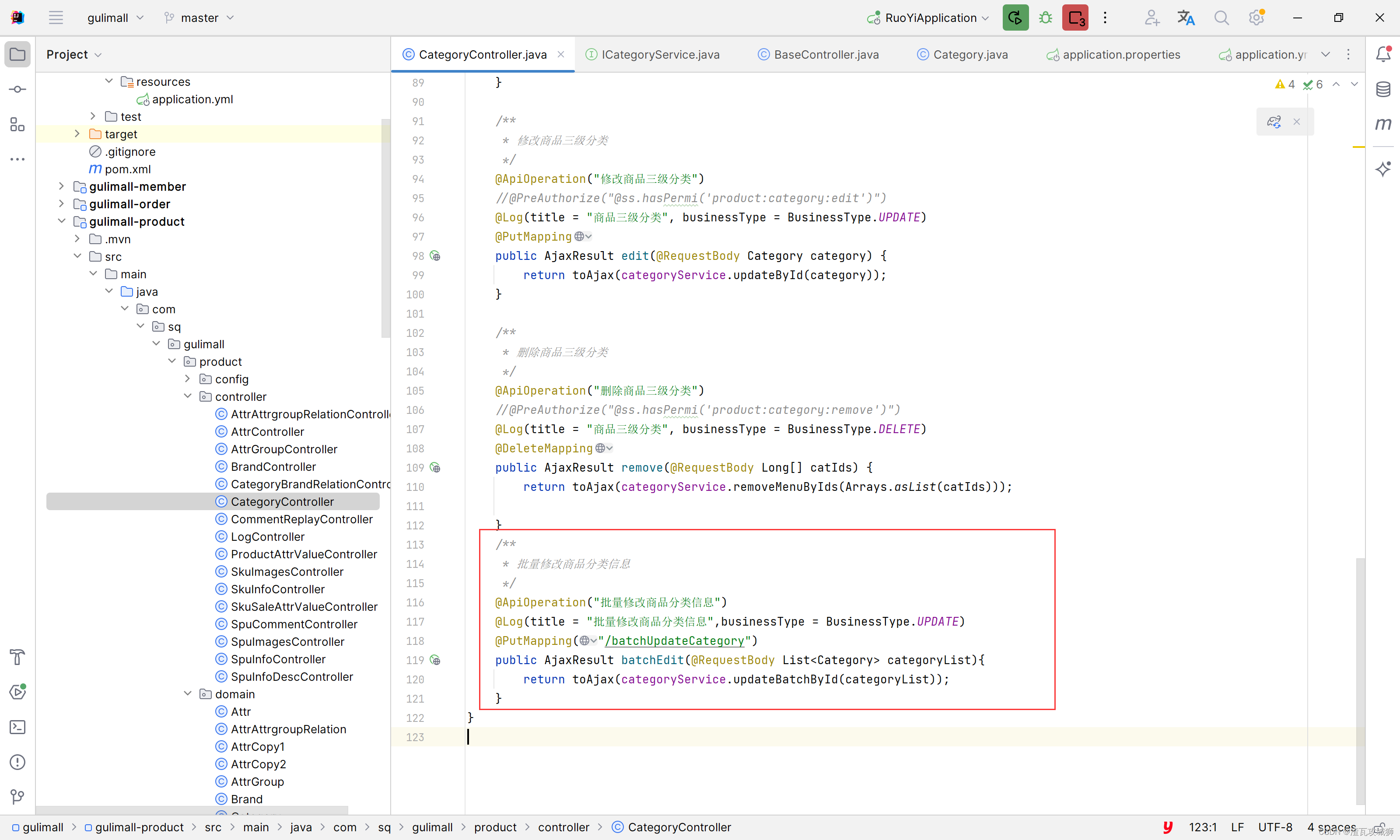
* 批量修改商品分类信息
*/
@ApiOperation("批量修改商品分类信息")
@Log(title = "批量修改商品分类信息",businessType = BusinessType.UPDATE)
@PutMapping("/batchUpdateCategory")
public AjaxResult batchEdit(@RequestBody List<Category> categoryList){
return toAjax(categoryService.updateBatchById(categoryList));
}四、总结
其实总的来说只要想清楚了，其实还是很简单的。
这里关键是前端的逻辑稍微有那么点复杂，有写算法题的那味了，但是仔细一想还是挺简单的。
主要是关系，还有数量关系等，比如说求被拖拽节点的最大层数，需要用到数量计算表达式
其实就是一个减法，用子节点的最大深度减去被拖拽节点的层数 + 1 即可求得其被拖拽节点的最大层数，有了这个最大层数然后再配合目标那里的层数，按照不同的条件进行相加，最后总的层数不就出来了吗？有了总层数当然是否能拖拽就好判断了。
另外还有就是搬过来之后会导致一些节点的信息发送改变，此时就需要收集起来，发给后端，再后端进行修改，这里关键是想明白到底哪些节点修改了，需要收集哪些属性，其实也是很简单的，想清楚就好了。
