先回顾下微分的概念，首先我们找到一个道路x，它是关于时间t的函数，然后我们可以得到一个速度，也就是切向量，所有道路的切向量组成了切空间。如果从泛函角度来理解，它应该是一个求偏导的基。是一个向量。而微分，则是在固定函数f，注意f是作用在道路x上的。对于固定的f(x),我们通过让每个偏导都求一遍，然后求和就得到了最终的微分公式。而微分是切空间的对偶空间，它的基是dx,注意dx1(x)是取x的第一个坐标，所以对于切向量，那么dx1就是取它的第一个坐标。然后我们让他作用于一个基，那么dx1(第一个基）肯定=1，其他是0，刚好复合对偶空间的定义。终于明白了基为什么dx.

其次，为什么微分形式dx1^dx2....dx^n这么重要呢？

因为dx意味着取坐标，取坐标操作对应的行列式的运算是斜对称的形式。是有良好性质的。

而且，任何一个k形式都可以看成F作用在基上乘以一组取坐标的外积。

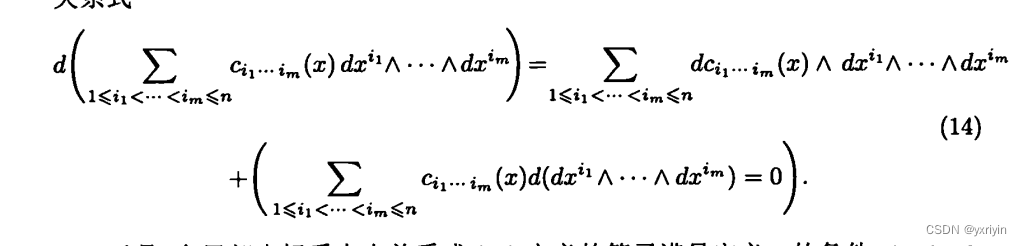
公式14中的元素是流形M上的m次微分形式在某一张图下面的坐标形式。

 

因为m次微分形式就是m形式，必然可以变成上面的坐标形式的。

后面内容有点复杂，我们先回到之前的学习内容：

k形式其实可以看成k个1形式的乘积，我们要引入斜对称的k形式，就需要增加一个运算A，而A的运算本质是通过行列式的组织，而这个和外积的运算刚好对应，所以外积可以看成A的一种。那么我们把k个外积相乘，可以看成k形式加斜对称。

从另一个角度说，我们认为k形式可以这么表示：

 

如果L是个斜对称形式，那么可以进一步简化：

 

从这个过程，我们也能看到为什么斜对称的k形式可以变成一堆外积来表示。

 这一段现在仔细看有不同的体会，首先我们知道微分k形式它是一个斜对称的k形式，所以能分解成坐标形式。所以，我们知道了，所有微分k形式，都可以用最简的坐标的微分1形式外积而成，他们的线性组合。

 这一段也终于看明白了，微分1形式，功形式，在笛卡尔坐标系下，ai(x)就是Fi本身，因为那是标准正交基。df方向导数也可以看成梯度的微分1形式。

这里是外微分的定义，应该是后面为了多元微积分一起弄的铺垫吧。

 

d(dx1)=0 

 梯度表示怎么流的最快，外微分一次，就变成了怎么旋转的最快，而散度就是说发散的快还是聚拢的快。

这里是后拉算子，其实就是对偶空间下的算子。对于U->V的映射，可以变成V->U的反向映射，而且满足一定的数量关系。对于微分p形式，额对应了这样的后拉算子。

 

 这是线性和复合函数求导法则的结果。

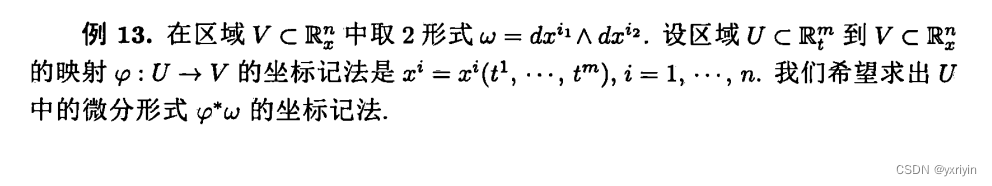 这是最重要的一道题了。坐标记法，坐标形式，就是我们把具体的向量用坐标和基的组合表示出来。然后抽取出映射的重叠部分即可。比如w，它的坐标记法我们前面说了：

 现在我们就把对应的映射变换会导致坐标形式上的变换想一下：

其实就是换元法。本来是x1,x2为未知数，现在知道x=x(t)，要换成t作为未知数。因为我们需要的是dx1,dx2并不是直接的x，所以他是V上的微分形式，所以我们要看用拉回，能把微分形式变成什么。

首先微分形式是作用在切空间的，所以我们取的也是切空间。这里取的是两个向量，因为最终只是二维曲面的相互转化。然后根据映射的导数，可以得到对应V中的切向量。因为我们要知道的坐标表示，肯定要写出坐标的形式。

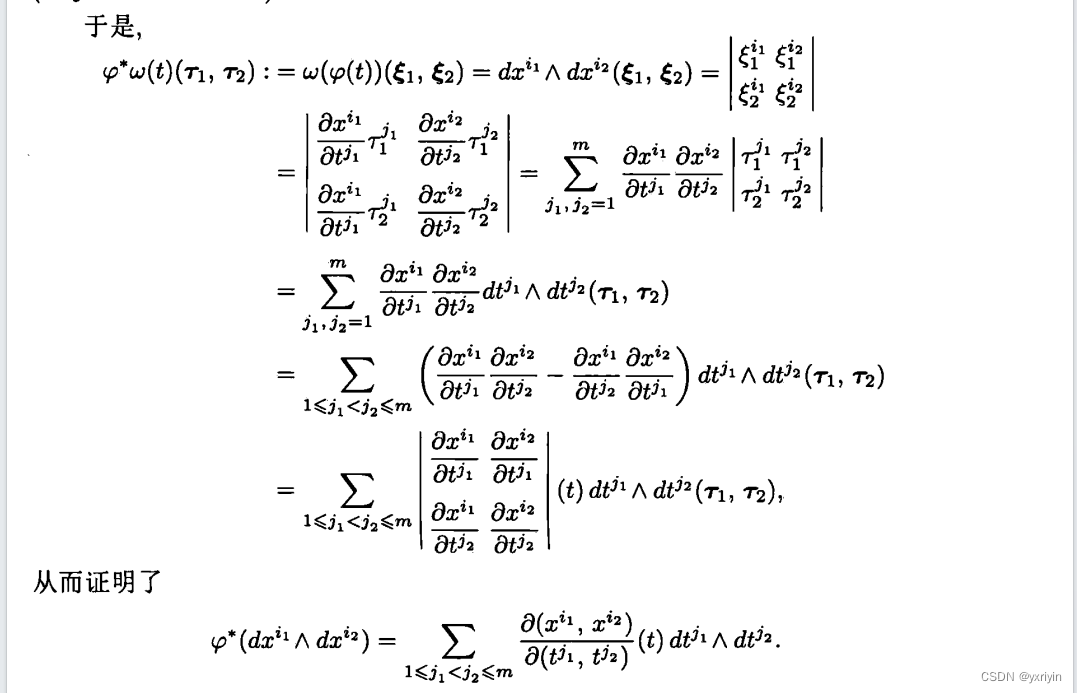
后面都是计算了。

 

证明d(df)=0:

 

 终于看完了初步形式，继续流形上的积分

 这里理解下就好了，对于图册没有重复覆盖的点，那么函数集合就是一个，里面就是1，对于重复覆盖的点，比如有两个图册覆盖了，那么每个分0.5就行了。