1. bitset 优化背包
https://loj.ac/p/515
题意:
给 n 个 <= n 的数,每个数有取值范围 a[ i ] - b[ i ],令 x 为 n 个数的平方和,求能构成的 x 的个数
样例:
5
1 2
2 3
3 4
4 5
5 6
26
思路:
背包dp,dp[ i ][ j ] 表示用前 i 个数能不能组成 j ,用 bitset 优化
用一个 bitset dp 维护 当前的数 可以组成哪几个 x ,用 bitset tmp 维护 当前的状态 可以转移到哪几个状态,滚动优化空间,复杂度为O(n^5 / 64)
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+5;
bitset<N>dp,tmp;
void solve(){
int n;
cin>>n;
dp.set(0); //初始化
for(int i=1;i<=n;i++){
int a,b;
cin>>a>>b;
tmp.reset();
for(int j=a;j<=b;j++){
tmp|=(dp<<(j*j));
}
dp=tmp;
}
cout<<dp.count()<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T=1;
//cin>>T;
while(T--){
solve();
}
return 0;
}2. bitset 优化图上问题(可达性统计问题)
https://www.acwing.com/problem/content/166/
题意:
给一个 n 个点,m 条边的 有向无环图,求每个点能到达的 点的个数
样例:
10 10
3 8
2 3
2 5
5 9
5 9
2 3
3 9
4 8
2 10
4 9
1
6
3
3
2
1
1
1
1
1
思路:
反向建图,然后利用 拓扑排序,进行图上dp,dp[ i ][ j ]表示从点 i 出发能不能到达 点 j ,用 bitset优化,若存在 u - > v 的边,则 dp[ u ] | = dp[ v ]
复杂度为 O(n^2 / 64)
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3e4+5;
int head[N],cntt=0;
struct Edge{
int to,next,val;
}edge[N];
void add(int u,int v,int x){
edge[++cntt].to=v;
edge[cntt].val=x;
edge[cntt].next=head[u];
head[u]=cntt;
}
int deg[N];
bitset<N>dp[N];
void solve(){
int n,m;
cin>>n>>m;
while(m--){
int u,v;
cin>>u>>v;
add(v,u,1);
deg[u]++;
}
queue<int>q;
for(int i=1;i<=n;i++){
dp[i][i]=1;
if(deg[i]==0)q.push(i);
}
while(!q.empty()){
int tmp=q.front();
q.pop();
for(int i=head[tmp];i;i=edge[i].next){
int y=edge[i].to;
dp[y]|=dp[tmp];
deg[y]--;
if(deg[y]==0)q.push(y);
}
}
for(int i=1;i<=n;i++)cout<<dp[i].count()<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T=1;
//cin>>T;
while(T--){
solve();
}
return 0;
}
3. bitset 优化枚举
https://codeforces.com/contest/333/problem/E
题意:
给 n 个点,找 3 个点,以这三个点为圆心,画 3 个半径相同互不相交的圆,求最大的半径
可以转化为,给 n 个点,找出 最小边最大 的三角形,求最大的最小边
思路:
将所有边按边长降序排列,依次枚举当前边作为最小边,然后枚举其它点,若存在某点 和 当前的边的两个点都已经连有边(即存在以当前边为最小边的三角形),则找到答案,否则连上这条边
直接枚举的复杂度是 O ( n^3 ) ,可以用一个标记数组 vis [ i ] [ j ] 表示有没有 i - j 的边,用 bitset 优化这个数组,每次 对于 x-y 的边,通过 vis[x] & vis[y] 可以在 O ( n/64 ) 时间内快速判断有没有符合条件的点,在 O ( n^3/64 ) 复杂度下通过本题
样例:
7 2 -3 -2 -3 3 0 -3 -1 1 -2 2 -2 -1 0
1.58113883008418980000
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=3e3+5;
double x[N],y[N];
double length(int a,int b){
return sqrt((x[a]-x[b])*(x[a]-x[b])+(y[a]-y[b])*(y[a]-y[b]));
}
struct node{
int x,y;
double len;
bool operator<(const node a)const{
return len>a.len;
}
};
vector<node>edge;
bitset<N>vis[N];
void solve(){
int n;
cin>>n;
for(int i=1;i<=n;i++)cin>>x[i]>>y[i];
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
edge.push_back((node){i,j,length(i,j)});
}
}
sort(edge.begin(),edge.end());
for(auto e:edge){
int x=e.x,y=e.y;
double len=e.len;
if((vis[x]&vis[y]).any()){
cout<<fixed<<setprecision(8)<<len/2<<endl;
return;
}
vis[x].set(y);
vis[y].set(x);
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T=1;
//cin>>T;
while(T--){
solve();
}
return 0;
}
4. bitset 优化 01 矩阵乘法
http://acm.hdu.edu.cn/showproblem.php?pid=7293
题意:
给一张无向图,求图中有多少个 下图形状的子图
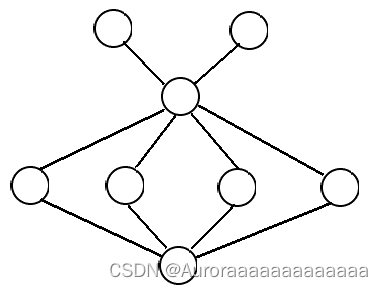
思路:
对无向图建邻接矩阵,对邻接矩阵进行平方,新矩阵 a[ i ] [ j ] 表示 从 i 点到 j 点 长为2的路径个数,枚举子图中 度为6和4的两个点,通过组合数计算子图数量即可,复杂度为 O(n^3)
利用 bitset 优化,01矩阵的平方 可以通过 b [ i ] [ j ] = ( r [ i ] & c [ j ] ) . count () 计算,由于无向图的邻接矩阵是 对称矩阵,所以直接用 ( vis [ i ] & vis [ j ] ) . count () 表示矩阵平方,复杂度为 O(n^3/64)
样例:
1
8 10
1 2
1 3
1 4
1 5
1 6
1 7
8 4
8 5
8 6
8 7
1
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){ //快读快写
int x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x;
}
inline void write(int x){
if(x>9)write(x/10);
putchar(x%10+'0');
}
const int N=1005;
const int mod=1e9+7;
int fact[N],inv[N]; //O(1)求组合数
inline int qpow(int a,int b){
int ans=1;
while(b>0){
if(b&1)
ans=(ans*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return ans;
}
void Cinit(){
fact[0]=1,inv[0]=1;
for(int i=1;i<=N-1;i++){
fact[i]=fact[i-1]*i%mod;
}
inv[N-1]=qpow(fact[N-1],mod-2)%mod;
for(int i=N-2;i>=1;i--){
inv[i]=inv[i+1]*(i+1)%mod;
}
}
inline int C(int a,int b){
if(a<0||b<0||a<b)return 0;
return fact[a]*inv[a-b]%mod*inv[b]%mod;
}
bitset<N>vis[N];
void solve(){
int n=read(),m=read();
for(int i=1;i<=n;i++)vis[i].reset();
while(m--){
int u=read(),v=read();
vis[u].set(v);
vis[v].set(u);
}
int ans=0;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
int cnt1=vis[i].count(),cnt2=vis[j].count();
int cnt=(vis[i]&vis[j]).count(); // 矩阵乘
if(vis[i][j]){ //不能选两点直接相连的边
cnt1--,cnt2--;
}
ans+=C(cnt1-4,2)*C(cnt,4);
ans%=mod;
ans+=C(cnt2-4,2)*C(cnt,4);
ans%=mod;
}
}
write(ans);
putchar('\n');
return;
}
signed main(){
Cinit();
int T=read();
while(T--){
solve();
}
return 0;
}
5. bitset 优化 floyd
https://www.luogu.com.cn/problem/P4306
题意:
给一张有向图,求每个点能到达的点的个数的和
样例:
3 010 001 100
9
思路:
考虑 floyd 上 dp,dp [ i ] [ j ] 表示点 i 能到达点 j ,转移方程为 dp[ i ][ j ] |= (dp[ i ][ k ] &dp[ k ][ j ] )
用 bitset 优化转移,复杂度为 O(n^3/64)
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e3+5;
bitset<N>dp[N];
void solve(){
int n;
cin>>n;
vector<string>s(n+1);
for(int i=1;i<=n;i++){
cin>>s[i];
s[i]=' '+s[i];
dp[i].set(i);
for(int j=1;j<=n;j++){
if(s[i][j]=='1'){
dp[i].set(j);
}
}
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
if(dp[i][k]){
dp[i]|=dp[k];
}
// dp[i][j]|=dp[i][k]|dp[k][j];
}
}
int ans=0;
for(int i=1;i<=n;i++)ans+=dp[i].count();
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T=1;
//cin>>T;
while(T--){
solve();
}
return 0;
}