环形链表 Ⅱ【LC142】

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/linked-list/jjhf6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

哈希表

• 思路：使用哈希表存放链表中的节点，找到第一个在哈希表中重复出现的结点，即为环的入口

• 2021/12/9

  /**
   * Definition for singly-linked list.
   * class ListNode {
   *     int val;
   *     ListNode next;
   *     ListNode(int x) {
   *         val = x;
   *         next = null;
   *     }
   * }
   */
  public class Solution {
      public ListNode detectCycle(ListNode head) {
          Set<ListNode> seen = new HashSet<>();  
          while(head!=null){
              if(!seen.add(head)){
                  return head;
              }
              head = head.next;
          }
          return null;      
      }
  }
  

• 复杂度分析

  • 时间复杂度：$O(N)$，其中 $N$是链表中的节点数。
  • 空间复杂度：$O(N)$

快慢指针

• 2023/07/30

• 思路：

  • 首先，由LC141可知，如果链表中存在环，那么快慢指针会在环中相遇，但相遇的位置不一定是入环口，如下图所示。设链表中环外部分的长度为a，慢指针进入环后，又走了b的距离与快指针相遇。此时，快指针已经走完了环的n圈，因此快指针走过的总距离为$$a+n(b+c)+b$$。

  • 由任意时刻，快指针走过的距离都为慢指针的2倍。因此，有
    $$a+(n+1)b+nc=2(a+b)-->a=c+(n-1)(b+c)$$

  • 可得从相遇点到入环点的距离加上n-1圈的环长，恰好等于从链表头部到入环点的距离。

  • 因此，当快慢指针相遇时，再额外用一个指针指向链表头部，随后，它和慢指针每次向后移动一个位置。最终，它们会在入环点相遇。

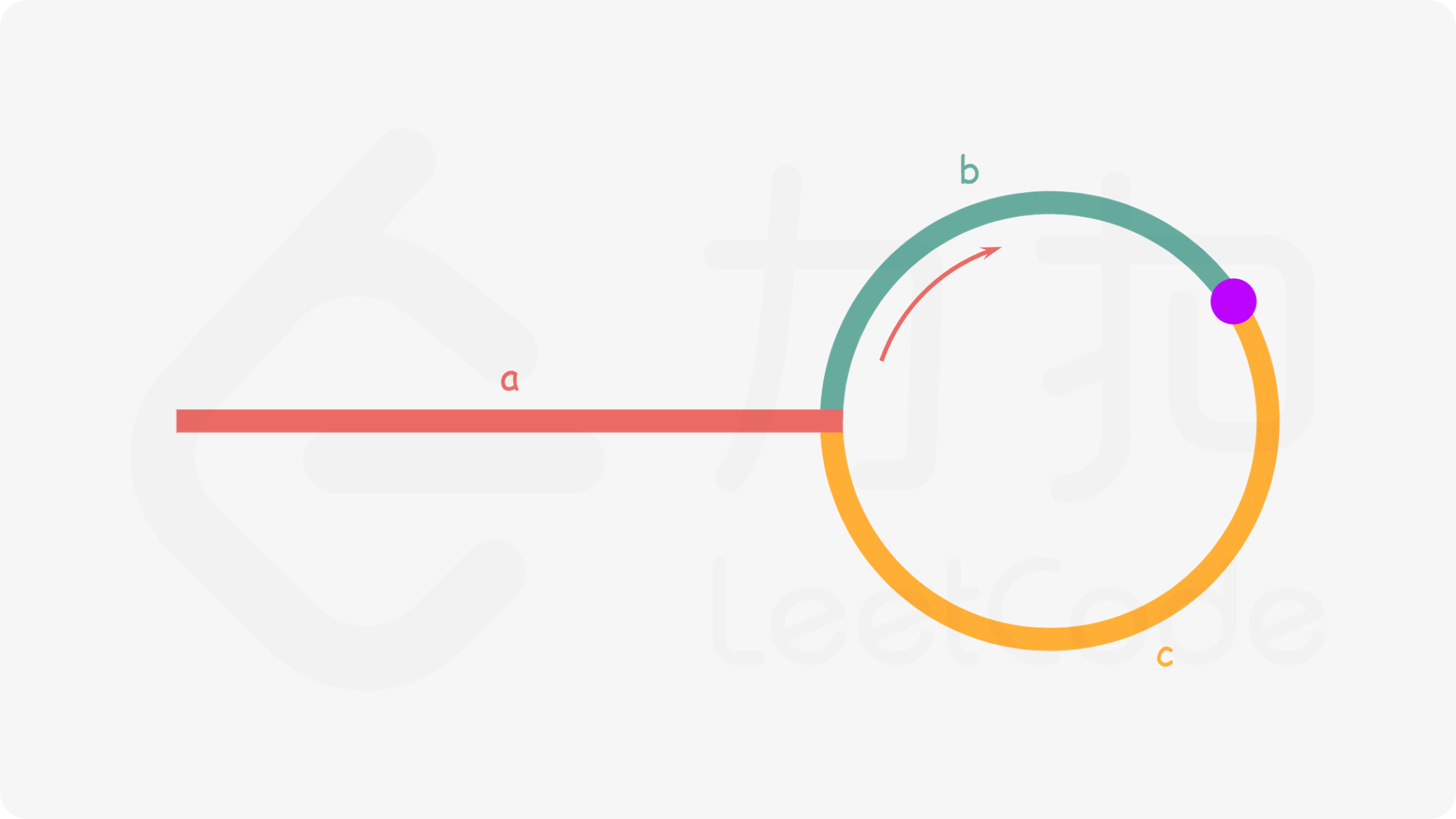
• 为什么慢指针入环第一圈没走完的时候就会和快指针相遇？

  1. 首先，快指针先进入环
  2. 当慢指针刚到达环的入口时，快指针此时在环中的某个位置（此时也可能相遇）
  3. 假设此时快慢指针的距离为x，若在步骤2相遇，则x=0
  4. 设环的周长为n，那么看成快指针追赶慢指针，需要追赶n-x个单位
  5. 快指针每次都追赶慢指针1个单位，那么慢指针走了n-x个单位，又因为x>0，则慢指针走的路程小于等于n，因此慢指针走不完一圈就会与快指针相遇

• 代码

  public class Solution {
      public ListNode detectCycle(ListNode head) {
          ListNode slowNode = head;
          ListNode fastNode = head;
          while (fastNode != null && fastNode.next != null){
              slowNode = slowNode.next;
              fastNode = fastNode.next.next;
              if (slowNode == fastNode){
                  ListNode curNode = head;
                  while (curNode != fastNode ){
                      curNode = curNode.next;
                      fastNode = fastNode.next;
                  }
                  return curNode;
              }
          }
          
          return null;
      }
  }
  

• 复杂度分析

  • 时间复杂度：$O(N)$，其中 $N$是链表中的节点数。
  • 空间复杂度：$O(1)$