七大经典比较排序算法

news2024/9/24 1:24:21

1. 插入排序 (⭐️⭐️)

🌟 思想：

直接插入排序是一种简单的插入排序法，思想是是把待排序的数据按照下标从小到大，依次插入到一个已经排好的序列中，直至全部插入，得到一个新的有序序列。例如：我们玩扑克牌的时候，每次摸进一张的新的牌我们会将其插入到合适的位置。

思路： 我们假设第一个数据有序，从第二个元素开始进行插入（最开始把前面第一个数据看作一个有序的区间），从后向前依次寻找合适位置，每次插入的时候如果当前位置不合适将当前位置向后移动一位。

InsertSort 实现：

// 插入排序
void InsertSort(int * nums , int size) {
	for (int i = 0; i < size - 1; i++) {
		// 把 [0 , end] 看作有序区间
		int end = i;
		// nums[end + 1]为需要插入的元素 使用 temp 保存
		int temp = nums[end + 1];
		// 找插入位置
		while (end >= 0 && temp < nums[end]) {
			// 把当前元素向后移动
			nums[end + 1] = nums[end];
			end--;
		}
		// 来到这里说明 temp >= nums[end] 找到插入位置
		// 插入
		nums[end + 1] = temp;
	}
}

我们可以思考一下极端情况：

  • 假设数据为 3 5 7，end 为 1，temp = 7，所以 temp < nums[end] 为 false 循环结束，执行 nums[end + 1] = temp，相当于 nums[2] = 7 而当前位置本来就是 7，不会有影响。
  • 假设数据为 3 5 1，end 为 1，temp = 1，当前 temp < nums[end] 将数据向后移动直至 3 3 5，当 end = -1循环结束，nums[end + 1] = temp 相当于 nums[0] = temp，所以最终结果为 1 3 5。

总结：

  1. 元素结合越接近有序，直接插入排序算法的时间效率就越高。
  2. 最坏时间复杂度： O ( N 2 ) O(N^2) O(N2)
  3. 接近有序或已经有序时间复杂度： O ( N ) O(N) O(N)
  4. 空间复杂度： O ( 1 ) O(1) O(1)

2.希尔排序 (⭐️⭐️⭐️)

🌟 思想：

希尔排序又称缩小增量法。希尔排序的基本思想是：先选定一个 gap (整数)，把待排序中的数据分成 gap 组（gap 距离的为同一组），并对每一组内的的数据进行插入排序。

假设 gap = 3 将下面的 10 个数分成 3 组。 {9 , 5 , 8 , 5}、{1 , 7 , 6}、{2 , 4 , 3}分别进行插入排序。当 gap 不为 1 时都是预排序，当 gap = 1时是插入排序，因为当数据接近有序的时候，插入排序的效率很高。

在这里插入图片描述

1️⃣ gap 组希尔排序： 这是希尔排序的 gap 组的一种写法，按上面的图来说，这样的写法是先走完红色组，再走蓝色组……

void ShellSort (int * nums , int size) {
	assert(nums);
	// 假设 gap = 3
	int gap = 3;
	for (int j = 0; j < gap; j++) {
		for (int i = j; i < size - gap; i+=gap) {
			int end = i;
			int temp = nums[end + gap];
			while (end >= 0 && temp < nums[end]) {
				nums[end + gap] = nums[end];
				end -= gap;
			}
			nums[end + gap] = temp;
		}
	}
}

2️⃣ gap 组希尔排序：第二种在上一种写法上进行了优化，原来是一组走完再走下一组，现在是一组一组间交替的去插入排序。

void ShellSort (int * nums , int size) {
	assert(nums);
	// 假设 gap = 3
	int gap = 3;
	for (int i = 0; i < size - gap; i++) {
		int end = i;
		int temp = nums[end + gap];
		while (end >= 0 && temp < nums[end]) {
			nums[end + gap] = nums[end];
			end -= gap;
		}
		nums[end + gap] = temp;
	}
}

ShellSort 实现：当 gap > 1 的时候都是预排序（是为了让数据更接近有序，因为直接插入排序当数据接近有序的时候是 O ( N ) O(N) O(N)），而这里 gap / 3 + 1 是为了最后一次让 gap = 1。 当 gap 越大的时候大的数会越快的到后面，但是数组越不接近有序。当 gap 越小的时候，数组越接近有序。当 gap = 1 就是直接插入排序。

void ShellSort (int * nums , int size) {
	assert(nums);
	
	int gap = size;
	while (gap > 1) {
		gap = gap / 3 + 1;
		for (int i = 0; i < size - gap; i++) {
			int end = i;
			int temp = nums[end + gap];
			while (end >= 0 && temp < nums[end]) {
				nums[end + gap] = nums[end];
				end -= gap;
			}
			nums[end + gap] = temp;
		}
	}
}

总结：

  1. 时间复杂度 ~ O ( N 1.3 ) O(N^{1.3}) O(N1.3)
  2. 空间复杂度： O ( 1 ) O(1) O(1)
  3. 希尔排序是插入排序的优化

3. 选择排序 (⭐️)

🌟 思想：

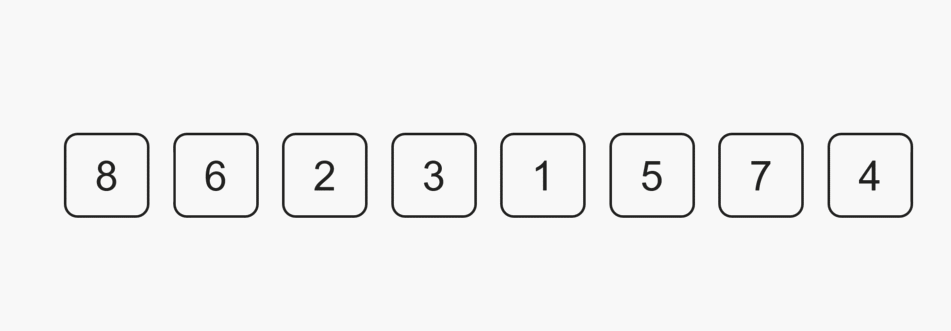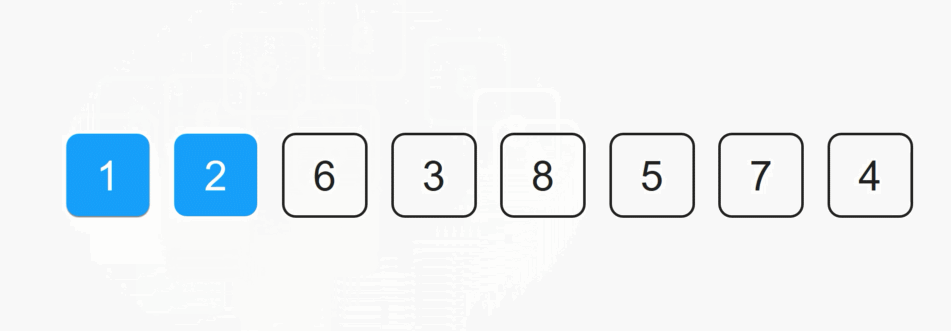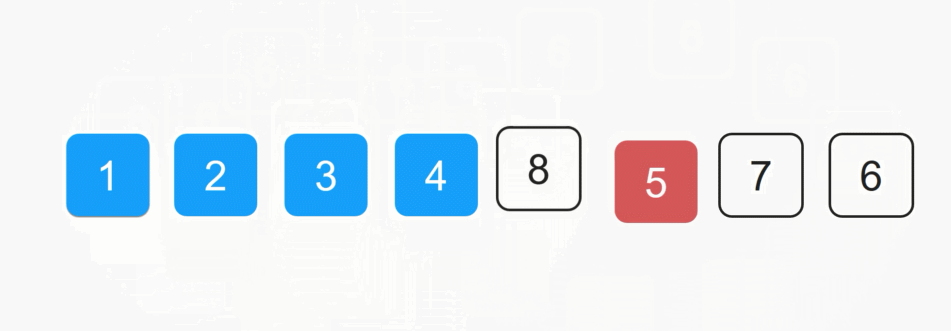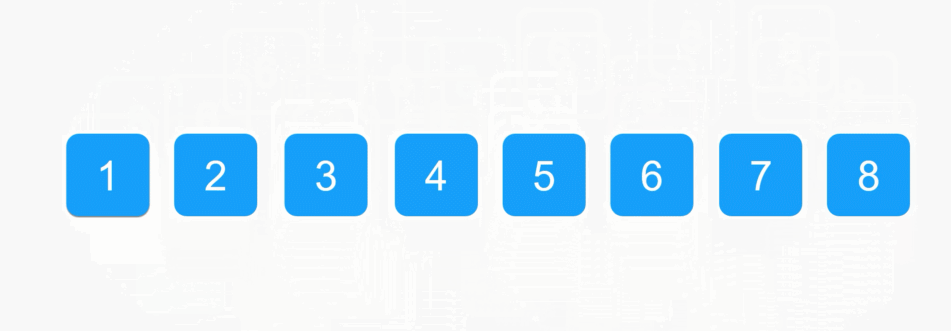
每一次从待排序的数据种选出最小或者最大的元素下标，存放在当前序列的起始位置，直到排序结束。

请添加图片描述

1️⃣SelectSort 实现：

// 选择排序
void SelectSort(int * nums , int size) {
	assert(nums);
	for (int i = 0; i < size - 1; i++) {
		int minIndex = i + 1;
		// 选数
		for (int j = i + 1; j < size; j++) {
			if (nums[j] < nums[minIndex ]) {
				minIndex = j;
			}
		}
		// 交换
		int temp = nums[minIndex];
		nums[minIndex] = nums[i];
		nums[i] = temp;
	}
}

2️⃣ SelectSort 优化： 我们可以同时选出两个数一个最大一个最小，把最小的组交换到当前区间的左边，最大的交换到区间的右边。

void SelectSort(int * nums , int size) {
	assert(nums);
	int left = 0;
	int right = size - 1;
	while (left < right) {
		// 最小值下标默认从左区间开始
		int maxIndex = left;
		int minIndex = left;
		for (int i = left + 1; i <= right; i++) {
			if (nums[i] > nums[maxIndex]) {
				maxIndex = i;
			}
			if (nums[i] < nums[minIndex]) {
				minIndex = i;
			}
		}
		// 交换
		Swap(&nums[left] , &nums[minIndex]);
		// 特殊情况：假设第一个位置就是最大值 那么做完第一次交换最小的值到最左边
		// 而最大值被交换到了原来最小值的位置
		if (left == maxIndex) {
			maxIndex = minIndex;
		}
		Swap(&nums[right] , &nums[maxIndex]);
		left++;
		right--;
	}
}

Swap 实现：

// 交换
void Swap(int* val1, int* val2) {
	int temp = *val1;
	*val1 = *val2;
	*val2 = temp;
}

总结：

  1. 选择排序比较好理解，但是效率很低，实际种很少使用。
  2. 时间复杂度 O ( N 2 ) O(N^2) O(N2)

4. 堆排序 (⭐️⭐️⭐️)

🌟 思想：

堆排序是指用堆这种数据结构所设计的一种排序思想，它是选择排序的一种，它是用堆来进行选数。升序需要建大堆，降序需要建小堆。

拿升序来举例，因为大堆的堆顶是最大的数，此时我们可以让堆顶和末尾元素交换。再让堆顶的元素向下调整（只不过此时向下调整，我们先让数组的长度减 1，因为最大的数已经到末尾的位置了，不必算入堆内）

AdjustDown 实现（大堆举例）：

// 堆的向下调整算法
void AdjustDown(int * nums , int size , int parent) {
	assert(nums);
	// 默认左孩子最大
	int child = 2 * parent + 1;
	while (child < size) {
		// 选出左右孩子最大的孩子
		if (child + 1 < size && nums[child + 1] > nums[child]) {
			child++;
		}
		// 最大的孩子比父亲还大则调整
		if (nums[child] > nums[parent]) {
			Swap(&nums[child] , &nums[parent]);
			// 继续向下搜索
			parent = child;
			child = parent * 2 + 1;
		} else {
			break;
		}
	}
}

AdjustUp 实现（大堆举例）：

// 堆的向上调整算法
void AdjustUp (int * nums , int child) {
	int parent = (child - 1) / 2;
	// 当孩子 = 0的时候已经没有父亲节点了
	while (child > 0) {
		if (nums[child] > nums[parent]) {
			Swap(&nums[child] , &nums[parent]);
			// 继续向上搜索
			child = parent;
			parent = (child - 1) / 2;
		} else {
			break;
		}
	}
}

HeapSort 实现：

// 堆排序
void HeapSort(int * nums , int size) {
	assert(nums);
	// 先建堆
	// 向上调整算法建堆
	// for (int i = 1; i < size; i++) {
		// AdjustUp(nums , i);
	// }
	
	// 向下调整算法建堆
	// 向下调整的前提是：左右子树必须都是堆
	// 所以大堆从第一个非叶子节点开始向下调整
	for (int parent = (size - 1 - 1) / 2; parent >= 0; parent--) {
		AdjustDown(nums , size , parent);
	}

	// 排序
	int end = size - 1;
	while (end > 0) {
		// 堆顶元素和末尾元素交换
		Swap(&nums[0] , &nums[end]);	
		AdjustDown(nums , end , 0);
		end--;
	}
}

总结：

  1. 堆排序的时间复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
  2. 向上调整算法建堆的时间复杂度是 O ( N ∗ l o g N ) O(N * logN) O(N∗logN)，向下调整算法建堆的时间复杂度是 O ( N ) O(N) O(N)，但是向下调整算法建堆的前提是：当前左右子树必须是堆。所以向下调整算法要从非叶子节点开始向下调整，最后一个非叶子节点就是最后一个元素的父节点 (size - 1 - 1) / 2。

5. 冒泡排序 (⭐️⭐️)

🌟 思想：

冒泡排序是交换排序的一种。所谓交换就是根据序列中两个记录下标值的比较结果来对这一对数据进行交换，当第一躺冒泡排序结束后，若是升序会把最大的数冒到最后末尾，以此类推。

BubbleSort 实现：

// 冒泡排序
void BubbleSort(int* nums, int size) {
	assert(nums);
	for (int i = 0; i < size - 1; i++) {
		for (int j = 0; j < size - 1 - i; j++) {
			if (nums[j] > nums[j + 1]) {
				Swap(&nums[j] , &nums[j + 1]);
			}
		}
	}
}

BubbleSort 优化：当数组为有序的时候，我们用 enchage 来记录，若当前这一趟一次都没有交换，则数组已经有序。

// 冒泡排序
void BubbleSort(int* nums, int size) {
	assert(nums);

	for (int i = 0; i < size - 1; i++) {
		int exchage = 1;
		for (int j = 0; j < size - 1 - i; j++) {
			if (nums[j] > nums[j + 1]) {
				exchage = 0;
				Swap(&nums[j] , &nums[j + 1]);
			}
		}
		if (exchage) {
			break;
		}
	}
}

总结：

  1. 冒泡排序是非常经典的排序
  2. 时间复杂度 O ( N 2 ) O(N^2) O(N2)

6. 快速排序 (⭐️⭐️⭐️⭐️)

🌟 思想：

快速排序是 Hoare于1962年提出的一种二叉树结构的交换排序方法。基本思想是：从待排序序列中选一个 key（通常为最左边或者最右边），按照 key 把待排序序列分成两个子序列，左序列中的元素都 < key，右序列的元素都 > key，然后左右序列重复该过程，直到所有元素都排列在对应的位置上。

在这里插入图片描述

1.hoare版本：

思路和结论：假设 key 为最左边的数，那么就要先从右边走，再走左边。假设 key 为最右边的数，那么就要从左边先走，再走右边。这样做的目的是：当 left 与 right 相遇结束的时候，让 key 位置的元素与当前相遇位置交换，而当前相遇位置一定能保证比 key 要小（或大）。 第一次快速排序相当于处理好了第一个区间，因为 key 找到了合适的位置左面的数都比 key 小，右面的数都比 key 要大，此时只需要让左右区间重复上面的过程。左右区间划分为了 [begin , keyIndex - 1] keyIndex [keyIndex + 1 , end]。递归处理即可，当左右区间只剩一个数（begin == end）或者区间不存在（begin > end）的时候为递归结束条件。

QucikSort实现：

void QuickSort(int * nums , int begin , int end) {
	
	// 只剩一个数或者区间不存在不需要处理
	if (begin >= end) {
		return;
	}

	int left = begin;
	int right = end;
	// key 默认为最左边的数字
	int keyIndex = left;
	while (left < right) {
		// 右边先走，找小
		while (left < right && nums[right] >= nums[keyIndex]) {
			right--;
		}
		// 左边找大
		while (left < right && nums[left] <= nums[keyIndex]) {
			left++;
		}
		// 交换
		Swap(&nums[left] , &nums[right]);
	}
	// 相遇位置和 keyIndex 交换
	Swap(&nums[keyIndex] , &nums[left]);
	// 更改 keyIndex
	keyIndex = left;
	
	QuickSort(nums , begin , keyIndex - 1);
	QuickSort(nums , keyIndex + 1, end);
}

💬 思考问题：

  1. nums[left] <= nums[keyIndex] 和 nums[right] >= nums[keyIndex] 这里为什么要使用 = ，不使用 = 可以吗？结论是不可以。

    在这里插入图片描述

  1. 为什么右边和左边走的时候要加上 left < right？

在这里插入图片描述

  1. 为什么 key 如果是左边的数就要先从右边走呢？左边先走可以吗？结论是不可以。
    在这里插入图片描述

2.挖坑版本：

思路：先将最左面的数据存在一个临时变量 key 中，这样当前 key 这个位置就是一个坑位。右面 right 找小，找到之后把小的数填到当前坑中 nums[keyIndex] = nums[right]，此时更换坑的位置 keyIndex = right。左面 left 找大，找到之后把大的数继续填到当前坑中 nums[keyIndex] = nums[left]，此时继续更换坑的位置 keyIndex = left。当 left 与 right 相遇时在把 key 填入相遇（坑位）位置。

QucikSort实现：

void QuickSort(int * nums , int begin , int end) {
	// 只剩一个数或者区间不存在不需要处理
	if (begin >= end) {
		return;
	}
	
	int left = begin;
	int right = end;
	// 保存当前坑的元素
	int key= nums[left];
	// 坑位
	int keyIndex = left;
	while (left < right) {
		while (left < right && nums[right] >= key) {
			right--;
		}
		// 填坑
		nums[keyIndex] = nums[right];
		// 更换坑的位置
		keyIndex = right;
		while (left < right && nums[left] <= key) {
			left++;
		}
		// 填坑
		nums[keyIndex] = nums[left];
		// 更换坑的位置
		keyIndex = left;
	}
	// 循环结束填入当前坑位
	nums[keyIndex] =  key;

	QuickSort(nums , begin , keyIndex - 1);
	QuickSort(nums , keyIndex + 1, end);
}

注：同样一组数，使用 hoare 思想和挖坑法思想进行一轮快排的结果是不同的。

例如：{6 , 1 , 2 , 7 , 9 , 3 , 4 , 5 , 10 , 8}

  1. hoare： 第一次交换 {6 , 1 , 2 , 5 , 9 , 3 , 4 , 7 , 10 , 8}、第二次交换 {6 , 1 , 2 , 5 , 4 , 3 , 9 , 7 , 10 , 8}、循环结束相遇位置与 keyIndex 位置交换 {3 , 1 , 2 , 5 , 4 , 6 , 9 , 7 , 10 , 8} 最终结果。

  2. 挖坑法： 第一次挖坑 {5 , 1 , 2 , 7 , 9 , 3 , 4 , (5) , 10 , 8}、第二次 {5 , 1 , 2 , (7) , 9 , 3 , 4 , 7 , 10 , 8}、第三次 {5 , 1 , 2 , 4 , 9 , 3 , (4) , 7 , 10 , 8}、第四次 {5 , 1 , 2 , 4 , (9) , 3 , 9 , 7 , 10 , 8}、第五次 {5 , 1 , 2 , 4 , 3 , (3) , 9 , 7 , 10 , 8}、循环结束把当前坑位填入 key 最终结果是 {5 , 1 , 2 , 4 , 3 , 6 , 9 , 7 , 10 , 8}。

3.前后指针版本：

思路： 定义一个 prev 和 cur，cur 找比 key 要小的数，若找到则 ++prev 和 cur 当前下标的元素进行交换，这样做有一种把小的数翻到前面来，大的往后推。而 prev 后面的数都要比 key 大，最终 cur 越界循环结束，再把 keyIndex 位置和 prev 位置的元素进行交换。

QucikSort 实现：

void QuickSort(int * nums , int begin , int end) {
	// 只剩一个数或者区间不存在不需要处理
	if (begin >= end) {
		return;
	}
	
	int prev = begin;
	int cur = prev + 1;
	int keyIndex = begin;
	while (cur <= end) {
		if (nums[cur] < nums[keyIndex] && ++prev != cur) {
			Swap(&nums[prev] , &nums[cur]);
		}
		cur++;
	}
	Swap(&nums[prev] , &nums[keyIndex]);
	keyIndex = prev;
	
	QuickSort(nums , begin , keyIndex - 1);
	QuickSort(nums , keyIndex + 1, end);
}

🌟 快排优化

💬 为什么要优化？

因为 key 会影响快排的效率，如果每次的 key 都是中间那个值那么每次都是二分，若每次的 key 都是最小的，最坏情况下快排的时间复杂度 O ( N 2 ) O(N^2) O(N2)。最大的问题是会引起 栈溢出。

1.三数取中优化：

思路： 第一个数和中间还有最后的数，选不是最大也不是最小的数。三数取中主要体现在数据已经有序的情况下。

getMidIndex 实现：

int getMidIndex(int* nums, int begin, int end) {
	int midIndex = (begin + end) / 2;
	if (nums[begin] > nums[midIndex]) {
		// nums[begin] > nums[minIndex]
		if (nums[midIndex] > nums[end]) {
			// nums[begin] > nums[minIndex] > nums[end]
			return midIndex;
		}
		else if (nums[begin] > nums[end]) {
			// nums[begin] > nums[minIndex]
			// nums[end] >= nums[minIndex]
			// nums[begin] > nums[end]
			return end;
		}
		else {
			// nums[begin] > nums[minIndex]
			// nums[end] >= nums[minIndex]
			// nums[begin] <= nums[end]
			return begin;
		}
	}
	else {
		// nums[begin] <= nums[minIndex]
		if (nums[begin] > nums[end]) {
			// nums[begin] <= nums[minIndex]
			// nums[begin] > nums[end]
			return begin;
		}
		else if (nums[midIndex] > nums[end]) {
			// nums[begin] <= nums[minIndex]
			// nums[begin] <= nums[end]
			// nums[minIndex] > nums[end]
			return end;
		}
		else {
			// nums[begin] <= nums[minIndex]
			// nums[begin] <= nums[end]
			// nums[minIndex] <= nums[end]
			return midIndex;
		}
	}
}

2.小区间优化：

思路： 若只剩最后 10 - 20 个数，还使用快速排序的递归就有点不太划算了。所以当区间较小的时候，就不再使用递归继续划分小区间。考虑直接用其他排序对小区间处理，而希尔排序和堆排序对于数据量小的时候也不太优，所以在简单排序中，插入排序适应性最强。 小区间优化体现在减少递归的调用次数。

QuickSort 优化实现：

void QuickSort(int* nums, int begin, int end) {
	// 只剩一个数或者区间不存在不需要处理
	if (begin >= end) {
		return;
	}

	if (end - begin > 15) {
		int prev = begin;
		int cur = prev + 1;
		int keyIndex = begin;
		// 三数取中优化
		int midIndex = getMidIndex(nums, begin, end);
		Swap(&nums[keyIndex], &nums[midIndex]);

		while (cur <= end) {
			if (nums[cur] < nums[keyIndex] && ++prev != cur) {
				Swap(&nums[prev], &nums[cur]);
			}
			cur++;
		}
		Swap(&nums[prev], &nums[keyIndex]);
		keyIndex = prev;

		QuickSort(nums, begin, keyIndex - 1);
		QuickSort(nums, keyIndex + 1, end);
	} 
	else {
		// 小区间优化
		// 插入排序
		InsertSort(nums + begin  , end - begin + 1);
	}
}

🌟 快排非递归

QuickSortNoneR 非递归实现：

// 快排非递归（使用栈）
void QucikSortNoneR(int* nums, int begin, int end) {
	assert(nums);

	Stack stack;
	StackInit(&stack);
	// 区间进栈
	StackPush(&stack , end);
	StackPush(&stack, begin);
	while (!StackEmpty(&stack)) {
		// 取出左右区间
		int left = StackTop(&stack);
		StackPop(&stack);
		int right = StackTop(&stack);
		StackPop(&stack);
		
		// 快排
		int keyIndex = left;
		int prev = left;
		int cur = prev + 1;
		while (cur <= right) {
			if (nums[cur] < nums[keyIndex] && ++prev != cur) {
				Swap(&nums[prev], &nums[cur]);
			}
			cur++;
		}
		Swap(&nums[prev], &nums[keyIndex]);
		keyIndex = prev;

		// [left , keyIndex - 1] keyIndex [keyIndex + 1 , right]

		if (keyIndex + 1 < right) {
			// 区间存在 入栈
			StackPush(&stack, right);
			StackPush(&stack, keyIndex + 1);
		}

		if (left < keyIndex - 1) {
			// 区间存在 入栈
			StackPush(&stack, keyIndex - 1);
			StackPush(&stack, left);
		}
	}

	StackDestroy(&stack);
}

总结：

  1. 时间复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
  2. 空间复杂度 O ( l o g N ) O(logN) O(logN)

7. 归并排序 (⭐️⭐️⭐️)

🌟 思想：

归并排序是建立在归并操作上的一种有效的排序算法，是分治的一个典型的应用。将两个有序的子序列归并得到完全有序的序列。归并排序要借助额外的空间。

MergeSort 递归实现：

void merge(int* nums, int begin, int end, int* temp) {

	// 区间只有一个数或者不存在
	if (begin >= end) {
		return;
	}
	
	int midIndex = (begin + end) / 2;

	// [begin , midIndex] [minIndex + 1 , end]
	merge(nums , begin , midIndex , temp);
	merge(nums , midIndex + 1 , end , temp);

	// 归并
	int leftBegin = begin;
	int leftEnd = midIndex;
	int rightBegin = midIndex + 1;
	int rightEnd = end;
	int i = leftBegin;
	while (leftBegin <= leftEnd && rightBegin <= rightEnd) {
		if (nums[leftBegin] < nums[rightBegin]) {
			temp[i++] = nums[leftBegin++];
		}
		else {
			temp[i++] = nums[rightBegin++];
		}
	}

	// 左区间还存在
	while (leftBegin <= leftEnd) {
		temp[i++] = nums[leftBegin++];
	}

	// 右区间还存在
	while (rightBegin <= rightEnd) {
		temp[i++] = nums[rightBegin++];
	}

	// 拷贝回原数组
	memcpy(nums + begin , temp + begin, (end - begin + 1) * sizeof(int));
}

// 归并排序
void MergeSort(int* nums, int size) {
	assert(nums);

	int* temp = (int*)malloc(sizeof(int) * size);
	assert(temp);

	merge(nums , 0 , size - 1 , temp);

	free(temp);
}

🌟 归并非递归

MergeSort 非递归实现：

// 归并排序非递归
void MergeSortNoneR(int* nums, int size) {
	assert(nums);

	int* temp = (int*)malloc(sizeof(int) * size);
	assert(temp);

	int gap = 1;
	while (gap < size) {
		for (int i = 0; i < size; i += 2 * gap) {
			int leftBegin = i;
			int leftEnd = i + gap - 1;
			int rightBegin = i + gap;
			int rightEnd = i + 2 * gap - 1;

			// 检查边界
			if (leftEnd >= size) {
				// 修正左区间
				leftEnd = size - 1;
				// 让右区间不存在
				rightBegin = size + 1;
				rightEnd = size;
			}
			else if (rightBegin >= size) {
				rightBegin = size + 1;
				rightEnd = size;
			}
			else if (rightEnd >= size) {
				rightEnd = size - 1;
			}

			// 归并
			int j = leftBegin;
			while (leftBegin <= leftEnd && rightBegin <= rightEnd) {
				if (nums[leftBegin] < nums[rightBegin]) {
					temp[j++] = nums[leftBegin++];
				}
				else {
					temp[j++] = nums[rightBegin++];
				}
			}

			// 左区间还存在
			while (leftBegin <= leftEnd) {
				temp[j++] = nums[leftBegin++];
			}

			// 右区间还存在
			while (rightBegin <= rightEnd) {
				temp[j++] = nums[rightBegin++];
			}

		}
		memcpy(nums, temp, sizeof(int) * size);
		gap *= 2;
	}


	free(temp);
}

总结：

  1. 时间复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
  2. 空间复杂度 O ( N ) O(N) O(N)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/810857.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Doc as Code (3)：业内人士的观点

Doc as Code (3)：业内人士的观点

作者 | Anne-Sophie Lardet 在技术传播国际会议十周年之际&#xff0c;Fluid Topics 的认证技术传播者和功能顾问 Gaspard上台探讨了“docOps 作为实现Doc as Code的中间结构”的概念。在他的演讲中&#xff0c;观众提出了几个问题&#xff0c;我们想分享Gaspard的见解&#x…
阅读更多...
深入学习 Redis - 渐进式遍历 scan 命令、数据库管理命令

深入学习 Redis - 渐进式遍历 scan 命令、数据库管理命令

目录 前言 一、scan 命令 二、数据库管理命令 select dbsize flushdb / flushall 前言 之前我们所了解到的 keys * 是一次性把整个 redis 中所有的 key 都获取到&#xff0c;但是整个操作比较危险&#xff0c;可能会一下子的都太多的 key&#xff0c;阻塞 redis 服务器. …
阅读更多...
NLP（六十三）使用Baichuan-7b模型微调人物关系分类任务

NLP（六十三）使用Baichuan-7b模型微调人物关系分类任务

任务介绍 人物关系分类指的是对文本中的两个人物&#xff0c;在特定的关系列表中&#xff0c;判断他们之间的人物关系。以样本亲戚 1837年6月20日&#xff0c;威廉四世辞世&#xff0c;他的侄女维多利亚即位。为例&#xff0c;其中亲戚为人物关系&#xff0c;威廉四世为实体1&a…
阅读更多...
vins调试的注意事项

vins调试的注意事项

1、摄像头的内参和畸变矫正系数 这个系数不对&#xff0c;没法做&#xff0c;因为下一步没法做对。这个会导致系统无法初始化。 2、对畸变的像素点&#xff0c;求得归一化坐标的方法 理解不同矫正模型的原理&#xff0c;确保矫正对了&#xff0c;得到z1平面的去畸变点。 3、摄…
阅读更多...
python皮卡丘编程代码教程,用python打印皮卡丘

python皮卡丘编程代码教程,用python打印皮卡丘

大家好&#xff0c;小编来为大家解答以下问题&#xff0c;如何用print函数打印一只皮卡丘&#xff0c;用python如何打印丘比特之心&#xff0c;现在让我们一起来看看吧&#xff01;
阅读更多...
CCL 2023 电信网络诈骗案件分类评测-第一名方案

CCL 2023 电信网络诈骗案件分类评测-第一名方案

1 任务内容 1.1 任务背景 2022年12月1日起&#xff0c;新出台的《反电信网络诈骗犯罪法》正式施行&#xff0c;表明了我国治理当前电信网络诈骗乱象的决心。诈骗案件分类问题是打击电信网路诈骗犯罪过程中的关键一环&#xff0c;根据不同的诈骗方式、手法等将其分类&#xff…
阅读更多...
13个ChatGPT类实用AI工具汇总

13个ChatGPT类实用AI工具汇总

在ChatGPT爆火后&#xff0c;各种工具如同雨后春笋一般层出不穷。以下汇总了13种ChatGPT类实用工具&#xff0c;可以帮助学习、教学和科研。 01 / ChatGPT for google/ 一个浏览器插件&#xff0c;可搭配现有的搜索引擎来使用 最大化搜索效率&#xff0c;对搜索体验的提升相…
阅读更多...
【机器学习】Linear Regression

【机器学习】Linear Regression

Model Representation 1、问题描述2、表示说明3、数据绘图4、模型函数5、预测总结附录 1、问题描述 一套 1000 平方英尺 (sqft) 的房屋售价为300,000美元&#xff0c;一套 2000 平方英尺的房屋售价为500,000美元。这两点将构成我们的数据或训练集。面积单位为 1000 平方英尺&a…
阅读更多...
C++ 类和对象篇(零) 面向过程 和 面向对象

C++ 类和对象篇(零) 面向过程 和 面向对象

目录 一、面向过程 二、面向对象 三、两种编程思想的比较 四、C和C 一、面向过程 1.是什么&#xff1f; 是一种以解决问题的过程为中心的编程思想。即先分析出解决问题所需要的步骤&#xff0c;然后用函数把这些步骤一步一步实现。 2.为什么&#xff1f; 面向过程就纯粹是分析…
阅读更多...
基于x-scan扫描线的3D模型渲染算法

基于x-scan扫描线的3D模型渲染算法

基于x-scan算法实现的z-buffer染色。c#语言&#xff0c;.net core framework 3.1运行。 模型是读取3D Max的obj模型。 x-scan算法实现&#xff1a; public List<Vertex3> xscan() {List<Vertex3> results new List<Vertex3>();SurfaceFormula formula g…
阅读更多...
SAP 自定义BADI增强点

SAP 自定义BADI增强点

应用场景 标准化代码中预留客制化部分&#xff0c;保证代码主体完整性&#xff0c;可以在预留增强位置预留两种类型的增强处理&#xff0c;其一为标准增强类型的&#xff0c;增强部分代码属于增加的逻辑&#xff0c;其二对于部分多样化的逻辑&#xff0c;使用优先执行默认逻辑&…
阅读更多...
Java常用API：Object、Objects、包装类

Java常用API：Object、Objects、包装类

Object类API toString 返回字符串类型 equals 默认比较的是地址 此时返回的是 false 可以在类中重写equals 方法 比较内容 如果内容一样就返回true clone 不能在测试类中用&#xff0c;必须在创建的类中重写克隆方法 还必须要有接口&#xff0c;说明这个对象有这个能力克隆 …
阅读更多...
增量预训练baichuan-13b-chat遇到的那些坑

增量预训练baichuan-13b-chat遇到的那些坑

文章目录 前言资源deepspeed一、训练的坑二、推理的坑三、继续训练的坑总结前言 资源 单机两4090，如图 单卡24G，baichuan-13b-chat单卡推理需要至少26G，因此仅用一张卡，我们是无法加载百川13B的模型，所以，无论是推理还是训练，我们都必须并行！ deepspeed 核心思想…
阅读更多...
主干网络篇 | YOLOv8 更换主干网络之 VanillaNet |《华为方舟实验室最新成果》

主干网络篇 | YOLOv8 更换主干网络之 VanillaNet |《华为方舟实验室最新成果》

论文地址：https://arxiv.org/pdf/2305.12972.pdf 代码地址：https://github.com/huawei-noah/VanillaNet 在基础模型的核心是“多样性即不同”，这一哲学在计算机视觉和自然语言处理方面取得了惊人的成功。然而，优化和Transformer模型固有的复杂性带来了挑战，需要转向简洁性…
阅读更多...
Python-Python基础综合案例--数据可视化 - 地图可视化

Python-Python基础综合案例--数据可视化 - 地图可视化

版本说明 当前版本号[20230729]。 版本修改说明20230729初版 目录 文章目录 版本说明目录知识总览图Python基础综合案例--数据可视化 - 地图可视化基础地图使用案例效果视觉映射器 疫情地图-国内疫情地图案例效果实操设置全局配置选项 疫情地图-省级疫情地图案例效果实操 知…
阅读更多...
spring拦截器 与统一格式

spring拦截器 与统一格式

目录 前言模拟拦截器拦截器的实现原理什么是动态代理? 什么是静态代理静态代理与动态代理的区别两种常用的动态代理方式基于接口的动态代理基于类的动态代理 JDK Proxy 与 CGlib的区别 其他 统⼀访问前缀添加统⼀异常处理统⼀数据返回格式 前言 之前博客讲述了 , 关于SpringA…
阅读更多...
Kotlin～Memento备忘录模式

Kotlin～Memento备忘录模式

概念 备忘录模式是一种行为型设计模式&#xff0c;用于捕获和存储对象的内部状态&#xff0c;并在需要时将对象恢复到之前的状态。 备忘录模式允许在不暴露对象内部实现细节的情况下&#xff0c;对对象进行状态的保存和恢复。 角色介绍 Originator&#xff1a;原发器&#x…
阅读更多...
7.事件类型

7.事件类型

7.1鼠标事件 案例-轮播图点击切换 需求&#xff1a;当点击左右的按钮&#xff0c;可以切换轮播图 分析: ①右侧按钮点击&#xff0c;变量&#xff0c;如果大于等于8&#xff0c;则复原0 ②左侧按钮点击&#xff0c;变量–&#xff0c;如果小于0&#xff0c;则复原最后一张 ③鼠…
阅读更多...
Zotero ubuntu2023安装 关联 ubuntu文献翻译

Zotero ubuntu2023安装 关联 ubuntu文献翻译

一、准备下载的软件&#xff1a; Zotero | Downloads 1. Zotero-6.0.26_linux-x86_64.tar.bz2 下面是插件 zotfile-5.1.2-fx.xpi zotero-pdf-translate.xpi jasminum-v0.2.6.xpi 2.2.5 Tampermonkey 4.11.crx 所准备的文件&#xff0c;都已经在这个链接的压缩包下面 …
阅读更多...
【机器学习】Multiple Variable Linear Regression

【机器学习】Multiple Variable Linear Regression

Multiple Variable Linear Regression 1、问题描述1.1 包含样例的X矩阵1.2 参数向量 w, b 2、多变量的模型预测2.1 逐元素进行预测2.2 向量点积进行预测 3、多变量线性回归模型计算损失4、多变量线性回归模型梯度下降4.1 计算梯度4.2梯度下降 首先&#xff0c;导入所需的库 im…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023