CCF CSP认证——201312

news2024/10/7 1:29:22

 

文章目录

  • 201312-1 出现次数最多的数
  • 201312-2 ISBN号码
  • 201312-3 最大的矩形
  • 201312-4 有趣的数
  • 201312-5 I’m stuck!

 
 

  

201312-1 出现次数最多的数

题目链接

1

数据量较小，且数据范围也比较小。可以直接暴力，通过设置数组记录下标数据出现的次数，最后遍历记录数组获取出现最多出现次数的数字。

#include<iostream>
using namespace std;

int main(){//暴力 
	int n, flag[10001] = {0};
	scanf("%d", &n);
	for(int i = 0; i < n; i ++){
		int a;
		scanf("%d", &a);
		flag[a] ++;
	}
	int m = 0;
	for(int i = 1; i <= 10000; i ++)
		if(flag[m] < flag[i])
			m = i;
	printf("%d", m);
	return 0;
}

 
 

 
 

 
 

201312-2 ISBN号码

题目链接
2

简答题
挨个接受ISBN号码或者分四个数接收都可以。

#include<iostream>
#include<algorithm>
#include<stack>
using namespace std;

int main(){//注意标识码为X(也就是10)的情况 
	int a[10], b = 0;
	char c;
	scanf("%1d-%1d%1d%1d-%1d%1d%1d%1d%1d-%c", &a[0], &a[1], &a[2], &a[3], &a[4], &a[5], &a[6], &a[7], &a[8], &c);
	for(int i = 0; i < 9; i ++)
		b += a[i] * (i + 1);
	b %= 11;
	if(b == (c == 'X' ? 10 : c - '0'))
		printf("Right");
	else
		printf("%1d-%1d%1d%1d-%1d%1d%1d%1d%1d-%c", a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8], b == 10 ? 'X' : b + '0');
	return 0;
}

 
 

 
 

 
 

201312-3 最大的矩形

题目链接
3

①
数据量较少，可以直接暴力求解。
时间复杂度：O(n2)

#include<iostream>
#include<algorithm>
#include<stack>
using namespace std;

int main(){//暴力 
	int n, a[1000], m = 0;
	scanf("%d", &n);
	for(int i = 0; i < n; i ++)
		scanf("%d", &a[i]) ;
	for(int i = 0; i < n; i ++){
		int t = a[i];
		for(int j = i; j < n; j ++){
			t = min(t, a[j]);
			m = max(m, (j - i + 1) * t);
		}
	}
	printf("%d", m);
	return 0;
}

②
单调栈（递增）
通过单调递增栈实现

#include<iostream>
#include<algorithm>
#include<stack>
using namespace std;

int main(){//单调栈(递增)
	int n, a[1000], m = 0;
	scanf("%d", &n);
	for(int i = 0; i < n; i ++)
		scanf("%d", &a[i]) ;
	a[n] = 0;
	stack<int> s;
	for(int i = 0; i <= n; i ++){
		if(s.empty() || a[s.top()] <= a[i])
			s.push(i);
		else{
			int t = 0;
			while(!s.empty() && a[s.top()] > a[i]){
				t = s.top();
				s.pop();
				m = max(m, (i - t) * a[t]);//i - t指的是当前矩阵的宽度，a[t]是当前高度
				//实现单调递增栈
			} 
			s.push(t);
			a[t] = a[i];
		}
	}
	printf("%d", m);
	return 0;
}

关键应该是下述两行代码难以理解
s.push(t);
a[t] = a[i];
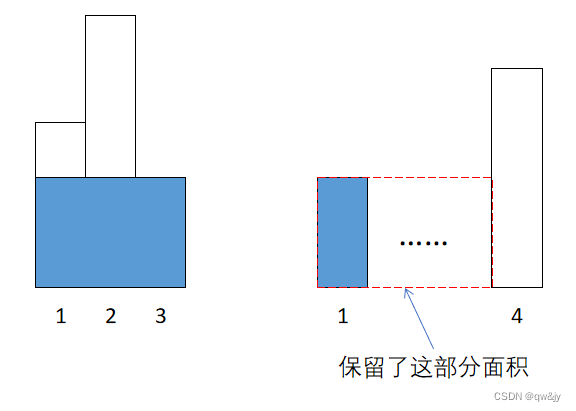
为什么要将最后出栈的位置再次入栈呢？因为构建的是递增栈所以前面栈的那些高度也是可以达到当前的高度要求的，所以将最后出栈的位置入栈就可以将前面的面积留存，不至于出现面积损失。如下所示。
分析

③
单调栈

#include<iostream>
#include<algorithm>
#include<stack>
using namespace std;

int main(){//单调栈 
	int n, a[1000], m = 0;
	scanf("%d", &n);
	for(int i = 0; i < n; i ++)
		scanf("%d", &a[i]) ;
	a[n] = 0;
	stack<int> s;
	for(int i = 0; i <= n; i ++){
		if(s.empty() || a[s.top()] < a[i])
			s.push(i);
		else{
			int t = s.top();
			s.pop();
			int area = a[t] * (s.empty() ? i : i - s.top() - 1);
			m = max(m, area);
			-- i;//不移动i，后面还有有个 i++ 
		}
	}
	printf("%d", m);
	return 0;
}

 
 

 
 

 
 

201312-4 有趣的数

题目链接
4

动态规划
第n位所放置的数一定与前n-1位放置的数有关（6种情况）
前i位处于该状态个数 状态（全为） 前i+1位处于该状态个数

状态数字转移方程情况分析
a21如果前i+1位为2，则前i位一定为2
b2，0b*2+a如果前i+1位为2，0，则
    前i位全为2，第i+1位为0
    前i位为2，0混合串，第i+1位为2或0
c2，3c+a如果前i+1位为2，3，则
    前i位全为2，第i+1位为3
    前i位为2，3混合串，第i+1位为3
d2，0，1d*2+b如果前i+1位为2，0，1，则
    前i位为2，0，第i+1位为1
    前i位为2，0，1，第i+1位为2或1
e2，0，3e*2+c+b如果前i+1位为2，0，3，则
    前i位为2，0，第i+1位为3
    前i位为2，3，第i+1位为0
    前i位为2，0，3，第i+1位为0或3
f2，0，3，1f*2+e+d如果前i+1位为2，0，3，1，则
    前i位为2，0，1，第i+1位为3
    前i位为2，0，3第i+1位为1
    前i位为2，0，3，1第i+1位为1或3
#include<iostream>
using namespace std;

long long a, b, c, d, e, f; 

int main(){
	//第n位所放置的数一定与前n-1位放置的数有关（6种情况） 
	/*前i位处于该状态个数	状态（全为）	前i+1位处于该状态个数*/
	a = 1;
	b = c = d = e = f = 0;
	int n;
	scanf("%d", &n);
	for(int i = 1; i < n; i ++){
		long long xb = b * 2 + a;
		long long xc = c + a;
		long long xd = d * 2 + b;
		long long xe = e * 2 + b + c;
		long long xf = f * 2 + d + e;
		
		b = xb % 1000000007LL;
		c = xc % 1000000007LL;
		d = xd % 1000000007LL;
		e = xe % 1000000007LL;
		f = xf % 1000000007LL;
	}
	printf("%lld", f);
	return 0;
}

 
 

 
 

 
 

201312-5 I’m stuck!

题目链接
5

dfs深度优先搜索（暴力）
通过dfs将所有S可以到达的点都标记上
同通过dfs将S不能达到的点都试一下是否可以到达T，不可以到达则数量+1

#include<iostream>
#include<vector>
#include<cstring>
using namespace std;

int n, m;//地图行列数
bool flag[50][50], flag1[50][50];//flag1存储S可以到达的点，true为可以到达的点，false为不可以到达的点
int d[][2] = {-1, 0, 1, 0, 0, -1, 0, 1};//移动方向
vector<string> map;//存储地图
int si, sj, ti, tj;//存储S和T的位置

void dfs(int x, int y){//深度优先搜索
	int xx, yy;
	flag[x][y] = 1;//标记该点已到达
	
	if(map[x][y] == '+' || map[x][y] == 'S' || map[x][y] == 'T'){//可以上下左右移动的点
		for(int i = 0; i < 4; i ++){
			xx = x + d[i][0];
			yy = y + d[i][1];
			if(xx >= 0 && xx < n && yy >= 0 && yy < m && !flag[xx][yy] && map[xx][yy] != '#')//可以走的点
				dfs(xx, yy);
		}
	}
	else if(map[x][y] == '-'){//可以左右移动的点
		for(int i = 2; i < 4; i ++){
			xx = x + d[i][0];
			yy = y + d[i][1];
			if(xx >= 0 && xx < n && yy >= 0 && yy < m && !flag[xx][yy] && map[xx][yy] != '#')
				dfs(xx, yy);
		}
	}
	else if(map[x][y] == '|'){//可以上下移动的点
		for(int i = 0; i < 2; i ++){
			xx = x + d[i][0];
			yy = y + d[i][1];
			if(xx >= 0 && xx < n && yy >= 0 && yy < m && !flag[xx][yy] && map[xx][yy] != '#')
				dfs(xx, yy);
		}
	}
	else if(map[x][y] == '.'){//只能向下移动
		xx = x + d[1][0];
		yy = y + d[1][1];
		if(xx >= 0 && xx < n && yy >= 0 && yy < m && !flag[xx][yy] && map[xx][yy] != '#')
			dfs(xx, yy);
	}
}

int main(){//暴力 
	scanf("%d %d", &n, &m);
	for(int i = 0; i < n; i ++){
		string s;
		cin >> s;
		map.push_back(s);
	}
	for(int i = 0; i < n; i ++)
		for(int j = 0; j < m; j ++)
			if(map[i][j] == 'S')
				si = i, sj = j;
			else if(map[i][j] == 'T')
				ti = i, tj = j;
	
	dfs(si, sj);
	memcpy(flag1, flag, sizeof(flag));
	
	if(flag[ti][tj]){
		int cnt = 0;
		for(int i = 0; i < n; i ++)
			for(int j = 0; j < m; j ++){
				if(flag1[i][j]){
					memset(flag, 0, sizeof(flag));
					dfs(i, j);
					if(!flag[ti][tj])
						cnt ++;
				}
			}
		printf("%d", cnt);
	}
	else
		printf("I'm stuck!");
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/80777.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C/C++关键字

C/C++关键字

C/C关键字【1】extern "C"【2】asm【3】关键字auto【4】break语句【5】catch 语句【6】关键字class【7】关键字const【8】#if【9】#pragma once【10】#pragma pack(1)【11】#pragma pack(4)【12】explicit【】 continue语句【13】关键字enum【14】friend【15】goto语…
阅读更多...
【springboot进阶】基于starter项目构建（二）构建starter项目-web

【springboot进阶】基于starter项目构建（二）构建starter项目-web

目录 一、创建 web-spring-boot-starter 项目 二、添加 pom 文件依赖 三、构建配置 1. rest模板配置 RestTemplateConfig 2. 统一异常处理 BackendGlobalExceptionHandler 3. 统一返回数据结构 4. jwt鉴权处理 5. 请求日志切面处理 WebLogAspect 6. 邮件配置 BackendM…
阅读更多...
mysql数据同步到elasticsearch数据解决方案

mysql数据同步到elasticsearch数据解决方案

mysql数据同步到elasticsearch数据解决方案 问题场景 1.分库分表后多关联或者多条件查找效率低下&#xff0c;例如2b场景的查询&#xff0c;导出等需要多条件查询&#xff0c;继续用分库分表话效率低下。 2.数据量太多需要转移非关系型数据库elasticsearch存储 3.其他数据转…
阅读更多...
AI 实战篇 ｜基于 AI开放平台实现 【植物识别】 功能，成为行走的百科全书

AI 实战篇 ｜基于 AI开放平台实现 【植物识别】 功能，成为行走的百科全书

&#x1f3ac; 博客主页&#xff1a;https://xiaoy.blog.csdn.net &#x1f3a5; 本文由 呆呆敲代码的小Y 原创&#xff0c;首发于 CSDN&#x1f649; &#x1f384; 学习专栏推荐&#xff1a;Unity系统学习专栏 &#x1f332; 游戏制作专栏推荐&#xff1a;游戏制作 &…
阅读更多...
代码随想录刷题记录day40 爬楼梯+零钱兑换+完全平方数·

代码随想录刷题记录day40 爬楼梯+零钱兑换+完全平方数·

代码随想录刷题记录day40 爬楼梯零钱兑换完全平方数 参考&#xff1a;代码随想录 70. 爬楼梯 思想 当作完全背包问题&#xff0c;物品是1&#xff0c;2&#xff0c;可以无限次取用&#xff0c;背包的容量是n 1.dp[j]表示容量为j的背包&#xff0c;装满有dp[j]次 2.dp[j]dp…
阅读更多...
【图像处理】opencv | 图像的二值化操作| cv2.threshold() | cv2.adaptiveThreshold()

【图像处理】opencv | 图像的二值化操作| cv2.threshold() | cv2.adaptiveThreshold()

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录前言一、cv2.threshold()阈值操作函数1.1、初见1.2、阈值不同时的效果二、cv2.adaptiveThreshold()自适应阈值操作函数2.1、初见2.2、固定blocksize,改变C值大小的实…
阅读更多...
104-127-linux-vim-shell基础

104-127-linux-vim-shell基础

104-linux-shell: 1.shell基础 分类&#xff1a;linux使用Bash&#xff0c;可通过vi /etc/shells查看linux支持的shell类型。 1、echo [rootlocalhost ~]#echo [选项] [输出内容] 选项:-e:支持反斜线控制的字符转换&#xff08;具体百度吧)-n:取消输出后行末的换行符号&…
阅读更多...
Python实现ALO蚁狮优化算法优化支持向量机分类模型(SVC算法)项目实战

Python实现ALO蚁狮优化算法优化支持向量机分类模型(SVC算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 蚁狮优化(Ant Lion Optimizer&#xff0c;ALO)算法是Mirjalili于2015提出的一种新型元启发式群智能算法…
阅读更多...
185.基于Django的富文本编辑器安装与使用

185.基于Django的富文本编辑器安装与使用

1.DjangoUeditor 1.1 概述 富文本编辑器&#xff0c;在web开发中必不可少&#xff0c;但是django没有自带富文本编辑器&#xff0c;因此我们需要使用第三方库&#xff0c;这里使用DjangoUeditor DjangoUditor是百度开源的在线HTML编辑器&#xff0c;功能非常强大&#xff0c;像…
阅读更多...
VUEElement简单介绍。

VUEElement简单介绍。

目录 一、VUE 1、基本介绍 2、Vue 指令 3、生命周期 二、Element 1、基本介绍 2、Element 布局 一、VUE 1、基本介绍 ▶ 概述 Vue 是一套前端框架&#xff0c;免除原生JavaScript中的DOM操作&#xff0c;简化书写。 我们之前也学习过后端的框架 Mybatis &#xff0c;My…
阅读更多...
Linux下C/C++实现类似netstat命令(列出TCP和UDP连接)

Linux下C/C++实现类似netstat命令(列出TCP和UDP连接)

网络连接一般包括最基本的五元组信息(源地址、目标地址、源端口、目标端口、协议号)再加上所属进程信息pid, exe, cmdline等。其中这两项数据大多可直接读取linux /proc目录下的网络状态连接文件/proc/net/tcp、/proc/net/udp), 进程状态目录(/proc/pid/xx)。 Linux 下的/proc…
阅读更多...
Java基于JSP的报刊订阅管理系统

Java基于JSP的报刊订阅管理系统

随着人类的发展&#xff0c;人们对信息的获取方式也越来越多&#xff0c;虽然很多时候人们习惯了通过手机来获取各类信息&#xff0c;但是手机也逐渐的成为了危害人类健康的杀手之一&#xff0c;为了能够让大家回归到健康的生活中来&#xff0c;我开发了本系统&#xff0c;旨在…
阅读更多...
基于jsp+mysql+ssm医药进销存管理系统-计算机毕业设计

基于jsp+mysql+ssm医药进销存管理系统-计算机毕业设计

项目介绍 为了减少传统医药进销存管理的繁杂的工作量&#xff0c;提高医药进销存管理的效率而设计开发了此系统。本系统综合各方面的需求决定采用B/S架构&#xff0c;并利用clipse搭建java开发平台。从而共同完成整个医药的设计开发。系统实现的功能主要包括&#xff1a;用户在…
阅读更多...
java 通过InetAddress获取ip 计算机名称操作

java 通过InetAddress获取ip 计算机名称操作

本文属于java网络编程部分 需要你的网络编程三要素 有所了解 如果您尚未了解 可以先查看我的文章 java网络编程三要素 而 为了更好的获取和使用IP地址 java提供了InetAddress类 来到文档 首先 他在 java的net包下 所以 想用它 是需要导包的 根据文档叙述 InetAddress就是一个…
阅读更多...
python数据分析及可视化（十七）聚宽（双均线分析、因子选股策略、多因子选股策略、均值回归理论、布林带策略、PEG策略、权重收益策略）

python数据分析及可视化（十七）聚宽（双均线分析、因子选股策略、多因子选股策略、均值回归理论、布林带策略、PEG策略、权重收益策略）

聚宽 聚宽是一个做金融量化的网站&#xff0c;https://www.joinquant.com&#xff0c;登录注册&#xff0c;如果你写的文章、策略被别人采纳&#xff0c;增加积分&#xff0c;积分用于免费的回测时长。在我的策略&#xff0c;进入策略列表&#xff0c;里面有做好的策略模板可以…
阅读更多...
Web前端105天-day40-GIT

Web前端105天-day40-GIT

git--版本控制系统(VCS) 目录 前言 一、版本控制系统(VCS) 二、Git中的常用概念 三、Git中的常用命令 四、分支 五、远程仓库(代码托管平台) 总结 前言 day40学习开始 一、版本控制系统(VCS) 用于项目中文件的存储、共享、历史回退、合并、代码追踪文件历史常用版本控制…
阅读更多...
acwing基础课——spfa

acwing基础课——spfa

由数据范围反推算法复杂度以及算法内容 - AcWing 常用代码模板3——搜索与图论 - AcWing 基本思想&#xff1a; 一般单源最短路我们都可以用spfa算法来做&#xff0c;如果过不了再尝试其他算法。 spfa算法就是在bellman-ford算法的基础上就行优化&#xff0c;bellman-算法是每…
阅读更多...
微信小程序|小程序事件

微信小程序|小程序事件

首先，我们在index.wxml中与index.js中添加如下代码： <button bindtap="alert">bindtap</button>Page({data: {},alert: function (event) {wx.showToast({title: 触发成功, // 标题icon: success, // 图标类型，默认successduration: 1500 // 提示窗停…
阅读更多...
贪吃蛇复现-CoCube

贪吃蛇复现-CoCube

需要完成下面所提及博文中里面所有前序案例&#xff1a; 从开环到闭环的旅程-CoCube 在完成如上代码之后&#xff0c;添加一个彩蛋&#xff0c;贪吃蛇的案例。 蓝桥ROS之半自动贪吃龟turtlesim版 基本上就是上述代码复现一下&#xff0c;完全没有难度的。 贪吃蛇复现-CoCubep…
阅读更多...
程序员最关心的问题，我都帮你们问AI了

程序员最关心的问题，我都帮你们问AI了

前言 最近几天互联网刮起了一阵ChatGPT风&#xff0c;起因是OpenAI发布了一个全新的聊天机器人模型—— ChatGPT&#xff0c;可以像人类交谈般回答大部分问题甚至还能直接帮你写代码。 我们先来试试让它帮我们写个代码&#xff1a; 有一丝丝的恐惧&#xff0c;害怕过两年就会失…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023