定义

一种可以实现“先进先出”的存储结构。并且只允许一端入，另一端为出。而且不能对中间的元素进项进行插入删除。栈是先进后出。且只允许在一端插入与删除，就是入口与出口都是同一个。

---

分类

链式队列

对链表进行一些操作和限制，就成了队列。
在栈当中，头部尾部的代号是Top和Bottom；队列当中，头部尾部的表达式是front和rear。

静态队列

用数组实现，定义头部与尾部之后，也可以实现队列，即把数组的一些功能砍掉，再增加一点队列的功能。静态队列都必须是循环队列。

循环队列

需要搞懂：

1. 静态队列为什么必须是循环队列？
2. 循环队列需要几个参数来确定？
3. 循环队列各个参数的含义。
4. 循环队列入队的伪代码。
5. 循环队列出队的伪代码。
6. 如何判断循环队列是否为空。
7. 如何判断循环队列是否已满。

---

如果f指向第一个元素，r指向最后一个的话，不好操作，参考链表，链表的第一个是头结点，里面是没有有效元素的。**则现在定义，front指向第一个有效元素的地址，而rear指向最后一个元素的下一个，**错开来，为了方便对队列进行操作。可以理解为两个指针其中有一个指向必须为空，如果首指针指向了一个有效节点，难么尾指针后移一位指，反之一样。

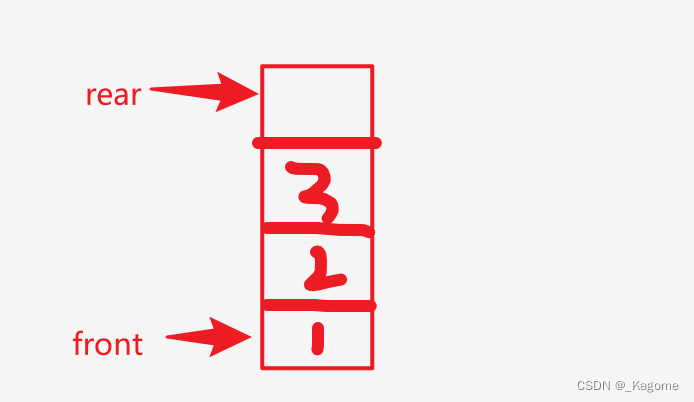
**front则是用来删除元素的，删除一个元素就往上移一个。**假如front从下往上删除元素，按照链表的思路来说，删除的元素删了，就有空间空闲出来了，但是静态队列不一样，这是基于数组的，数组删除元素后，空间成空闲空间了，无法填充继续使用，造成空间浪费。

**rear是添加元素的，每添加一个元素就网上移一个。**所以无论是删除还是添加，front与rear都往上移动，不论是入队还是出队，这两个参数都是只增不减。

静态队列为什么必须是循环队列？

上述静态队列当中增增删删，那么就会造成rear端溢出（但是CPP不会检查），而front端浪费，并且只能增不能减，造成空间的大量浪费。所以对于这种情况，可以采用循环队列的形式，即当rear已经指向数组最后一个元素时，**那么就可以转而将rear指向数组的第一个空出来的空间。**这就是使用循环队列。

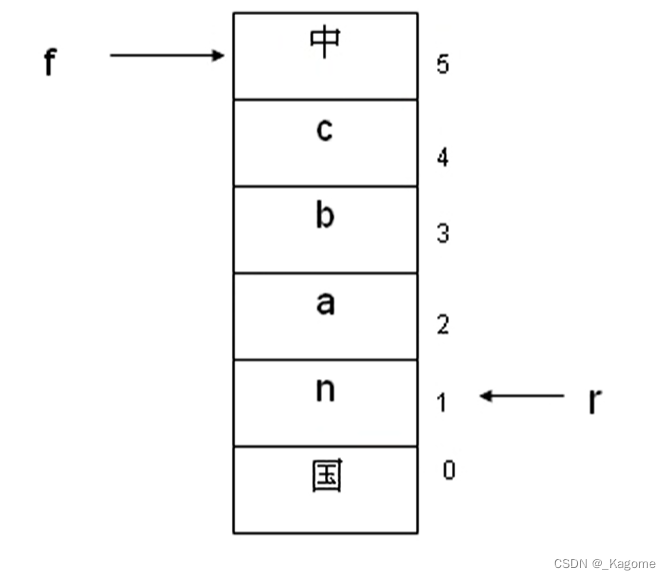
例如，这种就是循环队列，队列当中有“中 国”两个字符。

循环队列需要几个参数？

两个参数来确定，在不同场合（以下列举三个场合）有不同的含义。建议初学者先记住，再慢慢体会。

1. 初始化
   front和rear的值都是0
2. 队列非空
   front代表的是队列第一个元素
   rear代表的是队列最后一个有效元素
3. 队列空
   front和rear的值相等，但不一定是0

循环队列入队伪代码

具体步骤：

1. 将值存入当前rear所处的位置
2. 之后rear = (rear + 1) % length(数组)
   注意此处的错误写法是直接rear = rear + 1。

循环队列出队伪代码

具体步骤：

1. front = (front + 1) % length(数组)

判断循环队列是否为空

if (front == rear)

如果front和rear的值相等，那么该队列就是空的。

判断循环队列是否已满

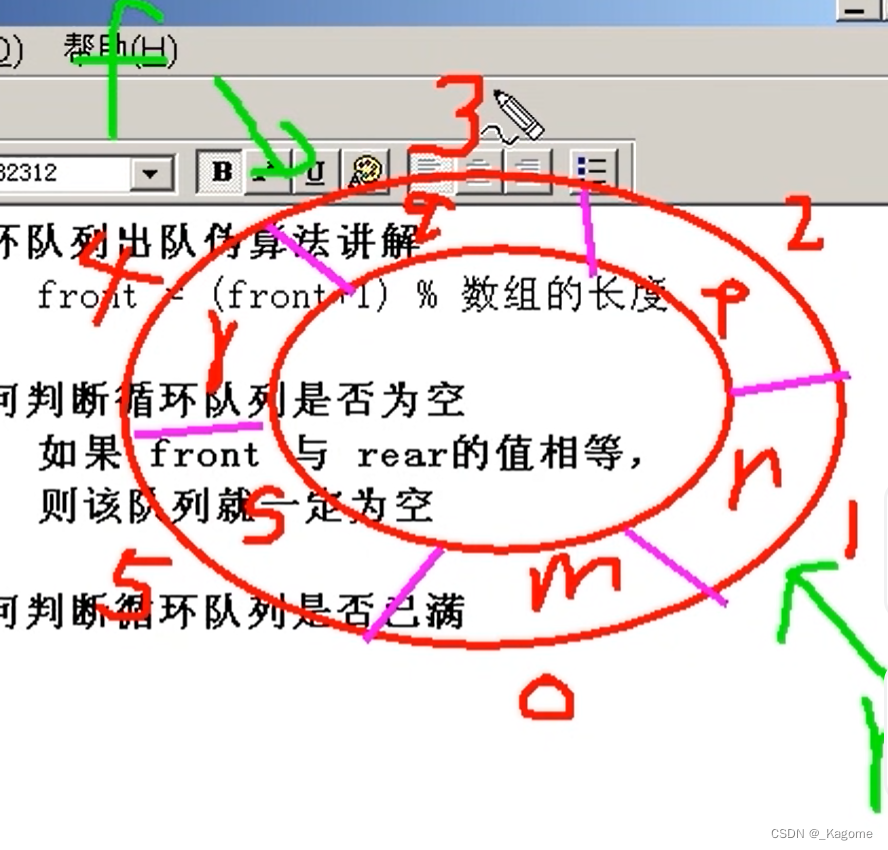
假如数的排布是这样的，现在front是指向了3号，rear是指向了1号，那么front的下一个元素应该指向哪里？是顺时针还是逆时针？参考以上的公式，front = (front + 1) % length(数组)，得出结论是4号元素即为front后面的那个元素。

需要注意的是，front与rear是没有规律的，front可以比rear大，这两个是没有任何规律的。

还有一个就是，当front == rear的时候，怎么判断是空了还是满了。

1. 使用循环队列的小妙招，假如队列只能放$n$个元素，现在最多放$n-1$个，剩下一个就空着，这样就好判断是否为满，是否为空。
2. 多增加一个标识参数。

以上方法常用方法1。用了方法1就使得上方判断队列为空的表达式正确且唯一了。

综上，如果rear和front紧挨着，则队列已满（空出一位）。

if ((r + 1) % (length(数组长度)) == f)
	return 满;
else
	return 不满;

循环队列的代码实现

#include <iostream>
#include <cmalloc>

using namespace std;

typedef struct Queue{
	int *pBase;
	int front;
	int rear;
}QUEUE;

void init(QUEUE *);
bool en_queue(QUEUE *, int val);
void traverse(QUEUE *);
bool full_queue(QUEUE *);
bool out_queue(QUEUE *, int *);
bool empty_queue(QUEUE *);

int main(){
	QUEUE Q;
	init(&Q);
	en_queue(&Q, 1);
	en_queue(&Q, 2);
	en_queue(&Q, 3);
	en_queue(&Q, 4);
	en_queue(&Q, 5);
	en_queue(&Q, 6);
	
	traverse(&Q);
	out_queue(&Q, &val);
	
	return 0;
} 

//初始化
void init(QUEUE *pQ)
{
	pQ->pBase = (int *)malloc(sizeof(int) * 6);
	pQ->front = 0;
	pQ->rear = 0;
}

//放值
bool en_queue(QUEUE *, int val)
{
	if (full_queue(pQ))
	{
		return false;
	}
	else
	{	pQ->pBase[pQ->rear] = val;
		pQ->rear = (pQ->rear + 1) % (6);
		return true;
	}
}

//判断是否已满
bool full_queue (QUEUE *pQ)
{
	if ((pQ->rear + 1) % 6 == pQ->front)
	{
		return true;
	}
	else
	{
		return false;
	}
}

void traverse(QUEUE *pQ)
{
	int i = pQ->front;
	while (i != pQ->rear)
	{
		cout << pQ->pBase[i] << endl;
		i = (i + 1) % 6;
	}
	return;
}

//出队
bool out_queue(QUEUE *, int *pVal)
{
	if (empty_queue(pQ))
		return false;
	else
	{
		*pVal = pQ->pBase[pQ->front];
		pQ->front = (pQ->front + 1) % 6;
		return true;
	}

}

//判断是否为空
bool empty_queue(QUEUE *pQ)
{
	if (pQ->front == pQ->rear)
		return true;
	else
	{
		return false;
	} 

}

队列的应用

所有和时间有关的操作都与队列有关。