二叉树的链式结构 - 遍历

前序、中序以及后序遍历

二叉树遍历 (Traversal) 是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

按照规则，二叉树的遍历有：前序/中序/后序 的递归结构遍历 ：

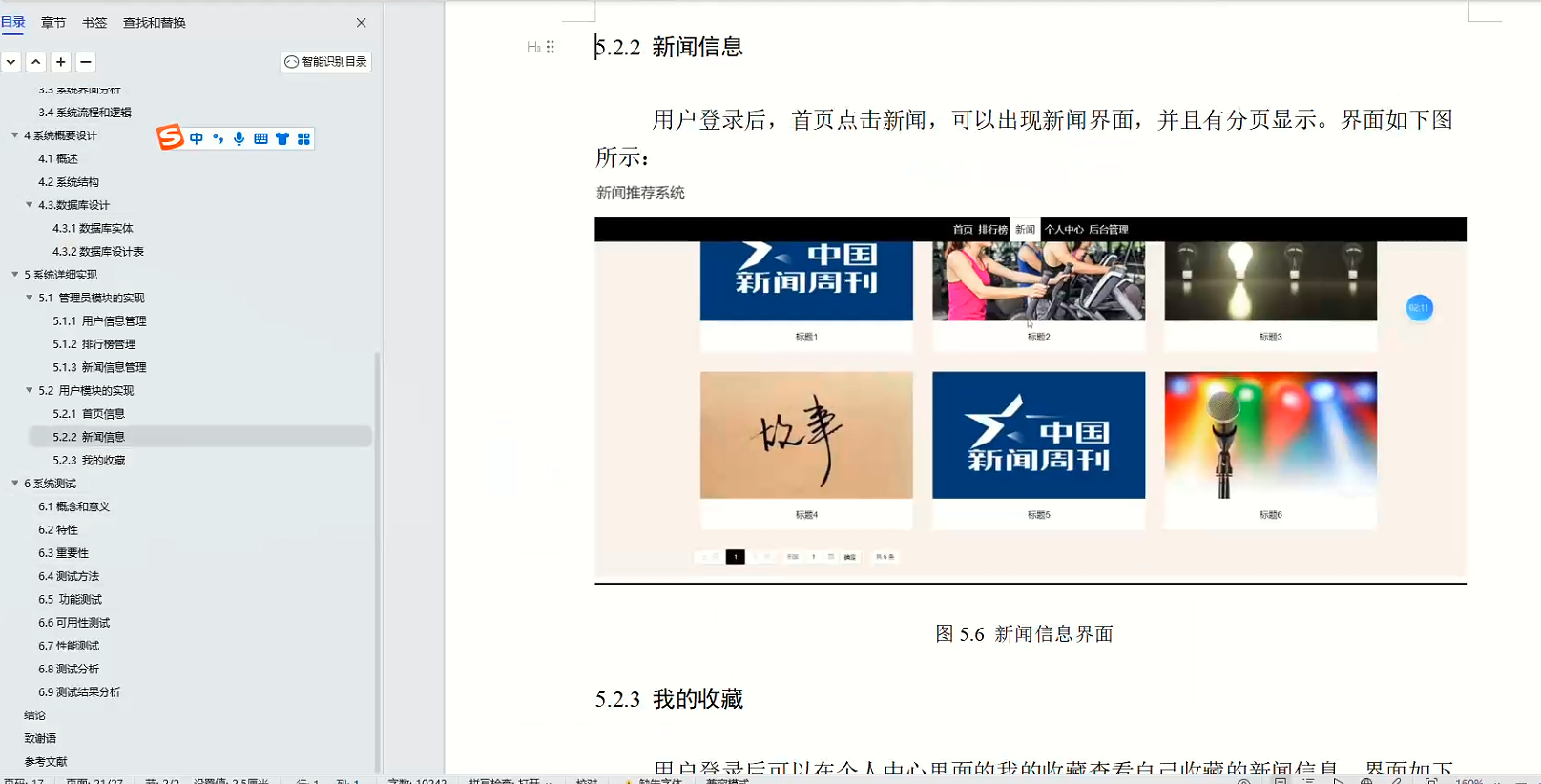
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以 N(Node ）、 L(Left subtree ）和 R(Right subtree ）又可解释为 根、根的左子树和根的右子树 。 NLR 、 LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历。

// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);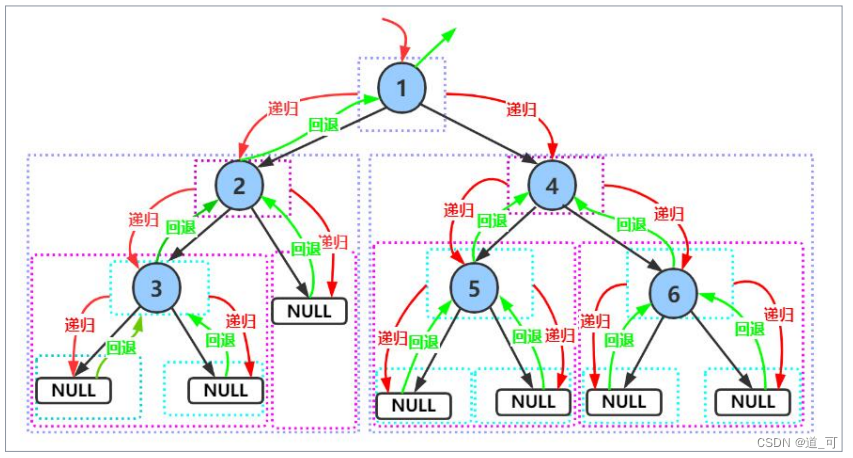

前序遍历递归图解 ：

//.........................................以上概念性内容均来自比特科技..........................................................

为了更直观的了解，首先手搓一颗二叉树

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;


BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	assert(node);

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

其次，我们使用前/中/后序来访问一下：

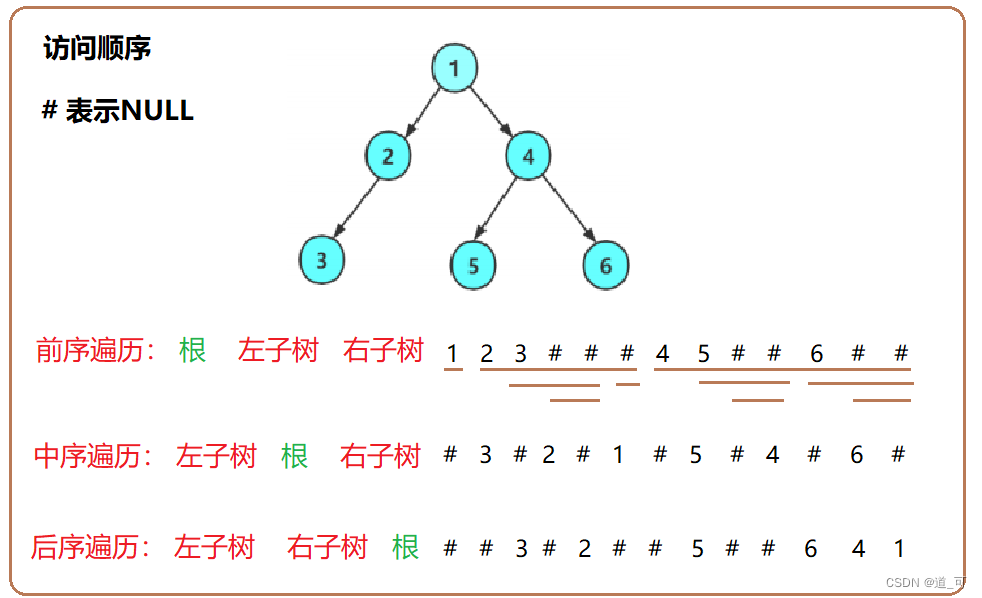
代码实现：

前序：

//前序
void PreOrder(BTNode* root){
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

中序：

//中序
void InOrder(BTNode* root){
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

后序：

//后序
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

变形

思路：分治算法，分而治之，把大问题转换成类似规模的小问题。（一般采用递归）

1.求二叉树结点的个数

这里有两种方法，①是定义一个全局变量，每递归一次，变量就++一次。

②是先求出左子树结点的个数再加上右子树结点的个数，最后再加上根。因为是递归，所以一直可以向下分割成左右子树，直到遇见NULL树，才不再分割。以下例题，多数都是这种思想。

//求二叉树结点的个数

int count = 0;
int TreeSize1(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	count++;//注：这里需要定义全局变量，因为是递归，所以不能使用局部变量

	TreeSize1(root->left);
	TreeSize1(root->right);
}

int TreeSize2(BTNode* root)
{
	return root == NULL ? 0 :
		TreeSize2(root->left) + TreeSize2(root->right) + 1;
	
	//if (root == NULL)
	//{
	//	return 0;
	//}
	//else
	//{
	//	TreeSize2(root->left) + TreeSize2(root->right) + 1;
	//}

}

2.求叶子结点的个数

思路：也是两种方法，第一种方法是在上一道例题的基础上，创建一个全局变量，用if判断。

第二种方法就是求出左树和右树的叶子结点然后相加。

//求叶子结点的个数
int TreeLeafSize1(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	if (root->left == NULL && root->right == NULL)
	{
		count++;//定义一个全局变量
	}

	TreeLeafSize1(root->left);
	TreeLeafSize1(root->right);
	
}

//方法2
int TreeLeafSize2(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return TreeLeafSize2(root->left) + TreeLeafSize2(root->right);
}

3.求第k层结点的个数

思路：转换成子问题，求左子树的k-1层+右子树的k-1层

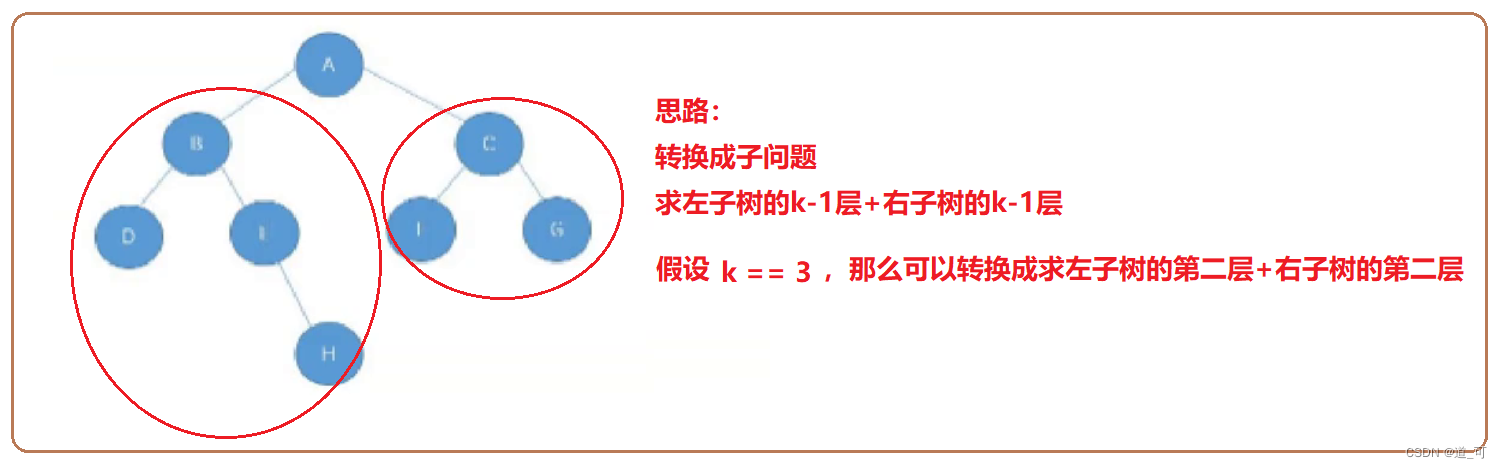
//求第k层结点的个数
int TreeKLevel(BTNode* root, int k){
	assert(k >= 1);
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return TreeKLevel(root->left, k - 1) +
		TreeKLevel(root->right, k - 1);
}

4.求二叉树的深度

思路：求出左树的深度，再求出右树的深度，加1是加根，然后比较以下，谁大/深返回谁。

//求二叉树的深度
int TreeDepth(BTNode* root)
{
	if (root == NULL)
		return NULL;

	int leftDepth = TreeDepth(root->left)+1;
	int rightDepth = TreeDepth(root->right)+1;

	return leftDepth > rightDepth ? leftDepth  : rightDepth ;
}

5.二叉树中查找值为x结点的值

注：这里值得注意的一点是，返回值的问题以及跳出递归。用前序遍历一下就行。

//二叉树中查找值为x结点的值
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;

	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1) //这里的条件是ret1不为空
		return ret1;

	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;

	return NULL;
}

oj练习 - C语言解题

1. 单值二叉树。 Oj链接

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
         return true;
    
    if(root->left && root->left->val != root->val)
        return false;

     if(root->right && root->right->val != root->val)
          return false;
     
   return  isUnivalTree(root->left)&&
     isUnivalTree(root->right);
    //同时为true 才为true
    //一个为false 就返回false

    //根  和左孩子右孩子比较，如果不相同，就return false
    //如果相同，就继续向下看左子树，再看右子树
    //左子树继续向下划分根 左孩子 右孩子

}

2. 检查两颗树是否相同。 OJ链接

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if( p == NULL && q == NULL)//同时为空
          return true;
    
    if(p == NULL  ||  q == NULL)//走到这里必定有一个为空，一个不为空
          return false;

    if(p->val != q->val )
       return false;

    return  isSameTree(p->left,q->left)//左子树跟左子树比较
     && isSameTree(p->right,q->right);//右子树跟右子树比较
 
}

3. 对称二叉树。 OJ链接

bool isSymmetricSubTree(struct TreeNode* root1,struct TreeNode* root2)
{
    if(root1 == NULL && root2 == NULL)
        return true;

    if(root1 == NULL || root2 == NULL)//走到这里必定一个为空一个不为空
       return false;
    
    if(root1->val != root2->val)//必定同时不为空，比较val值
        return false;
    
    return isSymmetricSubTree(root1->left,root2->right)
    &&isSymmetricSubTree(root1->right,root2->left);
    //左树的左孩子比较右树的右孩子
    //左树的右孩子比较右树的左孩子
}

bool isSymmetric(struct TreeNode* root){
    
    if(root == NULL)
       return true;

    //以根为分割线 -- 镜像二叉树
    
    return isSymmetricSubTree(root->left,root->right);
    //根的左孩子右孩子传过去
}

4. 二叉树的前序遍历。 OJ链接

//注意：返回的值必须要放进malloc申请的数组空间里面
 //returnSize ：默认不给空间大小，也就是我们需要求出数组的大小

//首先求出malloc数组空间的大小
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left)+TreeSize(root->right)+1;
}

//这里为什么i需要传地址，因为我们需要的是一个i 而不是栈帧空间中的每一个独立的i
//因为下面子树改变i，不会影响上面根的i，这就导致数据可能会重叠，导致后面的空间出现随机数
void prevorder(struct TreeNode* root,int* arr,int* i)
{
    if(root == NULL)
        return;

    arr[(*i)++] = root->val;

    prevorder(root->left,arr,i);
    prevorder(root->right,arr,i);

}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    
    *returnSize = TreeSize(root);

    int* arr = (int*)malloc(*returnSize * sizeof(int));

    int i = 0;//数组下标
    prevorder(root,arr,&i);
 
    return arr;

}

5. 另一颗树的子树。 OJ链接

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if( p == NULL && q == NULL)//同时为空
          return true;
    
    if(p == NULL  ||  q == NULL)//走到这里必定有一个为空，一个不为空
          return false;

    if(p->val != q->val )
       return false;

    return  isSameTree(p->left,q->left)//左子树跟左子树比较
     && isSameTree(p->right,q->right);//右子树跟右子树比较
 
}

 //思路：把原树中的所有子树都找出来与subRoot进行比较
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){

   if(root == NULL)
      return false;


    //遍历所有子树进行比较 ，subroot与root所有的根节点进行比较
    if(isSameTree(root,subRoot))
        return true;
   
    //角度2.
    //先与当前树进行比较，如果不是当前树的子树
    //那么就去与当前树的左子树进行比较
    //如果也不是
    //就与当前树的右子树进行比较
    //只要有一个为true 就可以，所有这里是或|| 
    return isSubtree(root->left,subRoot)
            || isSubtree(root->right,subRoot);

}

6.二叉树的构建及遍历 。 OJ链接

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>


typedef char BTDataType;
typedef struct BinaryTreeNode {
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
    BTDataType data;
} BTNode;


BTNode* BuyNode(BTDataType x) {
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    assert(node);

    node->data = x;
    node->left = NULL;
    node->right = NULL;

    return node;
}

BTNode* CreateTree(char* arr,int* i)//前序构建
{
    if(arr[*i] == '#')
    {
        (*i)++;
        return NULL;
    }

    BTNode* root = BuyNode(arr[(*i)++] );

    root->left = CreateTree(arr,i);//先构建左子树
    root->right = CreateTree(arr,i);//再构建右子树

    return root;//返回根节点
}

//中序遍历
void Inorder(BTNode* root)
{
    if(root == NULL)
        return ;

    Inorder(root->left);
    printf("%c ",root->data);
    Inorder(root->right);

}

int main()
{
    char arr[100]={0};
    scanf("%s",arr);

    int i=0;//数组下标
    BTNode* root = CreateTree(arr,&i);
    Inorder(root);

    return 0;
}

以上仅供参考