一：题目描述：

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

二：示例与提示

示例 1:

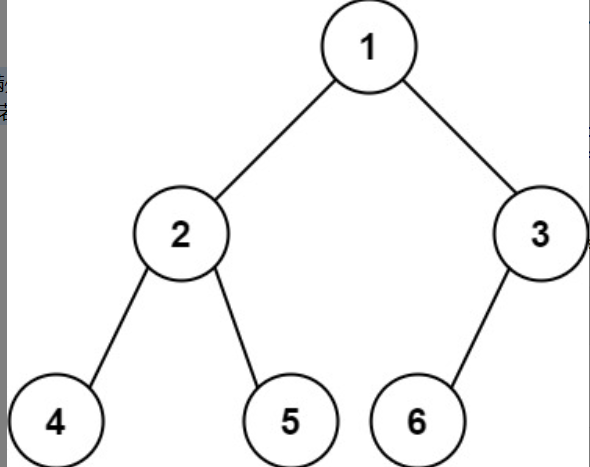
输入：root = [1,2,3,4,5,6]
输出：6

示例 2:

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示:

• 树中节点的数目范围是[0, 5 * 104]
• 0 <= Node.val <= 5 * 104
• 题目数据保证输入的树是 完全二叉树

---

三：思路

正常遍历求节点个数

• 使用层次遍历，遍历每一层元素个数求和即可

使用完全二叉树特性和满二叉树节点个数计算公式

• 完全二叉树，除最后一层可以没有达到满节点，其余节点都是填满整层的
• 满二叉树节点个数为2 ^ n - 1，n为该节点的深度
• 那就先判断子树是否为满二叉树，如果是满二叉树可以直接利用公式，通过判断左外侧和右外侧的深度是否相等即可判断是否为满二叉树
• 如果不是满二叉树，返回父节点左子树的节点个数和右子树节点个数 + 1即可

四：代码

层序遍历求节点个数

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function(root) {
    //层序遍历
    let res = 0
    if(!root) return res
    //队列
    let queue = [root]
    while(queue.length){
        //记录队列的长度
        let length = queue.length
        //记录每一层的临时一维数组
        let curLevel = []
        for(let i = 0; i < length; i++){
            //出队
            let node = queue.shift()
            curLevel.push(node.val)
            //若存在左右子节点入队
            if(node.left) queue.push(node.left)
            if(node.right) queue.push(node.right)

        }
        res += curLevel.length
    }
    return res
};

完全二叉树特性

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function(root) {
    //完全二叉树解法 节点为2^n - 1 n为深度
    if(!root) return 0
    //终止条件
    let leftDepth = 1
    let rightDepth = 1
    //
    let leftNode = root.left
    let rightNode = root.right
    while(leftNode){
        //不断遍历左节点 直到为空
        leftNode = leftNode.left
        //左侧深度++
        leftDepth++
    }
    while(rightNode){
        rightNode = rightNode.right
        rightDepth++
    }
    //判断是否该节点下的子树是否为满二叉树
    if(leftDepth === rightDepth){
        return Math.pow(2, leftDepth) - 1
    }
    //左
    let leftNumber = countNodes(root.left)
    //右
    let rightNumber = countNodes(root.right)
    //中
    return leftNumber + rightNumber + 1
};