欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
参考自polygon mesh proccessing这本书
重心坐标定理
定理证明点击前往
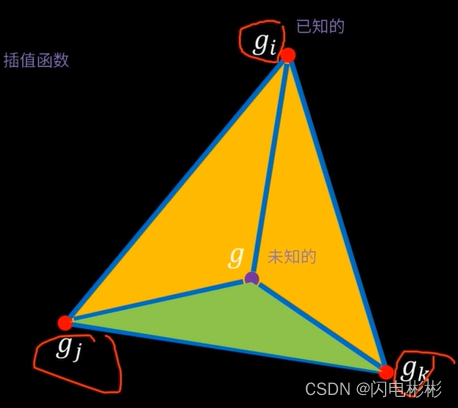
已经三角形三点上的函数值分别为gi,gj,gk。
可以利用插值得到g处的函数值。
g
=
α
g
i
+
β
g
j
+
γ
g
k
g=\alpha g_i+\beta g_j+ \gamma g_k
g=αgi+βgj+γgk
α
+
β
+
γ
=
1
,
\alpha + \beta + \gamma = 1,
α+β+γ=1,
α
,
β
,
γ
>
0
\alpha,\beta,\gamma>0
α,β,γ>0
α
=
s
i
s
i
+
s
j
+
s
k
\alpha = \frac {s_i} {s_i+s_j+s_k}
α=si+sj+sksi
β
=
s
j
s
i
+
s
j
+
s
k
\beta = \frac {s_j} {s_i+s_j+s_k}
β=si+sj+sksj
γ
=
s
k
s
i
+
s
j
+
s
k
\gamma = \frac {s_k} {s_i+s_j+s_k}
γ=si+sj+sksk
s i 是 g i 对面与 g 组成的小三角形, s j , s k 类似 s_i 是g_i对面与g组成的小三角形,s_j, s_k类似 si是gi对面与g组成的小三角形,sj,sk类似
函数定义
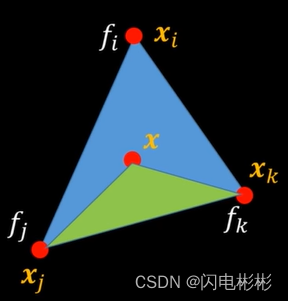
利用上述原理,x处的函数值
f
(
x
)
=
α
f
i
+
β
f
j
+
γ
f
k
f(x) = \alpha f_i+\beta f_j + \gamma f_k
f(x)=αfi+βfj+γfk
梯度定义
梯度是对函数进行求导, f i , f j , f k 是已知量,只要对 α , β , γ 求导即可。 梯度是对函数进行求导,f_i,f_j,f_k 是已知量,只要对\alpha, \beta, \gamma求导即可。 梯度是对函数进行求导,fi,fj,fk是已知量,只要对α,β,γ求导即可。
∇ x f ( x ) = f i ∇ x α + f j ∇ x β + f k ∇ x γ \nabla_xf(x)=f_i\nabla_x\alpha+f_j\nabla_x\beta+f_k\nabla_x\gamma ∇xf(x)=fi∇xα+fj∇xβ+fk∇xγ
梯度求解
利用三角形面积底高公式
以 α 为例,对于 A i 面积,底是 ∥ x k − x j ∥ 2 , 高是向量 ( x − x j ) 在 ( x k − x j ) 垂直方向上的投影 以\alpha为例,对于A_i面积,底是\|x_k-x_j\|_2, 高是向量(x-x_j)在(x_k-x_j)垂直方向上的投影 以α为例,对于Ai面积,底是∥xk−xj∥2,高是向量(x−xj)在(xk−xj)垂直方向上的投影
α
=
A
i
A
T
=
(
(
x
−
x
j
)
⋅
(
x
k
−
x
j
)
⊥
∥
x
k
−
x
j
∥
2
)
⋅
∥
x
k
−
x
j
∥
2
2
A
T
\alpha = \frac {A_i}{A_T}=\frac {\left( (x-x_j)\cdot \frac {(x_k-x_j)^\perp}{\|x_k-x_j\|_2}\right) \cdot\|x_k-x_j\|_2}{2A_T}
α=ATAi=2AT((x−xj)⋅∥xk−xj∥2(xk−xj)⊥)⋅∥xk−xj∥2
=
(
x
−
x
j
)
⋅
(
x
k
−
x
j
)
⊥
2
A
T
=\frac { (x-x_j)\cdot (x_k-x_j)^\perp }{2A_T}
=2AT(x−xj)⋅(xk−xj)⊥
上式中变量只有x, 求导如下
∇
x
α
=
(
x
k
−
x
j
)
⊥
2
A
T
\nabla_x\alpha = \frac { (x_k-x_j)^\perp }{2A_T}
∇xα=2AT(xk−xj)⊥
∇
x
β
=
(
x
i
−
x
k
)
⊥
2
A
T
\nabla_x\beta= \frac { (x_i-x_k)^\perp }{2A_T}
∇xβ=2AT(xi−xk)⊥
∇
x
γ
=
(
x
j
−
x
i
)
⊥
2
A
T
\nabla_x\gamma = \frac { (x_j-x_i)^\perp }{2A_T}
∇xγ=2AT(xj−xi)⊥
致此,梯度已经得到
∇ x f ( x ) = f i ( x k − x j ) ⊥ 2 A T + f j ( x i − x k ) ⊥ 2 A T + f k ( x j − x i ) ⊥ 2 A T \nabla_xf(x)=f_i\frac { (x_k-x_j)^\perp }{2A_T}+f_j \frac { (x_i-x_k)^\perp }{2A_T}+f_k\frac { (x_j-x_i)^\perp }{2A_T} ∇xf(x)=fi2AT(xk−xj)⊥+fj2AT(xi−xk)⊥+fk2AT(xj−xi)⊥
公式化简
三角形三条边为向量走一遍最后回到起点,可以得到
( x k − x j ) + ( x i − x k ) + ( x j − x i ) = 0 (x_k-x_j)+(x_i-x_k)+(x_j-x_i)=0 (xk−xj)+(xi−xk)+(xj−xi)=0
把所有向量转90度再相加,结果不变。
( x k − x j ) ⊥ + ( x i − x k ) ⊥ + ( x j − x i ) ⊥ = 0 (x_k-x_j)^\perp+(x_i-x_k)^\perp+(x_j-x_i)^\perp=0 (xk−xj)⊥+(xi−xk)⊥+(xj−xi)⊥=0
将梯度公式中xk-xj替换得到
∇ x f ( x ) = ( f j − f i ) ( x i − x k ) ⊥ 2 A T + ( f k − f i ) ( x j − x i ) ⊥ 2 A T \nabla_xf(x)=(f_j-f_i) \frac { (x_i-x_k)^\perp }{2A_T}+(f_k-f_i)\frac { (x_j-x_i)^\perp }{2A_T} ∇xf(x)=(fj−fi)2AT(xi−xk)⊥+(fk−fi)2AT(xj−xi)⊥
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。