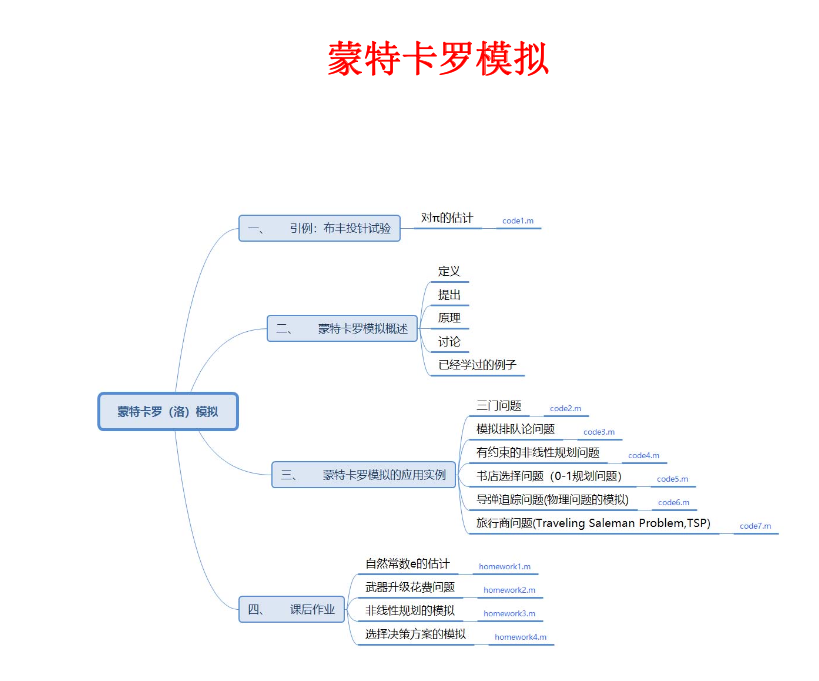


%% 蒙特卡罗用于模拟三门问题
clear;clc
%% (1)预备知识
% randi([a,b],m,n)函数可在指定区间[a,b]内随机取出大小为m*n的整数矩阵
randi([1,5],5,8) %在区间[1,5]内随机取出大小为5*8的整数矩阵
% 2 5 4 5 3 1 4 2
% 3 3 1 5 4 2 1 2
% 4 1 3 3 2 2 5 1
% 5 3 3 4 4 5 4 4
% 4 2 3 4 2 4 2 4
randi([1,5]) %在区间[1,5]内随机取出1个整数
% 3
% 字符串的连接方式:(1)['字符串1','字符串2'] (2)strcat('字符串1','字符串2') (第一期视频第一讲)
['数学建模','学习交流']
strcat('数学建模','学习交流')
% num2str函数:将数值转换为字符串 (第一期视频第一讲)
mystr = num2str(1224) % 注意观察工作区的mystr这个变量的值
disp([num2str(1224),'祝大家平安夜平平安安']) % disp函数是输出函数
%% (2)代码部分(在成功的条件下的概率)
n = 100000; % n代表蒙特卡罗模拟重复次数
a = 0; % a表示不改变主意时能赢得汽车的次数
b = 0; % b表示改变主意时能赢得汽车的次数
for i= 1 : n % 开始模拟n次
x = randi([1,3]); % 随机生成一个1-3之间的整数x表示汽车出现在第x扇门后
y = randi([1,3]); % 随机生成一个1-3之间的整数y表示自己选的门
% 下面分为两种情况讨论:x=y和x~=y
if x == y % 如果x和y相同,那么我们只有不改变主意时才能赢
a = a + 1; b = b + 0;
else % x ~= y ,如果x和y不同,那么我们只有改变主意时才能赢
a = a + 0; b = b +1;
end
end
disp(['蒙特卡罗方法得到的不改变主意时的获奖概率为:', num2str(a/n)]);
disp(['蒙特卡罗方法得到的改变主意时的获奖概率为:', num2str(b/n)]);
%% (3)考虑失败情况的代码(无条件概率)
n = 100000; % n代表蒙特卡罗模拟重复次数
a = 0; % a表示不改变主意时能赢得汽车的次数
b = 0; % b表示改变主意时能赢得汽车的次数
c = 0; % c表示没有获奖的次数
for i= 1 : n % 开始模拟n次
x = randi([1,3]); % 随机生成一个1-3之间的整数x表示汽车出现在第x扇门后
y = randi([1,3]); % 随机生成一个1-3之间的整数y表示自己选的门
change = randi([0, 1]); % change =0 不改变主意,change = 1 改变主意
% 下面分为两种情况讨论:x=y和x~=y
if x == y % 如果x和y相同,那么我们只有不改变主意时才能赢
if change == 0 % 不改变主意
a = a + 1;
else % 改变了主意
c= c+1;
end
else % x ~= y ,如果x和y不同,那么我们只有改变主意时才能赢
if change == 0 % 不改变主意
c = c + 1;
else % 改变了主意
b= b + 1;
end
end
end
disp(['蒙特卡罗方法得到的不改变主意时的获奖概率为:', num2str(a/n)]);
disp(['蒙特卡罗方法得到的改变主意时的获奖概率为:', num2str(b/n)]);
disp(['蒙特卡罗方法得到的没有获奖的概率为:', num2str(c/n)]);
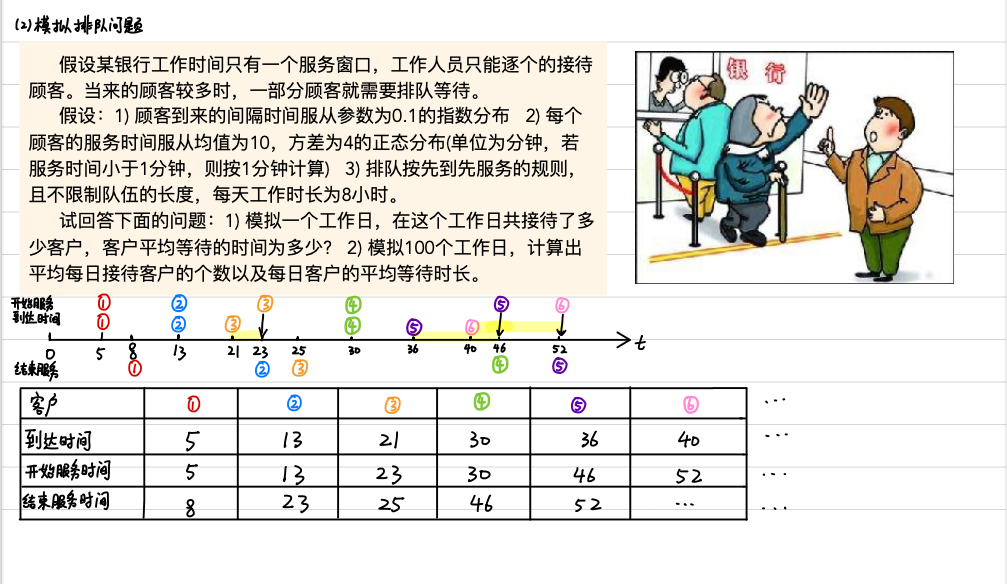
%% 蒙特卡罗模拟排队问题
%% (1)预备知识
% normrnd(MU,SIGMA):生成一个服从正态分布(MU参数代表均值,SIGMA参数代表标准差,方差开根号是标准差)的随机数
normrnd(10,2) % 均值为10 标准差为2(方差为4)的正态分布随机数
% exprnd(M)表示生成一个均值为M的指数分布随机数(其对应的参数为1/M)
exprnd(5) % 均值为5的指数分布随机数(对应的参数为0.2)
% mean函数是用来求解均值的函数(第一期视频第五讲)
mean([1,2,3])
% tic函数和toc函数可以用来返回代码运行的时间,例如我们要计算一段代码的运行时间,就可以在这段代码前加上tic,在这段代码后加上toc (我的微信公众号"数学建模学习交流"中有一篇推送《为什么要对代码初始化》中使用过这对函数)
tic
a = 2^100
toc
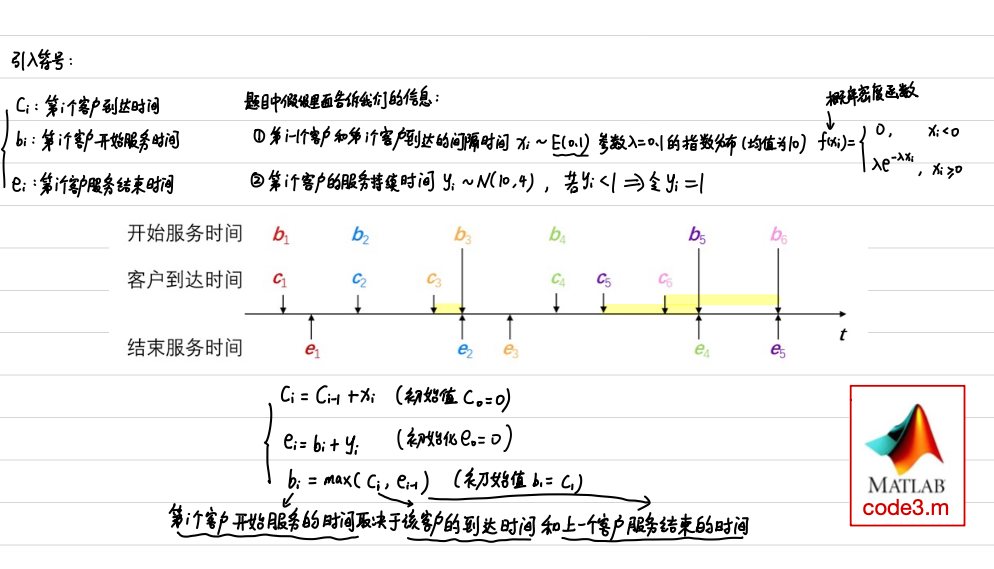
%% (2)模型中出现的变量的说明
% x(i)表示第i-1个客户和第i个客户到达的间隔时间,服从参数为0.1的指数分布
% y(i)表示第i个客户的服务持续时间,服从均值为10方差为4(标准差为2)的正态分布 (若小于1则按1计算)
% c(i)表示第i个客户的到达时间,那么c(i) = c(i-1) + x(i),初始值c0=0
% b(i)表示第i个客户开始服务的时间
% e(i)表示第i个客户结束服务的时间,初始值e0=0
% 第i个客户结束服务的时间 = 第i个客户开始服务的时间 + 第i个客户的服务持续时间
% 即:e(i) = b(i) + y(i)
% 第i个客户开始服务的时间取决于该客户的到达时间和上一个客户结束服务的时间
% 即:b(i) = max(c(i),e(i-1)),初始值b1=c1;
% 第i个客户等待的时间 = 第i个客户开始服务的时间 - 第i个客户到达银行的时间
% 即:wait(i) = b(i) - c(i)
% w表示所有客户等待时间的总和
% 假设一天内银行最终服务了n个顾客,那么客户的平均等待时间t = w/n
%% (3)问题1的代码
clear
tic %计算tic和toc中间部分的代码的运行时间
i = 1; % i表示第i个客户,最开始取i=1
w = 0; % w用来表示所有客户等待的总时间,初始化为0
e0 = 0; c0 = 0; % 初始化e0和c0为0
x(1) = exprnd(10); % 第0个客户(假想的)和第1个客户到达的时间间隔
c(1) = c0 + x(1); % 第1个客户到达的时间
b(1) = c(1); % 第1个客户的开始服务的时间
while b(i) <= 480 % 开始设置循环,只要第i个顾客开始服务的时间(时刻)小于480,就可以对其服务(银行每天工作8小时,折换为分钟就是480分钟)
y(i) = normrnd(10,2); % 第i个客户的服务持续时间,服从均值为10方差为4(标准差为2)的正态分布
if y(i) < 1 % 根据题目的意思:若服务持续时间不足一分钟,则按照一分钟计算
y(i) = 1;
end
e(i) = b(i) + y(i); % 第i个客户结束服务的时间 = 第i个客户开始服务的时间 + 第i个客户的服务持续时间
wait(i) = b(i) - c(i); % 第i个客户等待的时间 = 第i个客户开始服务的时间 - 第i个客户到达银行的时间
w = w + wait(i); % 更新所有客户等待的总时间
i = i + 1; % 增加一名新的客户
x(i) = exprnd(10); % 这位新客户和上一个客户到达的时间间隔
c(i) = c(i-1) + x(i); % 这位新客户到达银行的时间 = 上一个客户到达银行的时间 + 这位新客户和上一个客户到达的时间间隔
b(i) = max(c(i),e(i-1)); % 这个新客户开始服务的时间取决于其到达时间和上一个客户结束服务的时间
end
n = i-1; % n表示银行一天8小时一共服务的客户人数
t = w/n; % 客户的平均等待时间
disp(['银行一天8小时一共服务的客户人数为: ',num2str(n)])
disp(['客户的平均等待时间为: ',num2str(t)])
toc %计算tic和toc中间部分的代码的运行时间
%% (4)问题2的代码
clear
tic %计算tic和toc中间部分的代码的运行时间
day = 100; % 假设模拟100天
n = zeros(day,1); % 初始化用来保存每日接待客户数结果的矩阵
t = zeros(day,1); % 初始化用来保存每日客户平均等待时长的矩阵
for k = 1:day
i = 1; % i表示第i个客户,最开始取i=1
w = 0; % w用来表示所有客户等待的总时间,初始化为0
e0 = 0; c0 = 0; % 初始化e0和c0为0
x(1) = exprnd(10); % 第0个客户(假想的)和第1个客户到达的时间间隔
c(1) = c0 + x(1); % 第1个客户到达的时间
b(1) = c(1); % 第1个客户的开始服务的时间
while b(i) <= 480 % 开始设置循环,只要第i个顾客开始服务的时间(时刻)小于480,就可以对其服务(银行每天工作8小时,折换为分钟就是480分钟)
y(i) = normrnd(10,2); % 第i个客户的服务持续时间,服从均值为10方差为4(标准差为2)的正态分布
if y(i) < 1 % 根据题目的意思:若服务持续时间不足一分钟,则按照一分钟计算
y(i) = 1;
end
e(i) = b(i) + y(i); % 第i个客户结束服务的时间 = 第i个客户开始服务的时间 + 第i个客户的服务持续时间
wait(i) = b(i) - c(i); % 第i个客户等待的时间 = 第i个客户开始服务的时间 - 第i个客户到达银行的时间
w = w + wait(i); % 更新所有客户等待的总时间
i = i + 1; % 增加一名新的客户
x(i) = exprnd(10); % 这位新客户和上一个客户到达的时间间隔
c(i) = c(i-1) + x(i); % 这位新客户到达银行的时间 = 上一个客户到达银行的时间 + 这位新客户和上一个客户到达的时间间隔
b(i) = max(c(i),e(i-1)); % 这个新客户开始服务的时间取决于其到达时间和上一个客户结束服务的时间
end
n(k) = i-1; % n(k)表示银行第k天服务的客户人数
t(k) = w/n(k); % t(k)表示该银行第k天客户的平均等待时间
end
disp([num2str(day),'个工作日中,银行每日平均服务的客户人数为: ',num2str(mean(n))])
disp([num2str(day),'个工作日中,银行每日客户的平均等待时间为: ',num2str(mean(t))])
toc %计算tic和toc中间部分的代码的运行时间

%% 蒙特卡罗求解有约束的非线性规划问题
% max f(x) = x1*x2*x3
% s.t.
% (1) -x1+2*x2+2*x3>=0
% (2) x1+2*x2+2*x3<=72
% (3) x2<=20 & x2>=10
% (4) x1-x2 == 10
%% (1)预备知识
% (1) format long g 可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
5/7
5895*514100
format long g
5/7
5895*514100
% (2)unifrnd(a,b,m,n)可以输出在[a,b]之间均匀分布的随机数组成的m行n列的矩阵。(等价于 a + rand(m,n)*(b-a))
unifrnd(0,5,4,3)
% 4.07361843196589 3.16179623112705 4.78753417717149
% 4.5289596853781 0.487702024997048 4.82444267599638
% 0.63493408146753 1.39249109433524 0.788065408387741
% 4.5668792806951 2.73440759602492 4.85296390880308
%% (2)代码部分
clc,clear;
tic %计算tic和toc中间部分的代码的运行时间
n=10000000; %生成的随机数组数
x1=unifrnd(20,30,n,1); % 生成在[20,30]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=x1 - 10;
x3=unifrnd(-10,16,n,1); % 生成在[-10,16]之间均匀分布的随机数组成的n行1列的向量构成x3
fmax=-inf; % 初始化函数f的最大值为负无穷(后续只要找到一个比它大的我们就对其更新)
for i=1:n
x = [x1(i), x2(i), x3(i)]; %构造x向量, 这里千万别写成了:x =[x1, x2, x3]
if (-x(1)+2*x(2)+2*x(3)>=0) & (x(1)+2*x(2)+2*x(3)<=72) % 判断是否满足条件
result = x(1)*x(2)*x(3); % 如果满足条件就计算函数值
if result > fmax % 如果这个函数值大于我们之前计算出来的最大值
fmax = result; % 那么就更新这个函数值为新的最大值
X = x; % 并且将此时的x1 x2 x3保存到一个变量中
end
end
end
disp(strcat('蒙特卡罗模拟得到的最大值为',num2str(fmax)))
disp('最大值处x1 x2 x3的取值为:')
disp(X)
toc %计算tic和toc中间部分的代码的运行时间
%% (3)缩小范围重新模拟得到更加精确的取值
clc,clear;
tic %计算tic和toc中间部分的代码的运行时间
n=10000000; %生成的随机数组数
x1=unifrnd(22,23,n,1); % 生成在[22,23]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=x1 - 10;
x3=unifrnd(11,13,n,1); % 生成在[11,13]之间均匀分布的随机数组成的n行1列的向量构成x3
fmax=-inf; % 初始化函数f的最大值为负无穷(后续只要找到一个比它大的我们就对其更新)
for i=1:n
x = [x1(i), x2(i), x3(i)]; %构造x向量, 这里千万别写成了:x =[x1, x2, x3]
if (-x(1)+2*x(2)+2*x(3)>=0) & (x(1)+2*x(2)+2*x(3)<=72) % 判断是否满足条件
result = x(1)*x(2)*x(3); % 如果满足条件就计算函数值
if result > fmax % 如果这个函数值大于我们之前计算出来的最大值
fmax = result; % 那么就更新这个函数值为新的最大值
X = x; % 并且将此时的x1 x2 x3保存到一个变量中
end
end
end
disp(strcat('蒙特卡罗模拟得到的最大值为',num2str(fmax)))
disp('最大值处x1 x2 x3的取值为:')
disp(X)
toc %计算tic和toc中间部分的代码的运行时间
%% 书店买书问题的蒙特卡罗的模拟
%% (1)预备知识
% (1)unique函数: 剔除一个矩阵或者向量的重复值,并将结果按照从小到大的顺序排列
% adj. 唯一的; 独一无二的 [ju'ni:k]
unique([1 2 5; 6 8 9;2 4 6])
unique([5 6 8 8 4 1 6 2 2 4 8 4 5 6])
% (2)randi([a,b],m,n)函数可在指定区间[a,b]内随机取出大小为m*n的整数矩阵
randi([-5,5],2,6)
%% (2)代码求解
min_money = +Inf; % 初始化最小的花费为无穷大,后续只要找到比它小的就更新
min_result = randi([1, 6],1,5); % 初始化五本书都在哪一家书店购买,后续我们不断对其更新
%若min_result = [5 3 6 2 3],则解释为:第1本书在第5家店买,第2本书在第3家店买,第3本书在第6家店买,第4本书在第2家店买,第5本书在第3家店买
n = 100000; % 蒙特卡罗模拟的次数
M = [18 39 29 48 59
24 45 23 54 44
22 45 23 53 53
28 47 17 57 47
24 42 24 47 59
27 48 20 55 53]; % m_ij 第j本书在第i家店的售价
freight = [10 15 15 10 10 15]; % 第i家店的运费
for k = 1:n % 开始循环
result = randi([1, 6],1,5); % 在1-6这些整数中随机抽取一个1*5的向量,表示这五本书分别在哪家书店购买
index = unique(result); % 在哪些商店购买了商品,因为我们等下要计算运费
money = sum(freight(index)); % 计算买书花费的运费
% 计算总花费:刚刚计算出来的运费 + 五本书的售价
for i = 1:5
money = money + M(result(i),i);
end
if money < min_money % 判断刚刚随机生成的这组数据的花费是否小于最小花费,如果小于的话
min_money = money % 我们更新最小的花费
min_result = result % 用这组数据更新最小花费的结果
end
end
min_money % 18+39+48+17+47+20
min_result
%% 蒙特卡罗用于模拟导弹追击问题
% 注意,模拟导弹追击问题更像是一种仿真模拟的方法。这里本质上没有用到随机数,因此严格意义上不能称为蒙特卡罗。
clear;clc
%% (1)预备知识
% mod(m,n)表示求m/n的余数
mod(8,3)
mod(1000,50)
% 设置横纵坐标的范围并标上字符
x = 1:0.01:3;
y = x .^ 2;
plot(x,y) % 画出x和y的图形
axis([0 3 0 10]) % 设置横坐标范围为[0, 3] 纵坐标范围为[0, 10]
pause(3) % 暂停3秒后再继续接下来的命令
text(2,4,'清风') % 在坐标为(2,4)的点上标上字符串:清风
close % 关闭图形窗口
%% (2) 代码求解
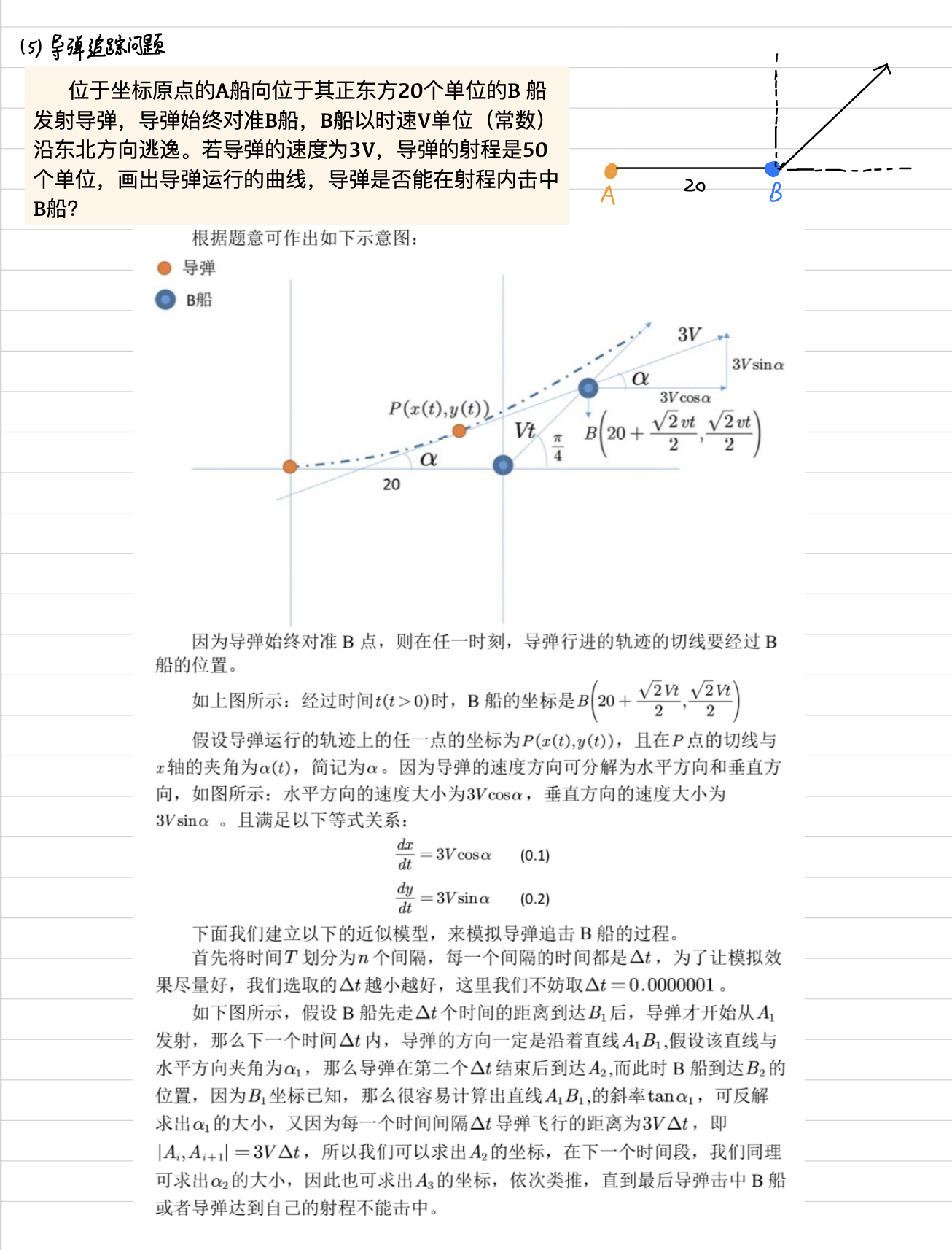
% 1. 不画追击的示意图
clear;clc
v=200; % 任意给定B船的速度(后期我们可以再改的)
dt=0.0000001; % 定义时间间隔
x=[0,20]; % 定义导弹和B船的横坐标分别为x(1)和x(2)
y=[0,0]; % 定义导弹和B船的纵坐标分别为y(1)和y(2)
t=0; % 初始化导弹击落B船的时间
d=0; % 初始化导弹飞行的距离
m=sqrt(2)/2; % 将sqrt(2)/2定义为一个常量,使后面看起来很简洁
dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2); % 导弹与B船的距离
while(dd>=0.001) % 只要两者的距离足够大,就一直循环下去。(两者距离足够小时表示导弹击中,这里的临界值要结合dt来取,否则可能导致错过交界处的情况)
t=t+dt; % 更新导弹击落B船的时间
d=d+3*v*dt; % 更新导弹飞行的距离
x(2)=20+t*v*m; y(2)=t*v*m; % 计算新的B船的位置 (注:m=sqrt(2)/2)
dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2); % 更新导弹与B船的距离
tan_alpha=(y(2)-y(1))/(x(2)-x(1)); % 计算斜率,即tan(α)
cos_alpha=sqrt(1/(1+tan_alpha^2)); % sec(α)^2 = (1+tan(α)^2)
sin_alpha=sqrt(1-cos_alpha^2); % sin(α)^2 +cos(α)^2 = 1
x(1)=x(1)+3*v*dt*cos_alpha; y(1)=y(1)+3*v*dt*sin_alpha; % 计算新的导弹的位置
if d>50 % 导弹的有效射程为50个单位
disp('导弹没有击中B船');
break; % 退出循环
end
if d<=50 & dd<0.001 % 导弹飞行的距离小于50个单位且导弹和B船的距离小于0.001(表示击中)
disp(['导弹飞行',num2str(d),'单位后击中B船'])
disp(['导弹飞行的时间为',num2str(t*60),'分钟'])
end
end
% 2. 画追击的示意图
clear;clc
v=200; % 任意给定B船的速度(后期我们可以再改的)
dt=0.0000001; % 定义时间间隔
x=[0,20]; % 定义导弹和B船的横坐标分别为x(1)和x(2)
y=[0,0]; % 定义导弹和B船的纵坐标分别为y(1)和y(2)
t=0; % 初始化导弹击落B船的时间
d=0; % 初始化导弹飞行的距离
m=sqrt(2)/2; % 将sqrt(2)/2定义为一个常量,使后面看起来很简洁
dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2); % 导弹与B船的距离
for i=1:2
plot(x(i),y(i),'.k','MarkerSize',1); % 画出导弹和B船所在的坐标,点的大小为1,颜色为黑色(k),用小点表示
grid on; % 打开网格线
hold on; % 不关闭图形,继续画图
end
axis([0 30 0 10]) % 固定x轴的范围为0-30 固定y轴的范围为0-10
k = 0; % 引入一个变量 为了控制画图的速度(因为Matlab中画图的速度超级慢)
while(dd>=0.001) % 只要两者的距离足够大,就一直循环下去。(两者距离足够小时表示导弹击中,这里的临界值要结合dt来取,否则可能导致错过交界处的情况)
t=t+dt; % 更新导弹击落B船的时间
d=d+3*v*dt; % 更新导弹飞行的距离
x(2)=20+t*v*m; y(2)=t*v*m; % 计算新的B船的位置 (注:m=sqrt(2)/2)
dd=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2); % 更新导弹与B船的距离
tan_alpha=(y(2)-y(1))/(x(2)-x(1)); % 计算斜率,即tan(α)
cos_alpha=sqrt(1/(1+tan_alpha^2)); % 利用公式:sec(α)^2 = (1+tan(α)^2) 计算出cos(α)
sin_alpha=sqrt(1-cos_alpha^2); % 利用公式: sin(α)^2 +cos(α)^2 = 1 计算出sin(α)
x(1)=x(1)+3*v*dt*cos_alpha; y(1)=y(1)+3*v*dt*sin_alpha; % 计算新的导弹的位置
k = k +1 ;
if mod(k,500) == 0 % 每刷新500次时间就画出下一个导弹和B船所在的坐标 mod(m,n)表示求m/n的余数
for i=1:2
plot(x(i),y(i),'.k','MarkerSize',1);
hold on; % 不关闭图形,继续画图
end
pause(0.001); % 暂停0.001s后再继续下面的操作
end
if d>50 % 导弹的有效射程为50个单位
disp('导弹没有击中B船');
break; % 退出循环
end
if d<=50 & dd<0.001 % 导弹飞行的距离小于50个单位且导弹和B船的距离小于0.001(表示击中)
disp(['导弹飞行',num2str(d),'个单位后击中B船'])
disp(['导弹飞行的时间为',num2str(t*60),'分钟'])
end
end
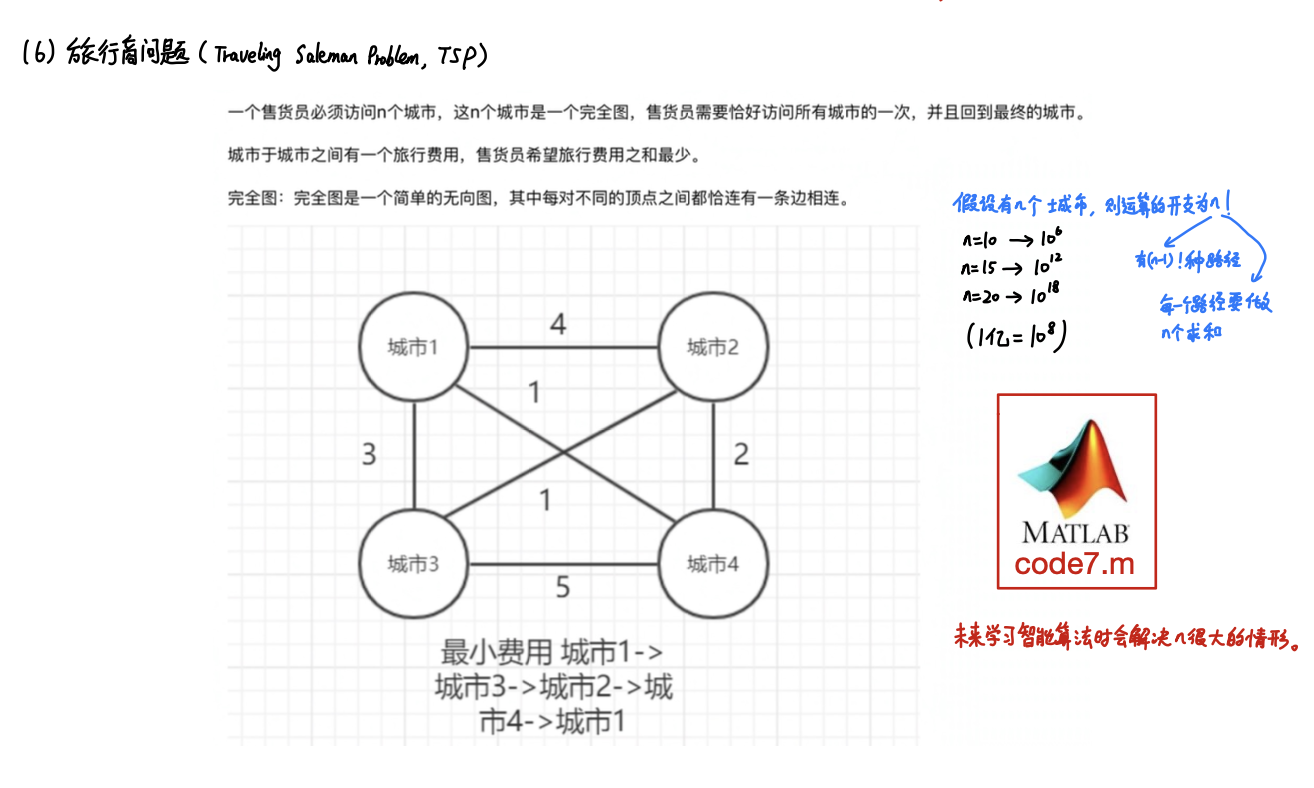
%% TSP(旅行商问题)
%% (1)预备知识
plot([1,2],[5,10],'-o') % 画出一条线段,x范围是[1, 2] ,y范围是[5,10]
text(1.5,7.5,'清风') % 在坐标(1.5,7.5)处标上文本:清风
close
% randperm函数的用法
randperm(5) % 生成1-5组成的一个随机序列(类似于洗牌的操作)
% 3 5 1 2 4
% 1 4 5 3 2
%% (2)代码求解
clear;clc
% 只有10个城市的简单情况
coord =[0.6683 0.6195 0.4 0.2439 0.1707 0.2293 0.5171 0.8732 0.6878 0.8488 ;
0.2536 0.2634 0.4439 0.1463 0.2293 0.761 0.9414 0.6536 0.5219 0.3609]' ; % 城市坐标矩阵,n行2列
% 38个城市,TSP数据集网站(http://www.tsp.gatech.edu/world/djtour.html) 上公测的最优结果6656。
% coord = [11003.611100,42102.500000;11108.611100,42373.888900;11133.333300,42885.833300;11155.833300,42712.500000;11183.333300,42933.333300;11297.500000,42853.333300;11310.277800,42929.444400;11416.666700,42983.333300;11423.888900,43000.277800;11438.333300,42057.222200;11461.111100,43252.777800;11485.555600,43187.222200;11503.055600,42855.277800;11511.388900,42106.388900;11522.222200,42841.944400;11569.444400,43136.666700;11583.333300,43150.000000;11595.000000,43148.055600;11600.000000,43150.000000;11690.555600,42686.666700;11715.833300,41836.111100;11751.111100,42814.444400;11770.277800,42651.944400;11785.277800,42884.444400;11822.777800,42673.611100;11846.944400,42660.555600;11963.055600,43290.555600;11973.055600,43026.111100;12058.333300,42195.555600;12149.444400,42477.500000;12286.944400,43355.555600;12300.000000,42433.333300;12355.833300,43156.388900;12363.333300,43189.166700;12372.777800,42711.388900;12386.666700,43334.722200;12421.666700,42895.555600;12645.000000,42973.333300];
n = size(coord,1); % 城市的数目
figure(1) % 新建一个编号为1的图形窗口
plot(coord(:,1),coord(:,2),'o'); % 画出城市的分布散点图
for i = 1:n
text(coord(i,1)+0.01,coord(i,2)+0.01,num2str(i)) % 在图上标上城市的编号(加上0.01表示把文字的标记往右上方偏移一点)
end
hold on % 等一下要接着在这个图形上画图的
d = zeros(n); % 初始化两个城市的距离矩阵全为0
for i = 2:n
for j = 1:i
coord_i = coord(i,:); x_i = coord_i(1); y_i = coord_i(2); % 城市i的横坐标为x_i,纵坐标为y_i
coord_j = coord(j,:); x_j = coord_j(1); y_j = coord_j(2); % 城市j的横坐标为x_j,纵坐标为y_j
d(i,j) = sqrt((x_i-x_j)^2 + (y_i-y_j)^2); % 计算城市i和j的距离
end
end
d = d+d'; % 生成距离矩阵的对称的一面
min_result = +inf; % 假设最短的距离为min_result,初始化为无穷大,后面只要找到比它小的就对其更新
min_path = [1:n]; % 初始化最短的路径就是1-2-3-...-n
N = 10000000; % 蒙特卡罗模拟的次数
for k = 1:N % 开始循环
result = 0; % 初始化走过的路程为0
path = randperm(n); % 生成一个1-n的随机打乱的序列
for i = 1:n-1
result = d(path(i),path(i+1)) + result; % 按照这个序列不断的更新走过的路程这个值
end
result = d(path(1),path(n)) + result; % 别忘了加上从最后一个城市返回到最开始那个城市的距离
if result < min_result % 判断这次模拟走过的距离是否小于最短的距离,如果小于就更新最短距离和最短的路径
min_path = path;
min_result = result
end
end
min_path
min_path = [min_path,min_path(1)]; % 在最短路径的最后面加上一个元素,即第一个点(我们要生成一个封闭的图形)
n = n+1; % 城市的个数加一个(紧随着上一步)
for i = 1:n-1
j = i+1;
coord_i = coord(min_path(i),:); x_i = coord_i(1); y_i = coord_i(2);
coord_j = coord(min_path(j),:); x_j = coord_j(1); y_j = coord_j(2);
plot([x_i,x_j],[y_i,y_j],'-') % 每两个点就作出一条线段,直到所有的城市都走完
pause(0.5) % 暂停0.5s再画下一条线段
hold on
end