目录
- 二分图算法总览
- 二分图的概念
- 1.二分图的定义
- 2.二分图的特点
- 3.二分图的应用
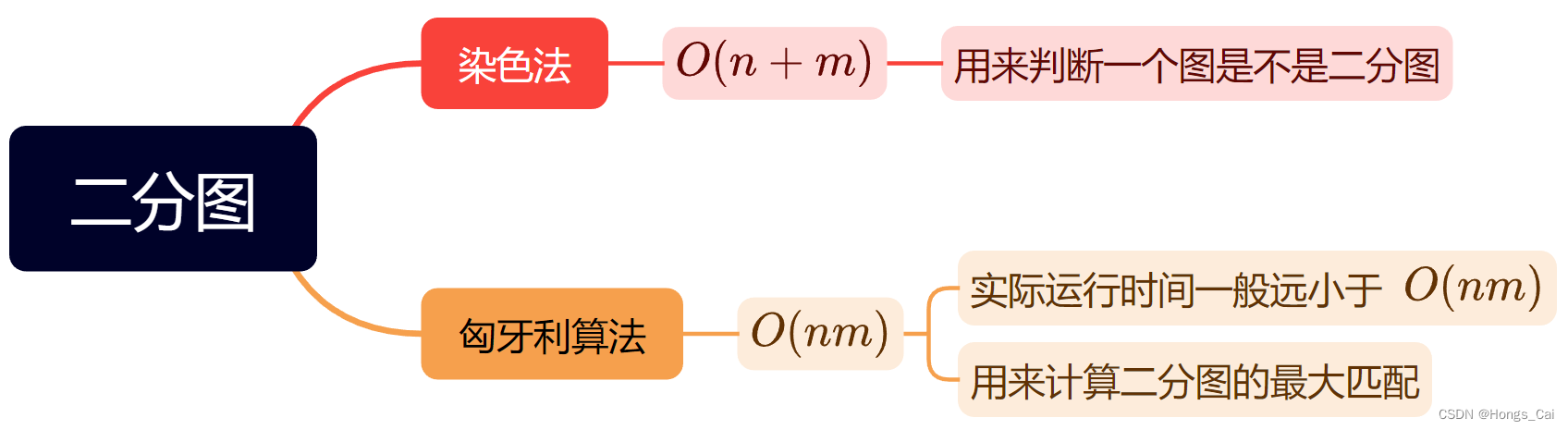
- 染色法(判断二分图)
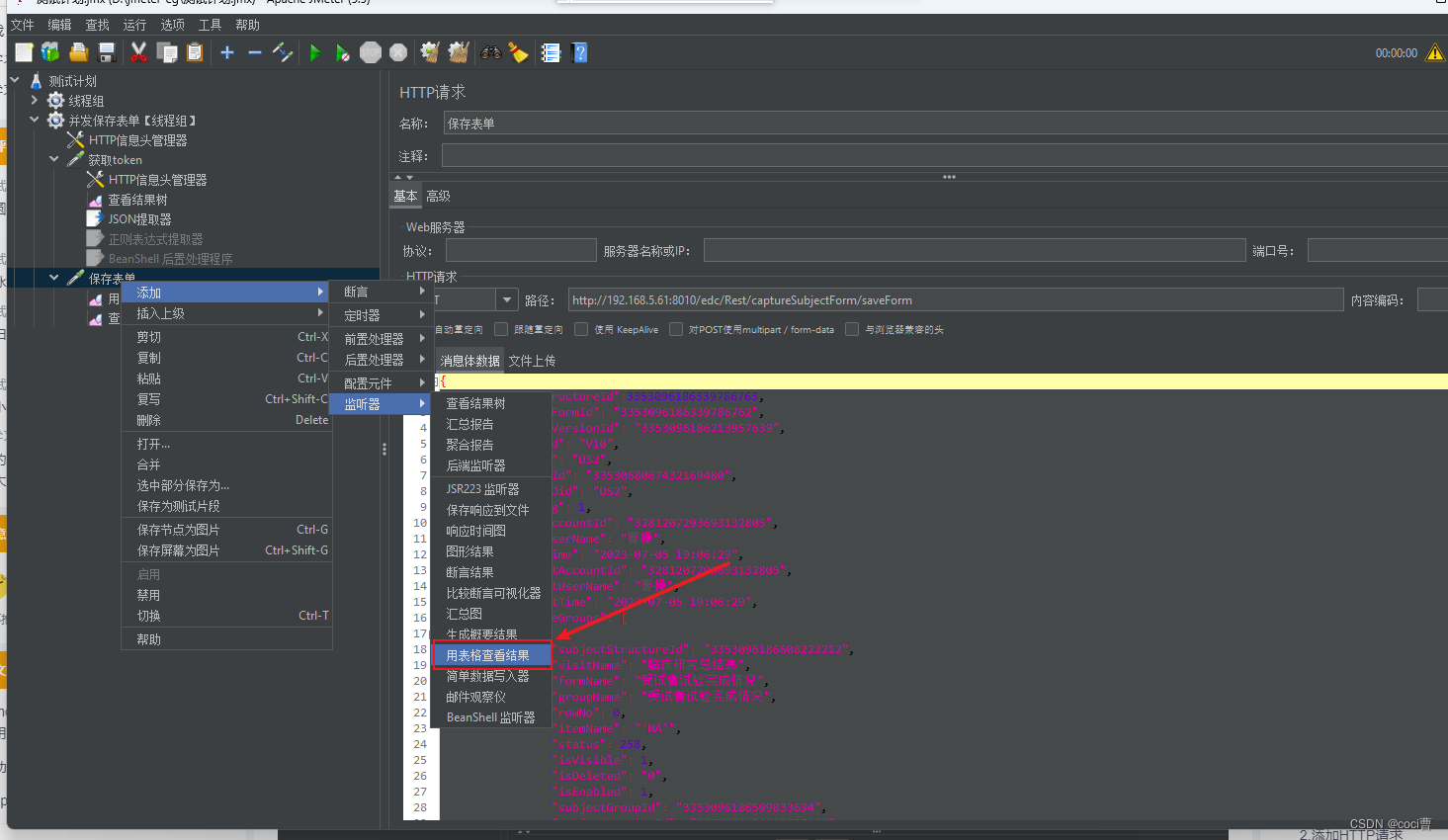
- 算法步骤
- 算法运用
- 染色法判定二分图
- 匈牙利算法(计算二分图的最大匹配)
- 二分图的匹配
- 算法步骤
- 算法应用
- 二分图的最大匹配
二分图算法总览
二分图的概念
1.二分图的定义
一个图 G = ( V , E ) G=(V,E) G=(V,E) 被称为二分图(Bipartite Graph),当且仅当顶点集 V V V 可以分割成两个互不相交的子集 U U U 和 W W W,使得 E E E 中的每一条边都连接一个 U U U 中的顶点和一个 W W W 中的顶点。
换句话说,二分图就是图中的顶点可以分成两类,每条边都只连接这两类顶点中的一个。
例如:
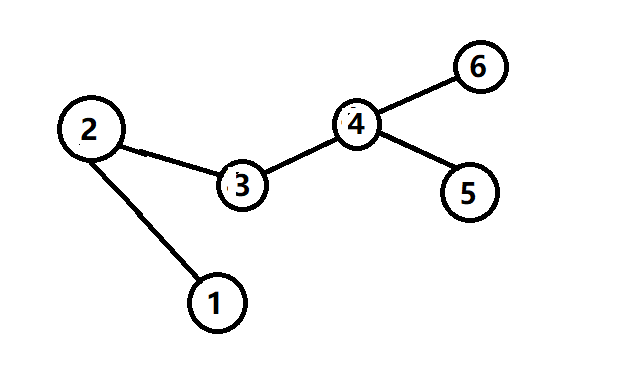
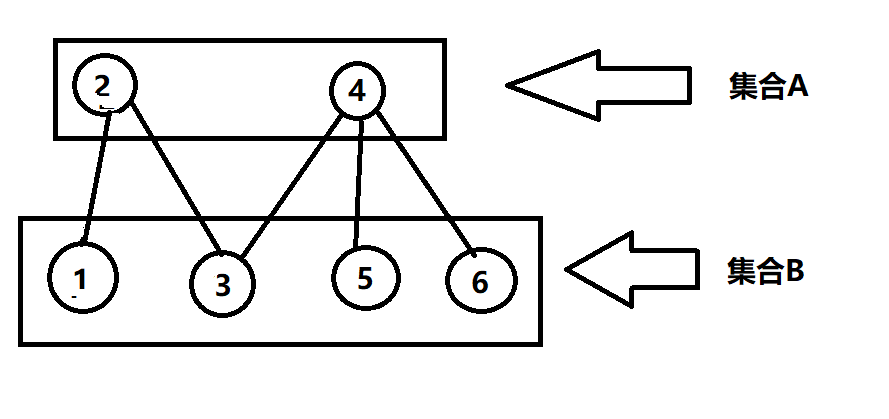
这就是一个明显的二分图,集合A与B中的点互不相连。
2.二分图的特点
- 图 G G G 中的顶点可以分成两个互不相交的子集 U U U 和 W W W, V = U ∪ W V=U∪W V=U∪W。
- 对于任意一条边 ( u , w ) (u,w) (u,w),必有 u ∈ U u∈U u∈U, w ∈ W w∈W w∈W。也就是说,每条边都连接 U U U 和 W W W 中的顶点。
- 不存在属于同一顶点集的两点之间有边相连。 U U U 中的顶点只连接 W W W 中的顶点, W W W 中的顶点只连接 U U U 中的顶点。
- 一个图是二分图,当且仅当它不包含奇数长度的环。
注意:
- 二分图当且仅当图中没有奇数环
- 当图中没有奇数环一定是二分图
- 任何无回路的图均是二分图

- 二分图不一定是连通图
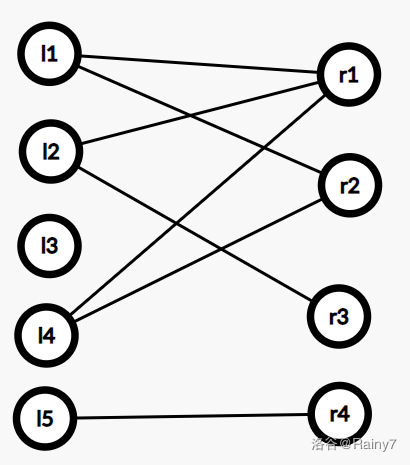
3.二分图的应用
二分图的一些常见应用场景包括:
-
匹配问题
二分图可以用于描述匹配关系。例如,在求解Stable Marriage问题时,男生集合和女生集合构成二分图的两个顶点集,边表示男生和女生之间的偏好。求解这个二分图的最大匹配,就可以得到一个稳定的匹配方案。 -
网络流问题
很多网络流问题可以建模为二分图。例如在网络最大流问题中,源点集和汇点集分别作为二分图的两个顶点集,边和边上的流量构成二分图。求解这个二分图的最大流就等价于求原网络的最大流。 -
图的着色问题
如果将每个颜色看成一个顶点集,图的节点看成另一个顶点集,则图的着色问题可以转换为在对应的二分图中求最大匹配。 -
关系建模
二分图可以建模表达两个不同类型实体集合之间的关系。例如,学生-课程的关系可以用学生集合和课程集合构成的二分图来表示。 -
调度问题
将任务看成一个顶点集,处理器资源看成另一个顶点集,二分图的边表示任务和处理器之间的关系,求解二分图的最大匹配可以用于调度资源。
染色法(判断二分图)
染色法是判断图是否为二分图的一种算法。
基本思想是:
①为图 G G G 中的每个顶点赋予红色或蓝色这两种不同的颜色。
②如果存在一条边的两个端点颜色相同,则该图不是二分图。
③如果所有的边两端点颜色均不同,则该图是二分图。
算法步骤
-
创建一个标记数组 c o l o r [ ] color[ ] color[],将所有顶点标记为未染色,初始化为 0 0 0。
-
遍历所有顶点,对于每个未染色的顶点 v v v:
(1) 使用红色或蓝色对其染色, c o l o r [ v ] = 1 color[v] = 1 color[v]=1 或 2 2 2。
(2) 将与顶点 v v v 相连的所有顶点染成不同颜色。 -
检查每条边的两个端点颜色是否不同:
(1) 若存在一条边其两个端点颜色相同,则返回false,该图不是二分图。
(2) 若所有边两端点颜色均不同,则返回true,该图是二分图。
分析:
- 时间复杂度 O ( n + m ) O(n + m) O(n+m),需要遍历所有顶点和边。
- 空间复杂度 O ( n ) O(n) O(n),需要颜色标记数组。
- 可以在线性时间内判断二分图,效率较高。
算法运用
染色法判定二分图
题目描述:
给定一个
n
n
n 个点
m
m
m 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式:
第一行包含两个整数
n
n
n 和
m
m
m。
接下来 m m m 行,每行包含两个整数 u u u 和 v v v,表示点 u u u 和点 v v v 之间存在一条边。
输出格式:
如果给定图是二分图,则输出 Yes,否则输出 No。
数据范围:
1
≤
n
,
m
≤
1
0
5
1≤n,m≤10^5
1≤n,m≤105
输入样例:
4 4
1 3
1 4
2 3
2 4
输出样例:
Yes
代码实现:
这里采用DFS实现,其实也可以用BFS实现。
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10; // 定义最大顶点数
int h[N], e[N], ne[N], idx; // 邻接表相关数组
int n, m; // n为顶点数,m为边数
int color[N]; // 记录顶点颜色,初始化为0,表示未访问过
// 添加边的函数
void add(int a, int b)
{
e[idx] = b; // 边的终点
ne[idx] = h[a]; // 与顶点a相连的上一条边的编号
h[a] = idx++; // h[a]存储与顶点a相连的最后一条边的编号
}
// 深度优先搜索函数,用于判断图是否为二分图
bool dfs(int u, int c)
{
color[u] = c; // 将顶点u标记为颜色c
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i]; // 与顶点u相连的顶点j
if (!color[j] && !dfs(j, 3 - c)) // 如果顶点j未被标记且与顶点u颜色相反,则递归调用dfs函数
return false; // 如果递归返回false,说明不是二分图,直接返回false
else if (color[j] == c) // 如果顶点j已被标记,并且颜色与顶点u相同,说明不是二分图,返回false
return false;
}
return true; // 如果顶点u及其邻接点都符合二分图定义,则返回true
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
memset(h, -1, sizeof h); // 初始化邻接表数组为-1
cin >> n >> m; // 输入顶点数和边数
for (int i = 0; i < m; ++i)
{
int a, b;
cin >> a >> b; // 输入边的两个顶点
add(a, b), add(b, a); // 添加无向边
}
bool flag = true; // 初始化标志位为true
for (int i = 1; i <= n; ++i)
{
if (!color[i] && !dfs(i, 1)) // 对每个未被标记的顶点进行dfs,如果返回false,则不是二分图
{
flag = false; // 将标志位设为false
break; // 直接跳出循环
}
}
if (flag) // 如果标志位为true,输出"Yes"
cout << "Yes" << endl;
else // 否则输出"No"
cout << "No" << endl;
return 0;
}
tip:
妙用
3
−
c
3 - c
3−c 来表示与当前顶点相反的颜色。
扩展问题:
关押罪犯
匈牙利算法(计算二分图的最大匹配)
匈牙利算法(Hungarian algorithm)是用于解决二分图最大匹配问题。其基本思想是通过寻找增广路径来不断增加匹配的边数,直到无法找到新的增广路径为止。
二分图的匹配
-
二分图的匹配:给定一个二分图 G G G,在 G G G 的一个子图 M M M 中, M M M 的边集 E E E 中的任意两条边都不依附于同一个顶点,则称 M M M 是一个匹配。
-
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
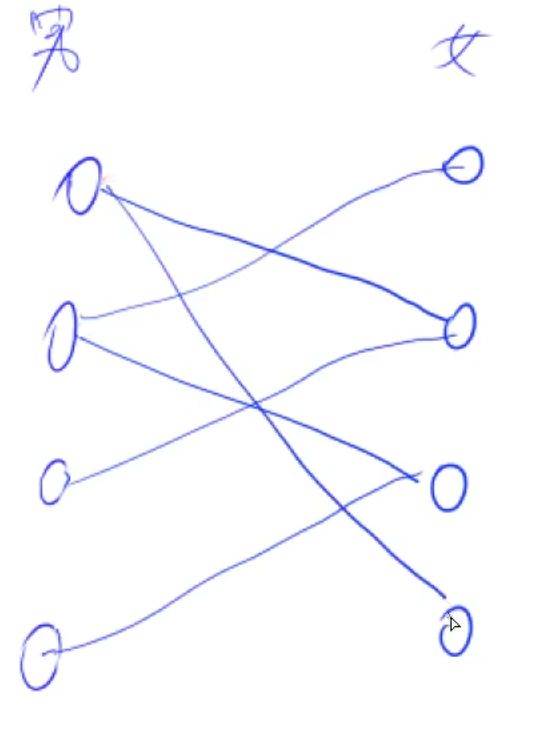
匹配前:
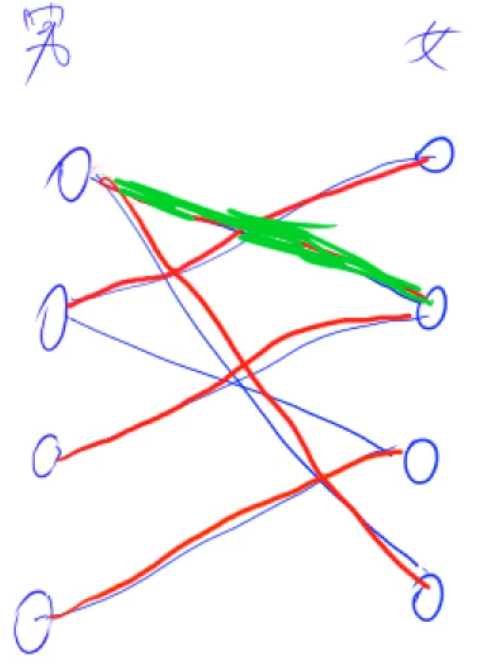
匹配后:
算法步骤
下面是匈牙利算法的具体步骤:
-
初始化:将所有顶点的匹配状态置为未匹配( m a t c h match match 数组初始化为 0 0 0)。
-
遍历左侧顶点:对于二分图的每个左侧顶点i,开始寻找增广路径。
- 将当前左侧顶点i的状态数组 s t st st 初始化为 f a l s e false false,用于标记增广路径中的顶点是否已经被访问。
- 对当前左侧顶点 i i i,尝试在其邻接表中寻找一个未匹配的右侧顶点 j j j(如果存在),或者找到一个能够与右侧顶点 j j j 存在增广路径的未匹配顶点。
- 若找到这样的顶点 j j j,则将右侧顶点 j j j 与左侧顶点i进行匹配(即将 m a t c h [ j ] match[j] match[j] 设置为 i i i),表示找到一条增广路径。
-
增加匹配数:在找到一条增广路径后,将匹配数 r e s res res 加 1 1 1。
-
重复步骤 2 2 2 和步骤 3 3 3:重复执行上述步骤,直到无法找到新的增广路径为止。
-
输出结果:最终匹配的边数 r e s res res 即为二分图的最大匹配数。
算法应用
二分图的最大匹配
题目描述:
给定一个二分图,其中左半部包含
n
1
n_1
n1 个点(编号
1
∼
n
1
1∼n_1
1∼n1),右半部包含
n
2
n_2
n2 个点(编号
1
∼
n
2
1∼n_2
1∼n2),二分图共包含
m
m
m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
输入格式:
第一行包含三个整数
n
1
、
n
2
和
m
n_1、 n_2 和 m
n1、n2和m。
接下来 m m m 行,每行包含两个整数 u u u 和 v v v,表示左半部点集中的点 u u u 和右半部点集中的点 v v v 之间存在一条边。
输出格式:
输出一个整数,表示二分图的最大匹配数。
数据范围:
1
≤
n
1
,
n
2
≤
500
1≤n_1,n_2≤500
1≤n1,n2≤500
1
≤
u
≤
n
1
1≤u≤n_1
1≤u≤n1
1
≤
v
≤
n
2
1≤v≤n_2
1≤v≤n2
1
≤
m
≤
1
0
5
1≤m≤10^5
1≤m≤105
输入样例:
2 2 4
1 1
1 2
2 1
2 2
输出样例:
2
代码实现:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510, M = 1e5 + 10;
int n1, n2, m;
bool st[N]; // 数组用于在DFS过程中标记访问过的节点
int h[N], e[M], ne[M], idx, match[N]; // 图的表示和匹配数组
void add(int a, int b)
{
e[idx] = b; // 将节点 'b' 添加到节点 'a' 的邻接表中
ne[idx] = h[a]; // 更新节点 'a' 的邻接表指针
h[a] = idx++; // 更新节点 'a' 的邻接表头指针,idx自增表示下一个插入的边的索引
}
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i]; // j为节点x的邻居节点
if (st[j]) continue; // 如果节点j已经被访问过,则跳过
st[j] = true; // 标记节点j为已访问
if (match[j] == 0 || find(match[j])) // 如果节点j未匹配或者节点j的匹配节点能够寻找到增广路径
{
match[j] = x; // 将节点x匹配给节点j
return true; // 返回成功匹配
}
}
return false; // 无法找到增广路径,返回失败
}
int main()
{
cin.tie(0); // 提高输入输出的效率
ios::sync_with_stdio(false); // 关闭输入输出流的同步
int res = 0; // 最大匹配数初始化为0
memset(h, -1, sizeof h); // 初始化邻接表头指针为-1
cin >> n1 >> n2 >> m; // 输入图的节点数和边数
for (int i = 0; i < m; ++i)
{
int a, b;
cin >> a >> b; // 输入图的边
add(a, b); // 将边添加到邻接表中
}
for (int i = 1; i <= n1; ++i)
{
memset(st, false, sizeof st); // 每次匹配前都要将访问数组st重置为false
if (find(i)) res++; // 尝试将节点i匹配,如果匹配成功,则最大匹配数加1
}
cout << res << endl; // 输出最大匹配数
}
扩展问题:
棋盘覆盖