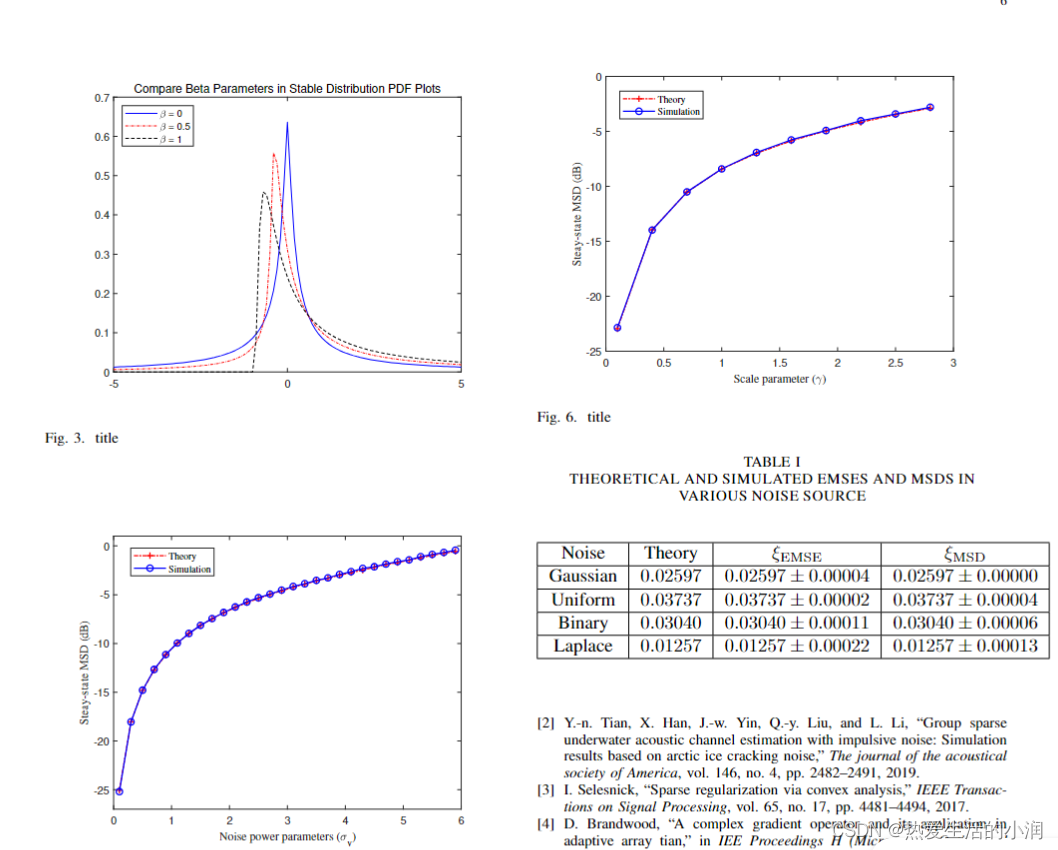
文章目录
- [ 打牌](https://ac.nowcoder.com/acm/contest/60063/F)
- 问题建模
- 问题分析
- 代码
打牌


问题建模
给出三个长度为3的字符串,每个字符串仅由’w’,‘i’,‘n’三种字符组成,以及回合数n,每一个回合每一个字符串选择一个字符向其下一个字符串传递,问在n个回合内第一个字符串同时含有’w’,‘i’,'n’的概率为多少。
问题分析
对于输入的字符串,可以看做是一个初始局面,后面每一个回合中的字符选择都是一次变化,可以将输入的字符存入一个二维矩阵来表示当前局面的状态,每一个回合遍历所有字符传递的情况来表示,局面状态的转移。
代码
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
const int N =30,INF=0x3f3f3f3f,Mod=1e9+7;
string strt="win";
int k[5][5];
int n;
int to(char c){
for(int i=0;i<2;i++){
if(c==strt[i]) return i;
}
return 2;
}
LL qmi(LL x,LL y,LL p){
LL res=1;
x%=p;
while(y){
if(y&1) res=(res*x)%p;
x=(x*x)%p;
y>>=1;
}
return res;
}
LL dfs(int u){
LL res=0;
for(int i=1;i<=3;i++){
///当有人获胜时,当前回合结束
if(k[i][0]==k[i][1]&&k[i][1]==k[i][2]) return i==1;
}
if(u==n) return 0;
for(int i=0;i<3;i++){
///仅考虑能让阿宁获胜转移情况,即该字符有多才转移
if(k[1][i]<=1) continue;
for(int j=0;j<3;j++){
if(k[2][j]==0) continue;
for(int z=0;z<3;z++){
if(k[3][z] == 0)continue;
///确定阿宁给出字符后,将另外两个的情况相乘获得该局面的状态数
LL p2=(LL)k[2][j]*k[3][z]*qmi(9,Mod-2,Mod)%Mod;
///状态转移
k[1][i]--,k[1][z]++;
k[2][j]--,k[2][i]++;
k[3][z]--,k[3][j]++;
res=(res+dfs(u+1)*p2%Mod)%Mod;
k[1][i]++,k[1][z]--;
k[2][j]++,k[2][i]--;
k[3][z]++,k[3][j]--;
}
}
}
return res;
}
void solve() {
cin >>n;
for(int i=1;i<=3;i++){
string str;
cin >>str;
for(int j=0;j<3;j++){
将输入的字符串,转换为状态矩阵
k[i][to(str[j])]++;
}
}
cout <<dfs(0) <<"\n";
}
int main() {
int t = 1;
//cin >> t;
while (t--) solve();
return 0;
}