题目

313. 超级丑数【中等】

题解

之前做过丑数，规定丑数是质因数只包含2,3,5的正整数，而这道题丑数升级为超级丑数，规定为包含的质因数是在primes数组中的正整数

丑数的题解用动态规划，那么超级丑数也可以利用相同的方法解答

状态定义：dp[i][j] 表示nums在区间 [0,i−1] 被切分成 j 个子数组的最大平均值和。
状态转移方程：
j=1时，对应[0,i-1]区间的最大平均值
j>1时，将区间分为[0,x-1]，[x,i-1]两个部分，需要列不同的x，看什么时候最大平均值和最大
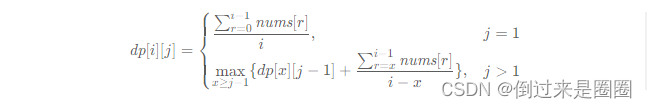
初始条件：
dp[i][1]=prefix[i]/i，其中prefix[i]为前i个数字的前缀和
返回值：dp[n][k]

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        int n=lists.length;
        if(n==0)
            return null;
        ListNode res=lists[0];
        for(int i=1;i<n;i++)
            res=merge2Lists(res,lists[i]);
        return res;
    }
    //合并两个有序链表
    public ListNode merge2Lists(ListNode res,ListNode node){
        ListNode head=new ListNode();
        ListNode p=res,q=node,tail=head;
        while(p!=null&&q!=null){
            if(p.val<q.val){
                tail.next=p;
                p=p.next;
            }
            else{
                tail.next=q;
                q=q.next;
            }
            tail=tail.next;
        }
        while(p!=null){
            tail.next=p;
            p=p.next;
            tail=tail.next;
        }
        while(q!=null){
            tail.next=q;
            q=q.next;
            tail=tail.next;
        }
        return head.next;
    }
}

时间复杂度： $O(k^2n)$ ，假设每个链表的最长长度是n，那么第 i 次合并之后链表最长为i*n，第 i 次合并的时间复杂度是O( $i * n$ )，所以总时间复杂度为 $KaTeX parse error: Undefined control sequence: \* at position 9: O(((1+k)\̲*̲k/2)\*n)$ ，即为 $O(k^2n)$