问题引入
如何检测一个链表是否有环,如果有,那么如何确定环的长度及起点。
引自博客:上述问题是一个经典问题,经常会在面试中被问到。我之前在杭州一家网络公司的电话面试中就很不巧的问到,当时是第一次遇到那个问题(毕竟太菜,没有专门准备过算法面试),我思考片刻,问答的是用一个哈希表存储访问的节点的地址,当访问某节点时,发现哈希表中已存在,表明链表中存在环。面试官听了我的回答就反问了我一句:如果链表的环很大,那么哈希表的空间消耗就很大,你的方法并不实用。你能在不消耗额外空间的情况下,找到链表的环吗?当时,想了很久没想到,面试官就说可以这样做,balabala...
算法描述
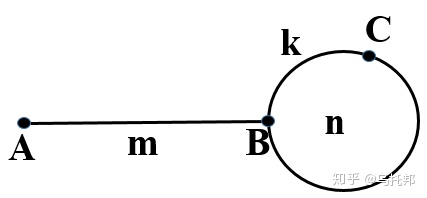
解决上述问题的方法就是我们常说的快慢指针。乌龟与兔子在一个含环的跑道上(如图所求)进行比赛,乌龟在单位时间内移动一步,而兔子则在单位时间内移动两步,其移动速度是乌龟的两倍。乌龟与兔子同时从A点出发,兔子移动的快先行进入环形跑道,但那以后,一直在转圈。所以如果存在环的话,乌龟总能与兔子相遇(首次相遇在C点)。
假设乌龟刚进入环时,兔子在环中任何一位置,此时二者相差距离为m,以后每运动一次兔子两步乌龟一步二者距离减少1,运动几次后距离总能变成0,所以慢指针走一步快指针走两步二者一定能相遇,但慢指针走一步快指针走三步或者其他组合方式可能并不一定能相遇需要注意。
- 判断是否有环
定义两个指针p1与p2,起始时,都指向链表的起点A,p1每次移动1个长度,p2每次移动2个长度。如果p2在移到链表的尾端时,并未与p1相遇,表明链表中不存在环。如果p1与p2相遇在环上的某一点C,表明链表有环。
- 环的长度
将指针p1固定在相遇位置C,移动p2,每次移动1个长度,并用变量cnt计数。当p2再次与p1相遇时,此时cnt的值就是环的长度。
- 环的起点
环的起点即图中点B,将指针p1指向链表的起始位置A,指针p2仍在位置C,指针p1与p2每次均移动一个单位,p1与p2再次相遇的位置就是环的起点位置点B。
简单证明
上面求链表是否存在环及求环的长度的思路都很好理解,主要是为什么p1与p2再次相遇就是环的起点呢?这里假设从跑道的起始点A到环的起点B的路程为m,从B到相遇点C的路程为k,环的长度为n,相遇时乌龟的爬行路程为S1=m+k+t1*n,兔子的奔跑距离为S2=m+k+t2*n(t2>t1),兔子的速度是乌龟的两倍即S2=2*S1,则S1=S2-S1=(t2-t1)*n,S2=2*(t2-t1)*n,即兔子和乌龟相遇时的奔跑距离都为环的整数倍,而m+k=(t2-2*t1)*n也为环的整数倍。当兔子回到跑道的起始位置,乌龟从相遇点B出发时,这时,两人的速度均为单位时间内爬行1个长度,当兔子到达环的起点B即爬行了m距离时,乌龟则是k+m,此时刚好爬行环的整数倍,也处于环的起点B,即乌龟与兔子再次相遇的位置即为环的起点位置B。
参考链接:弗洛伊德的兔子与乌龟