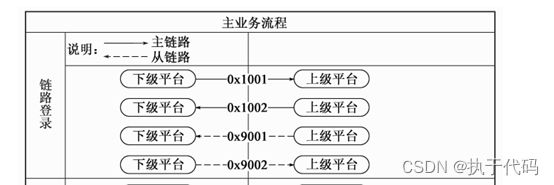
1.VAE的直观理解

先简单了解一下自编码器，也就是常说的Auto-Encoder。Auto-Encoder包括一个编码器（Encoder）和一个解码器（Decoder）。其结构如下：

自编码器是一种先把输入数据压缩为某种编码, 后仅通过该编码重构出原始输入的结构. 从描述来看, AE是一种无监督方法.

AE的结构非常明确, 需要有一个压缩编码的Encoder和就一个相应解码重构的Decoder

那么VAE的目标是什么？为什么VAE呢？

-------VAE作为一个生成模型，其基本思路是很容易理解的：把一堆真实样本通过编码器网络变换成一个理想的数据分布，然后这个数据分布再传递给一个解码器网络，得到一堆生成样本，生成样本与真实样本足够接近的话，就训练出了一个自编码器模型。

为什么要用VAE，原来的Auto Encoder有什么问题呢？那面下面是一个直观的解释。

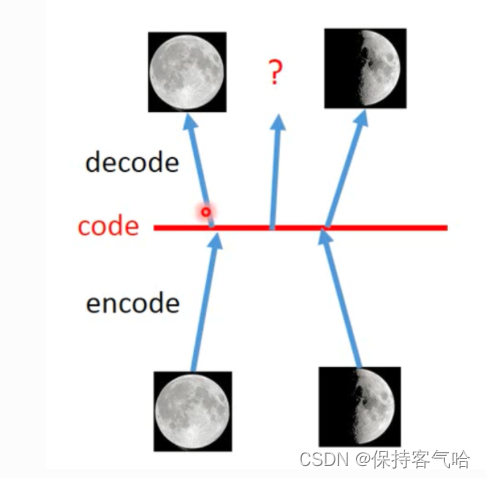
下图是 AutoEncoder 的简单例子：我们把一张满月的图片 Encoder 后得到 code，这个code被decoder 后又转换为满月图，弦月图也是如此。注意它们直接的一对一关系。图片左边那个问号的意思是当对 AE 中的code进行随机采样时，它介于满月与弦月之间的数据，decoder后可能会输出什么？
-------------可能会输出满月，可能会输出弦月，但是最有可能输出的是奇奇怪怪的图片。

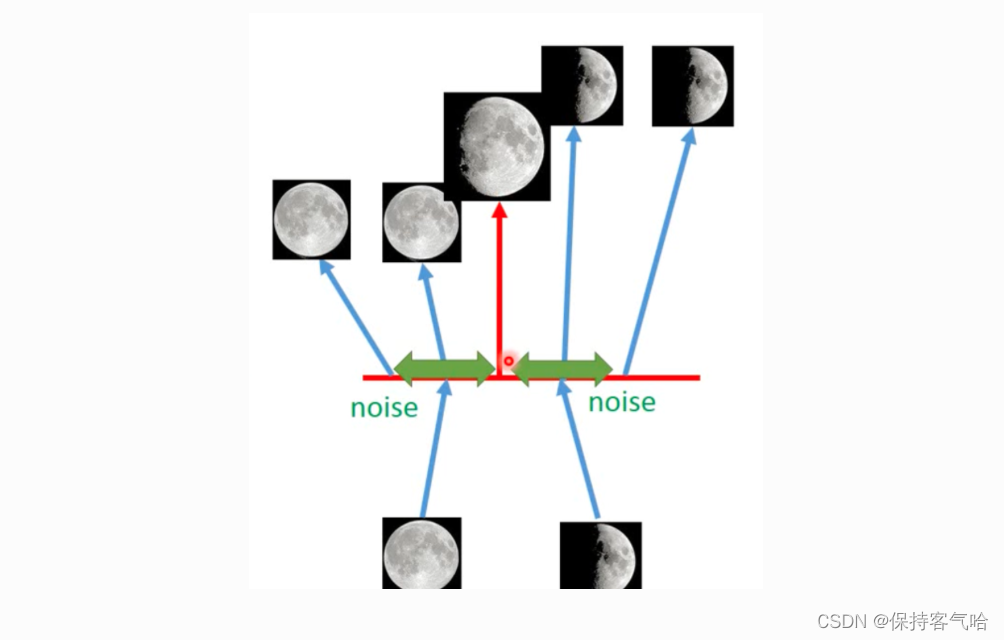
下图是 VAE 的简单例子，我们在 code 中添加一些 noise，这样可以让在满月对应 noise 范围内的code 都可以转换为满月，弦月对应的noise 范围内的code也能转换成弦月。但当我们在不是满月和弦月对应的noise的code中采样时，decoder出来的图片可能是介于满月和弦月之间的图。也就是说，VAE 产生了输入数据中不包含的数据，（可以认为产生了含有某种特定信息的新的数据），而 AE 只能产生尽可能接近或者就是以前的数据（当数据简单时，编码解码损耗少时）。

2.VAE的模型直观展示

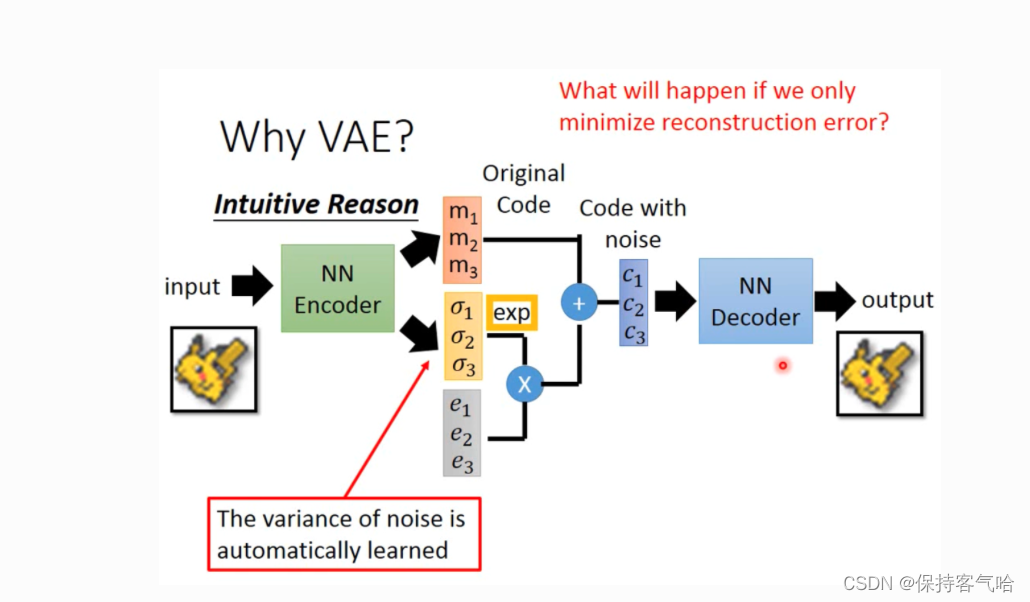
在VAE中，为了给编码添加合适的噪音，编码器会输出两个编码，一个是原有编码$m_1,m_2,m_3$，另外一个是控制噪音干扰程度的编码${\sigma }_1,{\sigma }_2,{\sigma }_3$，第二个编码其实很好理解，就是为随机噪音码$e_1,e_2,e_3$分配权重，然后加上exp的目的是为了保证这个分配的权重是个正值，最后将原编码与噪音编码相加，就得到了VAE在code层的输出结果$c_1,c_2,c_3$。

损失函数方面，除了必要的重构损失外，VAE还增添了一个损失函数，这同样是必要的部分，因为如果不加的话，整个模型就会出现问题：为了保证生成图片的质量越高，编码器肯定希望噪音对自身生成图片的干扰越小，于是分配给噪音的权重越小，这样只需要将${\sigma }_1,{\sigma }_2,{\sigma }_3$赋为接近负无穷大的值就好了。所以，第二个损失函数就有限制编码器走这样极端路径的作用，这也从直观上就能看出来，$exp({\sigma }_i)-(1+{\sigma }_i)$在x=0处取得最小值，于是${\sigma }_1,{\sigma }_2,{\sigma }_3$就会避免被赋值为负无穷大。

3.VAE的基本原理

那先回到我们到底想做什么？我们现在是想要生成图片，就拿下图距离，每张图片可以看做高维空间的一个点，然后这些图片符合一个分布P(x),我们要做的事情就是去预测这个高维空间的概率分布P(x),只要我们知道这个分布我们就可以从中sample然后得到图片。

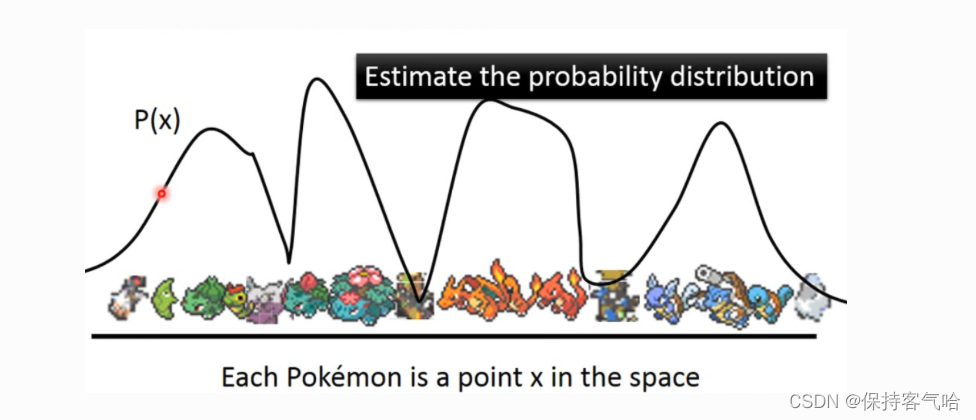
那如何去知道这个分布呢？我们先了解一下什么是高斯混合模型？------------即任何一个数据的分布，都可以看作是若干高斯分布的叠加。

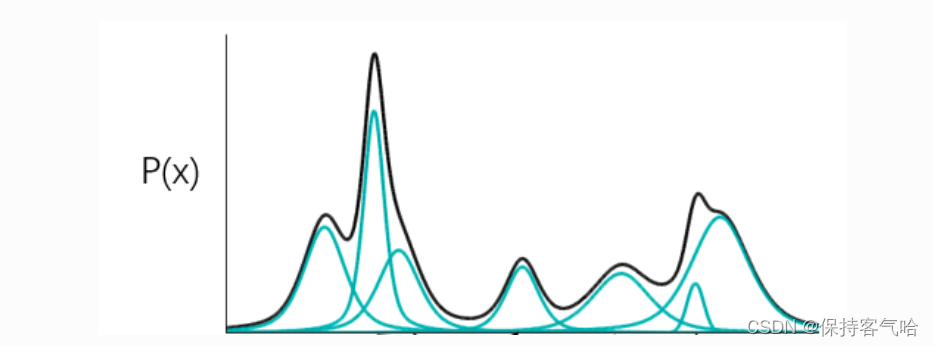
上图中黑色代表的是P(x)分布，蓝色的线都是不同的高斯分布，我们可以用若干个高斯分布去拟合P(x),那如果我们想要从P(x)去sample一个东西，那我们就要去考虑我们是从哪个高斯分布中去sample。然后这个这个过程可以表示为下图

其中最下面的代表的是高斯分布，m代表的是第几个高斯分布，蓝色的柱状图即P(m)代表的是去选择某一个高斯分布(m)的概率，所以P(x)可以表示为黄色标记所示，每个m对应的高斯分布有自己的均值和方差。

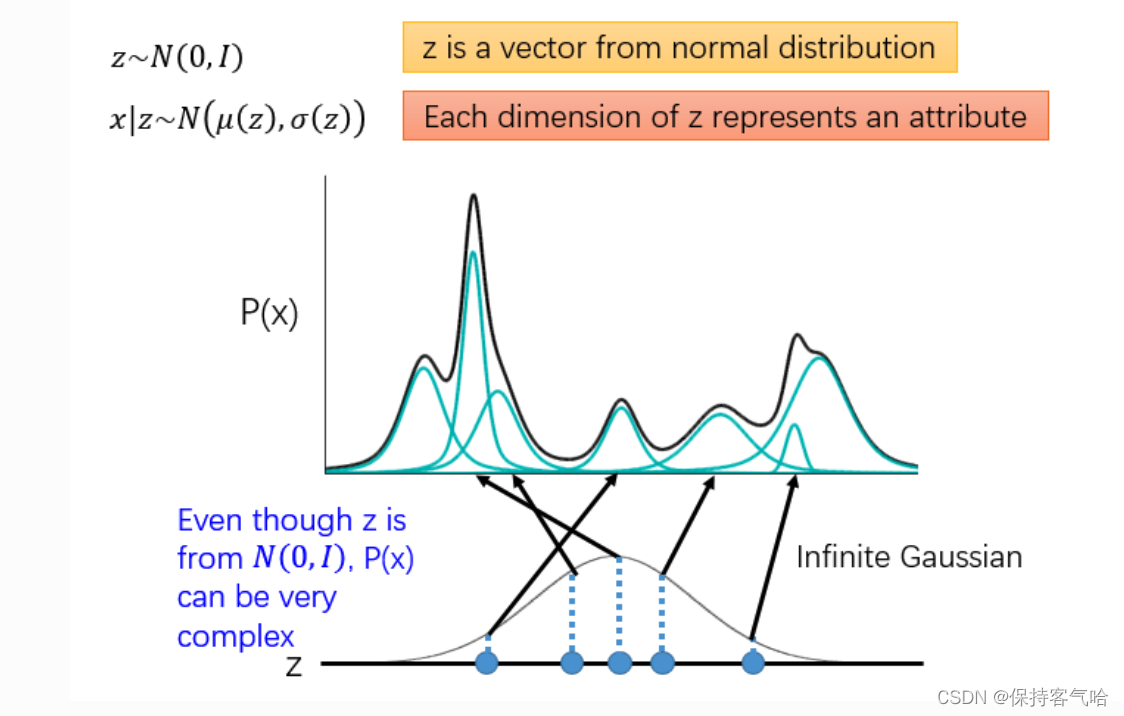
现在我们借助一个变量$ z\sim N(0,I)$ ,(注意z是一个向量，生成自一个高斯分布)，找一个映射关系，将向量z映射成这一系列高斯分布的参数向量$\mu (z)$和$ \sigma (z)$。有了这一系列高斯分布的参数我们就可以得到叠加后的P(x)的形式。也就是说我们只要知道每个高斯分布的参数，我们就能用它拟合P(x)

那么现在$$P(x)=\int P(z)P(x\mid z)dz(1)$$ , 其中$z\sim N(0,I),x|z\sim N(\mu (z),\sigma (z))$

接下来就可以求解这个式子。由于P(z)是已知的，P(x|z)未知，而$x|z\sim N(\mu (z),\sigma (z))$，于是我们真正需要求解的，是$\mu (z)$和$ \sigma (z)$两个函数的表达式。很难直接计算积分部分，因为我们很难穷举出所有的向量z用于计算积分，我们需要引入两个神经网络来帮助我们求解。

• 第一个神经网络在VAE叫做Decoder，它求解的$\mu (z)$和$ \sigma (z)$和两个函数，这等价于求解P(x|z)。

  

• 第二个神经网络在VAE叫做Encoder，它求解的结果是$q(z\mid x)，z|x\sim N({\mu }^{\prime }(x),{\sigma }^{\prime }(x))$，q可以代表任何分布。它主要是用来得到给定一个 x 然后得到对应 z 的${\mu }^{\prime }(x),{\sigma }^{\prime }(x)$

这儿引入第二个神经网络Encoder的目的是，辅助第一个Decoder求解P(x|z)

现在梳理一下我们的目的，我们需要求P(x)，然后P(x)可以表示为：

​ $$P(x)=\int P(z)P(x\mid z)dz$$

我们希望P(x)越大越好，等价于求

​ $$MaxmizeL=\sum _{x}logP(x)$$

又因为

​ $$\log P(x)={\int }_{z}q(z|x)\log P(x)dz$$

因为 $${\int }_{z}q(z|x)dz=1$$

所以

$$\begin{array}{rl}\log P(x)& ={\int }_{z}q(z|x)\log \frac{P(z,x)}{P(z|x)}dz\\ & ={\int }_{z}q(z|x)\log \frac{P(z,x)q(z|x)}{q(z|x)P(z|x)}dz\\ & ={\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz+{\int }_{z}q(z|x)\log \frac{q(z|x)}{P(z|x)}dz\\ & =D_{KL}(q(z|x)||P(z|x))+{\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz\\ & \ge {\int }_{z}q(z|x)\log \frac{P(x|z)P(z)}{q(z|x)}dz\text{since }{D}_{KL}(q||P)\ge 0\end{array}$$

我们将$${\int }_{z}q(z|x)\log \frac{P(x|z)P(z)}{q(z|x)}dz$$ 称为 $\log P(x)$ 的 (variational) lower bound (变分下界)，简称为 $L_b$。

即 原式化简为 $$logP(x)=L_b+KL(q(z|x)||p(z|x))$$

原本，我们需要求$P(x|z)$ 使得$logP(x)$ 最大，现在引入了一个$q(z|x)$，变成了同时求$P(x|z)$和$q(z|x)$使得$logP(x)$最大。实际上，因为后验分布 $P(z|x)$ 很难求 (intractable)，所以才用 $q(z|x)$ 来逼近这个后验分布。在优化的过程中我们发现，首先 $q(z|x)$ 跟 $\log P(x)$ 是完全没有关系的，$\log P(x)$ 只跟 $P(z|x)$ 有关，调节 $q(z|x)$ 是不会影响似然也就是 $\log P(x)$ 的。所以，当我们固定住 $P(x|z)$ 时，调节 $q(z|x)$ 最大化下界 $L_b$，KL 则越小。当 $q(z|x)$ 逼近后验分布 $P(z|x)$ 时，KL 散度趋于为 0，$\log P(x)$ 就和 $L_b$ 等价。所以最大化 $\log P(x)$ 就等价于最大化 $L_b$。

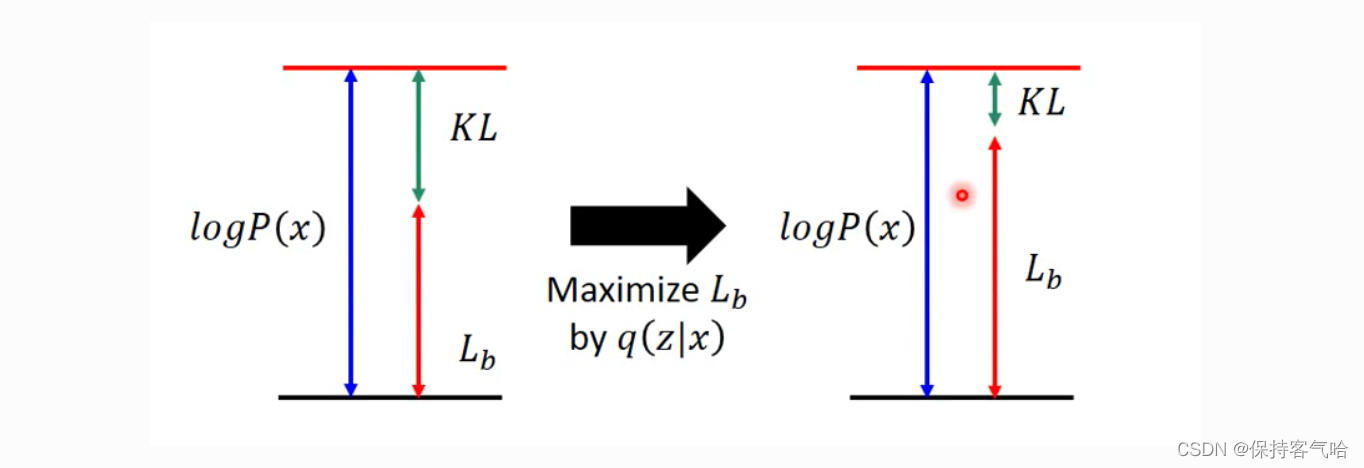
现在我们来求 Maxmize $L_b$

$$\begin{array}{rl}{L}_b& ={\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz\\ & ={\int }_{z}q(z|x)\log \frac{P(x|z)P(z)}{q(z|x)}dz\\ & ={\int }_{z}q(z|x)\log \frac{P(z)}{q(z|x)}dz+{\int }_{z}q(z|x)\log P(x|z)dz\\ & =-D_{KL}(q(z|x)||P(z))+E_{q(z|x)}[\log P(x|z)]\end{array}$$

所以，求解 Maxmize $L_b$，等价于求解KL(q(z|x)||P(z))的最小值和==$ E_{q(z|x)}[\log P(x|z)]$的最大值。==

• 我们先来求第一项，其实 $-D_{KL}(q(z|x)||P(z))$的展开式刚好等于：${\sum }_{i=1}^J(exp({\sigma }_i)-(1-{\sigma }_i)+(m_i{)}^2)$，于是，第一项式子就是第二节VAE模型架构中第二个损失函数的由来,其实就是去调节NN’使得到的q(z|x)与标准正态分布约接近越好

  • 

• 接下来求第二项，注意到Maxmize$ E_{q(z|x)}[\log P(x|z)]$，也就是表明在给定求q(z|x)（编码器输出）的情况下p(x|z)（解码器输出）的值尽可能高，这其实就是一个类似于Auto-Encoder的损失函数（方差忽略不计的话)，过程如下图所示：

  • 

  • 我们要想从q(z|x)中sample一个data，就将x输入到NN中，产生${\mu }^{\prime }(x),{\sigma }^{\prime }(x)$，然后产生z，接下来我们要maxmize z产生x的几率，即要想输出maxmize log P(x|z）就需要让NN的输出$\mu (x)$ 与 x越接近越好