前言

（12月5日）突然想起了很久以前别人（具体来源已经记不清了）传给我的一套题单。网上的题单不少，光收藏可不行，关键还得下手。

这套题单的题目数量为300出头，什么时候刷完我还没有明确计划，但我必定会持续更新（刷题）！小伙伴们如果一起，也可以交流。本文是题单的第一部分——数组，有30道题。

刚开始刷的时候，我的策略是“速度为上”，尽量快点通过避免过多优化代码的质量 （可读性、效率等），打算后面会对代码进行重构。为了快点刷，这次代码基本没写注释（但这可能不是个好习惯）。

先从简单的题目开始刷，积累信心，养成刷题的习惯，然后再慢慢地向难题突破。

小结

12月8日刷完了第一部分——数组，算是成功踏出了第一步。这三十道题大多是力扣中的“简单”和“中等”难度，想不出来时还可以看力扣的题解（独立思考很重要，同时也要兼顾效率，做好平衡），刷题体验较好。第一部分的成功完成也确实给我自己积累了一些信心，觉得自己可以继续走下去了。

令我印象比较深刻的一点是，力扣老喜欢 “原地算法”，即要求仅使用常量级的额外空间完成对数组的操作，这样的要求会给题目带来一些额外的难度。常用的一个方法是对输入或输出数组进行改造，给我们提供操作空间。

题单简介

是不是有许多小伙伴在刷力扣的时候感觉无从下手？从头按顺序开始刷的童鞋们可能会比较有感触，为什么才第四题就感觉很难了?没关系，本文将对力扣的 1-700 题中不需要会员的数据结构与算法题目(数据库与 shell 除外)进行分类，并推荐一个刷题的顺序。

完全零基础可以刷题吗？
不能，至少要基本掌握一门计算机语言的语法。但现在在网上随便搜一下就能搜到许多关于计算机语言的教程。当然，最好还是上一下正规的课程。

刷题顺序很重要吗？
重要。按照题目类别结构化地刷题的速度不仅更快，而且可以在刷完一类题之后进行总结。对于水平较高的小伙伴们来说，按照推荐的顺序刷，可以在 200 小时内刷完 500 多题。对于萌新们来说，按照推荐顺序刷，能更好地掌握数据结构与算法基础。

---

---

数组的遍历 485、495、414、628

485. 最大连续 1 的个数 | 很久以前

//首次通过
class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        int count = 0;
        int countMax = 0;
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] == 1) {
                count ++;
            }
            else {
                count = 0;
            }
            if(count > countMax){
                countMax = count;
            }
        }
        return countMax;
    }
};

495. 提莫攻击 | 很久以前

//首次通过
#include<cstdio>
class Solution {
public:
    int findPoisonedDuration(vector<int>& timeSeries, int duration) {
        int tLast = timeSeries[timeSeries.size() - 1] + duration;
        int len = timeSeries.size();

        int count = 0;
        int iTS = 0;
        for(int i = 0; i < len - 1; i++){
            int mid = timeSeries[i+1] - timeSeries[i];
            int addT = duration < mid ? duration : mid;
            count += addT;
        }
        count += duration;

        return count;
    }
};

414. 第三大的数 | 2022-12-5

//首次通过
#include<climits>
class Solution {
public:
    int thirdMax(vector<int>& nums) {
        int limitMin = INT_MIN;
        int maxs[3] = {limitMin, limitMin, limitMin};
        int count = 0;
        bool showMin = 0;
        for(auto num : nums){
            if(num == limitMin){
                showMin = 1;
            }
            bool equl = 0;
            for(int i = 0; i < 3; i++){
                if(num == maxs[i]){
                    equl = 1;
                }
            }
            if(equl == 1){
                continue;
            }
            if(num > maxs[2]){
                maxs[2] = num;
                count += 1;
            }
            int t = 0;
            if(maxs[0] < maxs[1]){
                t = maxs[0];  maxs[0] = maxs[1];  maxs[1] = t;
            }
            if(maxs[1] < maxs[2]){
                t = maxs[1];  maxs[1] = maxs[2];  maxs[2] = t;
            }
            if(maxs[0] < maxs[1]){
                t = maxs[0];  maxs[0] = maxs[1];  maxs[1] = t;
            }
        }
        int result = 0;
        if(showMin == 1 && count == 2){
            result = maxs[2];
        }
        else if(maxs[2] == limitMin){
            result = maxs[0];
        }
        else {
            result = maxs[2];
        }
        return result;
    }
};

628. 三个数的最大乘积 | 2022-12-6

想起了我们高数老师讲求函数的最值的时候，把所有可能的位置（极值和端点值）都列出来再进行比较就好了。

//首次通过
//56ms, 击败7.60%
#include<algorithm>
#include<cstdio>
using namespace std;
class Solution {
public:
    int maximumProduct(vector<int>& nums) {
        int numsSize = nums.size();
        int result = 0;
        int indexMid = -1;  //正负数交界处
        bool zeroShow = false;
        sort(nums.rbegin(), nums.rend());
        if(numsSize == 3){
            result = nums[0] * nums[1] * nums[2];
        }
        else{
            for(int i = 0; i <= numsSize-2; i++){
                if(nums[i] >= 0 && nums[i+1] < 0){
                    indexMid = i;
                    cout << nums[i] << endl;
                    break;
                }
            }
            vector<int> ts;
            if(nums[2] > 0){
                int t1 = nums[0] * nums[1] * nums[2];
                ts.push_back(t1);
            }
            if(nums[0] > 0 && nums[numsSize-2] < 0){
                int t2 = nums[0] * nums[numsSize-2] * nums[numsSize-1];
                ts.push_back(t2);
            }
            if(nums[1] > 0 && nums[numsSize-1] < 0){
                int t3 = nums[0] * nums[1] * nums[indexMid+1];
                ts.push_back(t3);
            }
            if(nums[numsSize-3] < 0){
                int t4 = nums[indexMid+1] * nums[indexMid+2] * nums[indexMid+3]; 
                ts.push_back(t4);
            }
            for(auto num : nums){
                if(num == 0){
                    zeroShow = true;
                }
            }
            if(zeroShow){
                ts.push_back(0);
            }
            result = *max_element(ts.begin(),ts.end()); 
        }
        return result;
    }
};

统计数组中的元素 645、697、448、442、41、274

645. 错误的集合 | 2022-12-6

借用了“桶排序”时的思路。

//首次通过
//28ms，击败71.37%
class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        int nSize = nums.size();
        vector<int> result;
        vector<bool> a(nSize+1, false);
        for(auto num : nums){
            if(a[num] == false){
                a[num] = true;
            }
            else{
                result.push_back(num);
            }
        }
        for(int i = 1; i <= nSize; i++){
            if(a[i] == false){
                result.push_back(i);
            }
        }
        return result;
    }
};

697. 数组的度 | 2022-12-6

对C++的语法不熟，写这个题时百度了好多次。此外，发现哈希表确实挺好用的。

//首次通过
//124ms，击败13.23%
#include<unordered_map>
using namespace std;
class Solution {
public:
    int findShortestSubArray(vector<int>& nums) {
        int nSize = nums.size();
        unordered_map<int, int> hash;  //统计频数
        for(auto num : nums){
            if(hash.count(num) == 0){
                hash[num] = 0;
            }
            hash[num] += 1;
        }
        int maxCount = 0;  //最大频数
        for(auto p : hash){
            if(p.second > maxCount){
                maxCount = p.second;
            }
        }
        vector<int> maxNum;  //频数最大的数
        for(auto p: hash){
            if(p.second == maxCount){
                maxNum.push_back(p.first);
            }
        }
        vector<int> diff;  //可能的子数组长度
        for(auto n : maxNum){
            int lIndex = find(nums.begin(), nums.end(), n) - nums.begin();  //find()的返回值不是int，但相减之后是
            int rIndex = nSize - 1 - (find(nums.rbegin(), nums.rend(), n) - nums.rbegin());
            cout << lIndex << ' ' << rIndex << endl;
            diff.push_back(rIndex - lIndex + 1);
        }
        int result = *min_element(diff.begin(), diff.end());
        return result;
    }
};

448. 找到所有数组中消失的数字 | 2022-12-6

力扣题解中一招“原地修改”确实秀到我了，不得不说差距客观存在，而且很大。

//首次通过
//96ms，击败12.45%
#include<unordered_map>
using namespace std;
class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        int nSize = nums.size();
        unordered_map<int, bool> hash;
        for(auto num : nums){
            if(hash.count(num) == 0){
                hash[num] = true;
            }
        }
        vector<int> result;
        for(int i = 1; i <= nSize; i++){
            if(hash[i] == 0){
                result.push_back(i);
            }
        }
        return result;
    }
};

442. 数组中重复的数据 | 2022-12-6

这题套用了第448题中官方题解中的原地修改法，在进行移植的时候也清晰了自己的理解。

//首次通过
//48ms，击败51.67%
class Solution {
public:
    vector<int> findDuplicates(vector<int>& nums) {
        int n = nums.size();
        for(auto& num : nums){
            int x = (num - 1) % n;
            nums[x] += n;
        }
        vector<int> ret;
        for(int i = 0; i < n; i++) {
            if(nums[i] > 2 * n){
                ret.push_back(i + 1);
            }
        }
        return ret;
    }
};

41. 缺失的第一个正数 | 2022-12-6

题目要求时间复杂度$O(n)$，空间复杂度$O(1)$。下面的代码因为新建了一个哈希表，所以空间复杂度为$O(n)$，不满足要求。

本题中$-2^{31}<=nums[i]<=2^{31}-1$，但看了题解发现还是可以将传入的nums改造为我们的哈希表。因为，如果设nums的长度为N，那么缺失的最小正整数一定在范围$[1,N+1]$内，因为N个数必然无法覆盖长度为N + 1的区间。

//首次通过
//76ms，击败10.85%
#include<climits>
using namespace std;
class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int nSize = nums.size();
        unordered_map<int, bool> hash;
        for(auto num : nums){
            if(hash.count(num) == 0){
                hash[num] = true;
            }
        }
        if(hash.count(1) == 0){
            return 1;
        }
        int minNum = INT_MAX;
        for(auto num : nums){
            int t1 = num;
            int t2 = num;
            if(t1 < INT_MAX){
                t1 += 1;
            }
            if(t2 > INT_MIN){
                t2 -= 1;
            }
            if(t1 > 0 && hash.count(t1) == 0){
                if(t1 < minNum){
                    minNum = t1;
                }
            }
            if(t2 > 0 && hash.count(t2) == 0){
                if(t2 < minNum){
                    minNum = t2;
                }
            }
        }
        return minNum;
    }
};

274. H 指数 | 2022-12-6

//首次通过
//0ms，击败100%
#include<algorithm>
using namespace std;
class Solution {
public:
    int hIndex(vector<int>& citations) {
        sort(citations.rbegin(), citations.rend());
        int cSize = citations.size();
        int result = 0;
        if(cSize == 1 && citations[0] >= 1){
            result = 1;
        }
        for(int i = 0; i <= cSize - 1; i++){
            if(i + 1 <= citations[i] && (i + 1 >= cSize || i + 1 >= citations[i+1])){
                result = i + 1;
                break;
            }
        }
        return result;
    }
};

数组的改变、移动 453、665、283

453. 最小操作次数使数组元素相等 | 2022-12-6

一开始我真没思路，看了题解才写出来。这题就非常体现了相对的思想，目标是相等，那么 n - 1 个数加一就相当于 1 个数减一。

//首次通过
//36ms，击败41.12%
class Solution {
public:
    int minMoves(vector<int>& nums) {
        int minNum = 1000000000;
        int count = 0;
        for(auto num : nums){
            if(num < minNum){
                minNum = num;
            }
        }
        for(auto num : nums){
            count += num - minNum;
        }
        return count;
    }
};

665. 非递减数列 | 2022-12-6

这段代码修修补补才终于通过，写得逻辑不太清晰，缩进数太多。有两种情况应该返回 false，

• 有多次下降（一次下降指出现一次$nums[i]>nums[i+1]$）
• 仅一次下降，但是处于特殊情况如下图，a 点高于下虚线，且 b 点低于上虚线。
  

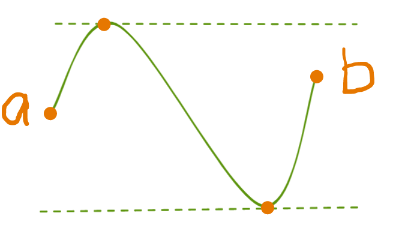
这题花时间较多，不太擅长分情况讨论。发现这个击败率是不稳定的，我刷新了几次，有一次击败了 98%，但是代码没改。

//首次通过
//20ms，击败79.55%
class Solution {
public:
    bool checkPossibility(vector<int>& nums) {
        int nSize = nums.size();
        int countDown = 0;
        bool result = true;
        if(nSize >= 3){
            for(int i = 0; i <= nSize - 3; i++){
                if(nums[i] > nums[i + 1]){
                    countDown += 1;
                    if(nums[i + 1] > nums[i + 2]){
                        result = false;
                    }
                    else if(i - 1 >= 0 && nums[i + 1] < nums[i - 1] && nums[i + 2] < nums[i]){
                        result = false;
                    }
                }
            }
            if(nums[nSize-2] > nums[nSize-1]){
                countDown += 1;
            }
            if(countDown > 1){
                result = false;
            }
        }
        return result;
    }
};

283. 移动零 | 2022-12-7

最初用的冒泡排序的思路，时间复杂度$O(n^2)$超时了，看了题解才写出来，时间复杂度变成了$O(n)$。

//首次通过
//16ms，击败88.55%
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int nSize = nums.size();
        int firstZero = -1;  //第一个0的位置
        int firstNum = -1;  //firstZero后面的第一个非零数的位置
        for(int i = 0; i < nSize; i++){
            if(firstZero == -1 && nums[i] == 0){
                firstZero = i;  
            }
            if(firstNum == -1 && firstZero != -1 && nums[i] != 0){
                firstNum = i;
                break;
            }
        }
        if(firstZero == -1 || firstNum == -1){
            return;
        }
        while(firstNum < nSize){
            if(nums[firstZero] == 0 && nums[firstNum] != 0){
                int t = nums[firstZero];  
                nums[firstZero] = nums[firstNum]; 
                nums[firstNum] = t;
            }
            firstZero += 1;
            while(firstNum < nSize && nums[firstNum] == 0){
                firstNum += 1;
            }
        }
        return;
    }
};

二维数组及滚动数组 118、119、661、598、419

118. 杨辉三角 | 2022-12-7

在考虑边界问题时脑袋常常容易混乱，又会犹豫是把边界情况单独处理，还是在形式上统一到普通情况中处理。

//首次通过
//0ms，击败100%
class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> a(numRows);
        a[0].push_back(1);
        for(int i = 1; i < numRows; i++){
            int nSize = a[i - 1].size();  //前一层的长度
            for(int j = 0; j < i + 1; j++){
                int num = 0;
                if(j < nSize){
                    num += a[i - 1][j];
                }
                if(j - 1 >= 0){
                    num += a[i - 1][j - 1];
                }
                a[i].push_back(num);
            }
        }
        return a;
    }
};

119. 杨辉三角 II | 2022-12-7

要得到第 n 行，只需先逐行求出前 n 行，然后返回时只返回最后一行就可以了。但有没有一种方法直接求第 n 行呢？

//首次通过
//0ms，击败100%
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        int numRows = rowIndex + 1;
        vector<vector<int>> a(numRows);
        a[0].push_back(1);
        for(int i = 1; i < numRows; i++){
            int nSize = a[i - 1].size();  //前一层的长度
            for(int j = 0; j < i + 1; j++){
                int num = 0;
                if(j < nSize){
                    num += a[i - 1][j];
                }
                if(j - 1 >= 0){
                    num += a[i - 1][j - 1];
                }
                a[i].push_back(num);
            }
        }
        return a[rowIndex];
    }
};

661. 图片平滑器 | 2022-12-7

多层循环嵌套遍历这我熟，嘿嘿。之前写过一个自动填数独的程序，可以看看，不回溯，试试候选数法1ms高效解数独谜题-C++实现。

//首次通过
//40ms，击败93.78%
class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
        int iSize = img.size();
        int jSize = img[0].size();
        vector<vector<int>> img_2(iSize, vector<int>(jSize));
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                int sum = 0;
                int count = 0;
                for(int m = i - 1; m <= i + 1; m++){
                    for(int n = j - 1; n <= j + 1; n++){
                        if(m >= 0 && n >=0 && m < iSize && n < jSize){
                            sum += img[m][n];
                            count += 1;
                        }
                    }
                }
                img_2[i][j] = sum / count;
            }
        }
        return img_2;
    }
};

598. 范围求和 II | 2022-12-7

//首次通过
//12ms，击败44.68%
class Solution {
public:
    int maxCount(int m, int n, vector<vector<int>>& ops) {
        int minM = 4*1e4, minN = 4*1e4;
        int result = 0;
        if(ops.size() == 0){
            return m * n;
        }
        for(auto op : ops){
            if(minM > op[0]){
                minM = op[0];
            }
            if(minN > op[1]){
                minN = op[1];
            }
        }
        return minM * minN;
    }
};

419. 甲板上的战舰 | 2022-12-7

题目的进阶要求是，只使用 $O(1)$ 额外空间，并且不修改 board 的值。下面的代码中修改 board 的值了。

//首次通过
//8ms，击败61.98%
class Solution {
public:
    int countBattleships(vector<vector<char>>& board) {
        int iSize = board.size();
        int jSize = board[0].size();
        int count = 0;
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(board[i][j] == 'X'){
                    count += 1;
                    for(int k = j + 1; k < jSize && board[i][k] == 'X'; k++){
                        board[i][k] = '.';
                    }
                    for(int k = i + 1; k < iSize && board[k][j] == 'X'; k++){
                        board[k][j] = '.';
                    }
                }
            }
        }
        return count;
    }
};

下面的代码是满足进阶要求的版本，遍历矩阵，以如下三种情况统计战舰数量：
1、单独的一个 X；
2、横向战舰左端点处的 X；
3、纵向战舰上端点处的 X。

using namespace std;
class Solution {
public:
    int countBattleships(vector<vector<char>>& board) {
        int iSize = board.size();
        int jSize = board[0].size();
        int count = 0;
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(board[i][j] == 'X'){
                    if((i-1 < 0 || board[i-1][j] == '.') && (i+1 < iSize && board[i+1][j] == 'X')){
                        count += 1;
                    }
                    else if((j-1 < 0 || board[i][j-1] == '.') && (j+1 < jSize && board[i][j+1] == 'X')){
                        count += 1;
                    }
                    else if((i-1 < 0 || board[i-1][j] == '.') && (i+1 >= iSize || board[i+1][j] == '.') && (j-1 < 0 || board[i][j-1] == '.') && (j+1 >= jSize || board[i][j+1] == '.')){
                        count += 1;
                    }
                }
            }
        }
        return count;
    }
};

数组的旋转 189、396

【精】189. 轮转数组 | 2022-12-7

冒泡的灵感，递归的思路，迭代的写法 （递归占用的栈空间应当也算程序的空间复杂度）。感觉这道题挺有意思，而且能自己写出来挺有成就感的，题解里好像没看到我一样的思路，不过他们的思路也很棒哈哈。我这还是相对复杂了一点。

简单介绍下思路吧。我们知道冒泡排序中，每次都是交换相邻的两个数字，而这里我们是不断地交换相邻的两个长为 k 的子数组。如下图所示，直到图中的最后 $k$ 个数字$[7,8,9]$冒到了最前面，我们就成功完成了轮转数组的任务。

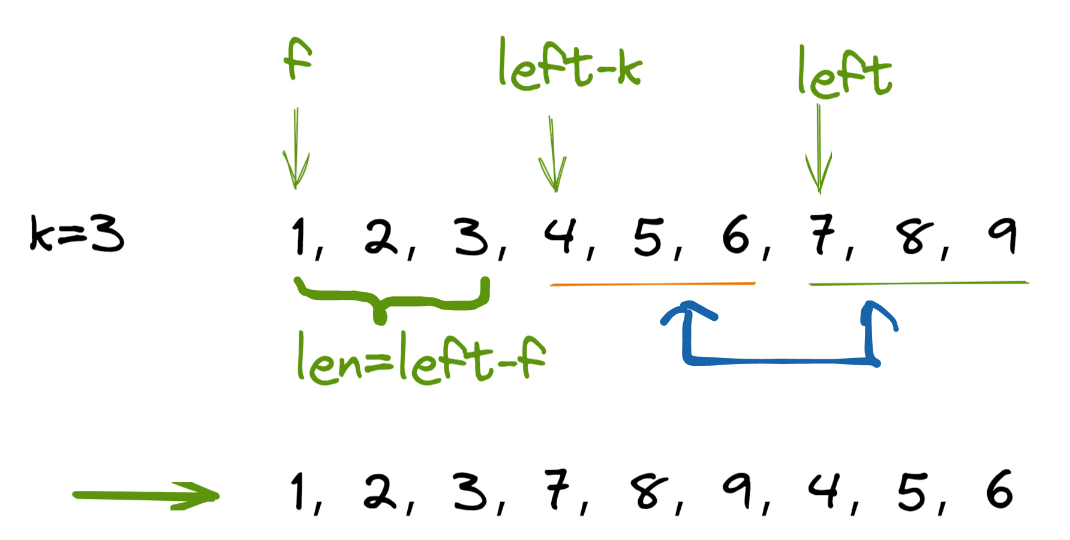
但是，当剩余的 $len$ 小于 $k$ 的时候怎么办呢？如下图，这时我们先交换一部分，然后更新 $k=k-len$，将剩下的 $[1,2,5,6]$，再看作原任务的一个子任务，递归求解。

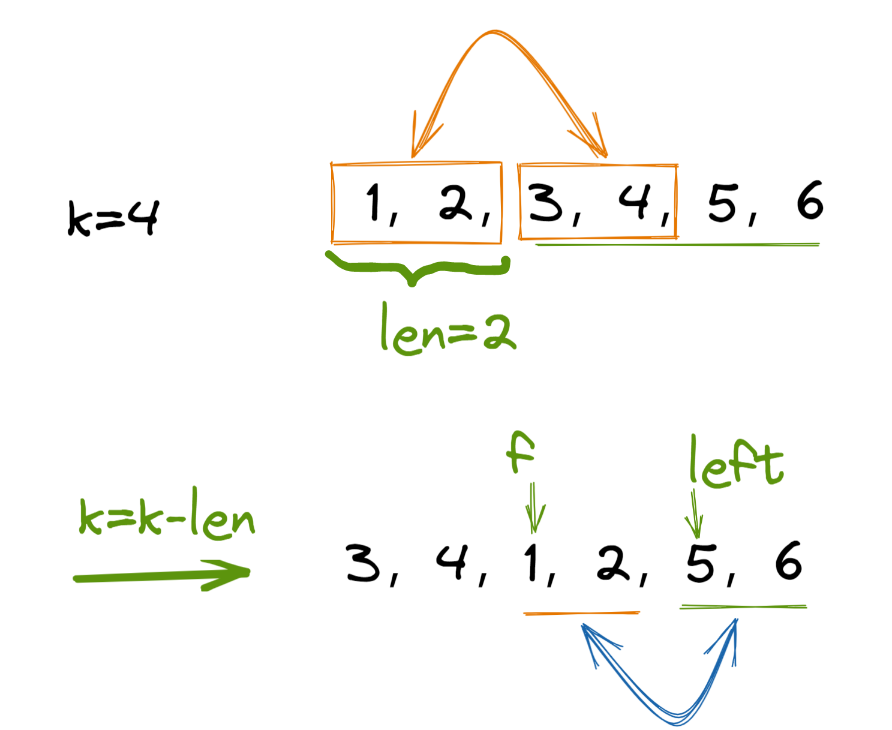
//修订
//24ms, 击败72.88%
using namespace std;
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int nSize = nums.size();
        k = k % nSize;  //移动nSize次就又回来了
        if(k == 0) { return; }
        int f = 0;
        int left = nSize - k;
        //f, left, k这3个变量控制递归状态
        while(f < left){
            int len = left - f;
            int a(0), b(0), m(0);
            if(len >= k){
                a = left - k;
                b = left;
                m = k;
                left = left - k;
            }
            else{
                a = f;
                b = f + len;
                m = len;
                k = k - len;
                f = f + len;
                left = f + len;
            }
            for(int i = 0; i < m; i++, a++, b++){
                swap(nums[a], nums[b]);
            }
        }
        return;
    }
};

如果讨厌太多行的代码，可以勉强挤成下面这样，但我不会建议你这样做，因为这几乎不会提高代码的可读性。

using namespace std;
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        k = k % nums.size();
        if(k == 0) { return; }
        int f = 0;
        int left = nums.size() - k;
        while(f < left){
            int len = left - f;
            int a = len >= k ? left - k : f;
            int b = len >= k ? left : f + len;
            int m = len >= k ? k : len;
            f = len >= k ? f : f + len;
            left = len >= k ? left - k : f + len;
            k = len >= k ? k : k - len;
            for(int i = 0; i < m; i++, a++, b++){
                swap(nums[a], nums[b]);
            }
        }
        return;
    }
};

396. 旋转函数 | 2022-12-7

关键在于想办法减少重复计算。

//首次通过，112ms，击败73.40%
class Solution {
public:
    int maxRotateFunction(vector<int>& nums) {
        int nSize = nums.size();
        vector<int> F;
        int f(0);
        for(int i = 0; i < nSize; i++){
            f += nums[i] * i;
        }
        F.push_back(f);
        int delta(0);
        for(int i = 0; i < nSize-1; i++){
            delta += nums[i];
        }
        delta -= nums[nSize-1] * (nSize-1);
        for(int i = nSize-1; i > 0; i--){
            f = f + delta;
            F.push_back(f);
            delta = delta + (nums[i] - nums[i-1]) * nSize;
        }
        int result = *max_element(F.begin(), F.end());
        return result;
    }
};

特定顺序遍历二维数组 54、59、498

54. 螺旋矩阵 | 2022-12-7

总想找到某种具有统一性的写法，以避免过多的分支结构。

//首次通过，0ms，击败100%
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> result;
        vector<int> deltaI = {0, 1, 0, -1};
        vector<int> deltaJ = {1, 0, -1, 0};
        int iSize = matrix.size();
        int jSize = matrix[0].size();
        int mSize = iSize * jSize;
        int null = 666;
        for(int count(0), state(0), i(0), j(0); count < mSize; count++, i += deltaI[state], j += deltaJ[state]){
            int iNext = i + deltaI[state];
            int jNext = j + deltaJ[state];
            if(iNext < 0 || iNext >= iSize || jNext < 0 || jNext >= jSize || matrix[iNext][jNext] == null){
                state = (state + 1) % 4;
            }
            result.push_back(matrix[i][j]);
            matrix[i][j] = null;
        }
        return result;
    }
};

59. 螺旋矩阵 II | 2022-12-8

只需在遍历螺旋矩阵的代码上稍作修改即可 。

//首次通过，0ms，击败100%
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> result(n, vector<int>(n));
        vector<int> deltaI = {0, 1, 0, -1};
        vector<int> deltaJ = {1, 0, -1, 0};
        int mSize = n * n;
        int null = 0;
        for(int count(0), state(0), i(0), j(0); count < mSize; count++, i += deltaI[state], j += deltaJ[state]){
            int iNext = i + deltaI[state];
            int jNext = j + deltaJ[state];
            if(iNext < 0 || iNext >= n || jNext < 0 || jNext >= n || result[iNext][jNext] != null){
                state = (state + 1) % 4;
            }
            result[i][j] = count + 1;
        }
        return result;
    }
};

498. 对角线遍历 | 2022-12-8

• 向右上时，如果走不了（会出界）就改为向右，还走不了就向下；
• 向左下时，如果走不了就改为向下，还走不了就向右。

//首次通过，16ms，击败98.43%
class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        vector<int> result;
        vector<int> deltaI = {-1, 1};
        vector<int> deltaJ = {1, -1};
        int iSize = mat.size();
        int jSize = mat[0].size();
        int mSize = iSize * jSize;
        for(int count(0), arrow(0), i(0), j(0); count < mSize; count++){
            result.push_back(mat[i][j]);
            int iNext = i + deltaI[arrow];
            int jNext = j + deltaJ[arrow];
            if(iNext >= 0 && iNext < iSize && jNext >= 0 && jNext < jSize){
                i = iNext;
                j = jNext;
            }
            else{
                if((arrow == 0 && j+1 < jSize) || (arrow == 1 && i+1 >= iSize)) 
                    j += 1;
                else 
                    i += 1;
                arrow = (arrow + 1) % 2;
            }
        }
        return result;
    }
};

二维数组变换 566、48、73、289

566. 重塑矩阵 | 2022-12-8

同步遍历两个矩阵即可。

//首次通过，8ms，86.60%
class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int iSize = mat.size();
        int jSize = mat[0].size();
        int Size = iSize * jSize;
        if(r * c != Size)
            return mat;
        vector<vector<int>> result(r, vector<int>(c));
        for(int i(0), j(0), m(0), n(0), count(0); count < Size; count++){
            result[m][n] = mat[i][j];
            i += (j+1) / jSize;
            j = (j+1) % jSize;
            m += (n+1) / c;
            n = (n+1) % c;
        }
        return result;
    }
};

48. 旋转图像 | 2022-12-8

有一段时间没有体会这种糟糕的编码体验了，4层的for循环和复杂的边界条件控制给我造成了很多麻烦。

• for循环1：控制矩阵的圈层，从外到里；
• for循环2：遍历当前圈层的一条边；
• for循环3：遍历当前边上一个点在四条边的对应点；
• for循环4：顺时针找下一个对应点。

后面两层循环其实可以省去，改成同时遍历一圈的4条边。

看力扣题解中另一种方法也不错，通过两次翻转即可。一次关于对角线镜像翻转；一次关于轴对称翻转。

//首次通过，0ms，击败100%
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        vector<int> deltaI = {0, 1, 0, -1};
        vector<int> deltaJ = {1, 0, -1, 0};
        for(int a(0), b(0), len(n); len > 0; a +=1, b += 1, len -= 2){
            for(int c(a), d(b); d < b + len - 1; d++){
                for(int i(c), j(d), t1(matrix[c][d]), count(0); count < 4; count++){
                    int iNext(i), jNext(j);
                    for(int k(0), state(count); k < len-1; k++){  //定位next
                        int iNNext = iNext + deltaI[state];
                        int jNNext = jNext + deltaJ[state];
                        if(iNNext < a || iNNext >= n-a || jNNext < a || jNNext >= n-a){
                            state = (state + 1) % 4;
                        }
                        iNext += deltaI[state];
                        jNext += deltaJ[state];
                    }
                    int t2 = matrix[iNext][jNext];
                    matrix[iNext][jNext] = t1;
                    t1 = t2;
                    i = iNext;
                    j = jNext;
                }
            }
        }
    }
};

73. 矩阵置零 | 2022-12-8

写完再看题目，发现下面代码使用的额外空间是 O(m+n)，而不是题目要求的 O(1)。

//首次通过，12ms，击败75.50%
class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int iSize = matrix.size();
        int jSize = matrix[0].size();
        vector<bool> r(iSize);
        vector<bool> c(jSize);
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(matrix[i][j] == 0){
                    r[i] = true;
                    c[j] = true;
                }
            }
        }
        cout << endl;
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(r[i] == true || c[j] == true){
                    matrix[i][j] = 0;
                }
            }
        }
    }
};

于是我重新得到了以下版本，

//20ms，击败8.60%
class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int iSize = matrix.size();
        int jSize = matrix[0].size();
        int a(0);
        int b(0);
        bool showZero(false);
        //找到一个0的位置，其所在行列被我们用来存放标记
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(matrix[i][j] == 0){
                    a = i;
                    b = j;
                    showZero = true;
                    break;
                }
            }
        }
        if(showZero == false){ return; }
        //将所在行和列不是0的元素标记为2，为后面排除原本存在的1的干扰
        for(int i = 0; i < iSize; i++){
            if(matrix[i][b] != 0){
                matrix[i][b] = 2;
            }
        }
        for(int j = 0; j < jSize; j++){
            if(matrix[a][j] != 0){
                matrix[a][j] = 2;
            }
        }
        //遍历矩阵，标记存在0的行和列
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(matrix[i][j] == 0){
                    matrix[i][b] = 1;
                    matrix[a][j] = 1;
                }
            }
        }
        //遍历矩阵，置零操作
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if((i != a && j != b) && (matrix[i][b] == 1 || matrix[a][j] == 1)){
                    matrix[i][j] = 0;
                }
            }
        }
        //将我们存放标记的行列也置零
        for(int i = 0; i < iSize; i++){
            matrix[i][b] = 0;
        }
        for(int j = 0; j < jSize; j++){
            matrix[a][j] = 0;
        }
    }
};

思维方向是可以的，即“改造原矩阵的一部分，作为我们存放标记的空间”，但这段代码在时间效率和代码简洁度上仍有较大的优化空间。但是，就这样吧，它已经满足题目要求了，哈哈。

289. 生命游戏 | 2022-12-9

为了实现原地算法，我们可以给细胞引入两个额外的状态，即包含过程信息的状态。

//首次通过，0ms，击败100%
class Solution {
public:
    void gameOfLife(vector<vector<int>>& board) {
        const int oldDie = 2;  //初始状态是死细胞，下一个状态会复活
        const int oldLive = 3;  //初始状态是活细胞，下一个状态会死
        int iSize = board.size();
        int jSize = board[0].size();
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                int count = 0;
                for(int m = i-1; m <= i+1; m++){
                    for(int n = j-1; n <= j+1; n++){
                        if((m >= 0 && m < iSize && n >=0 && n <jSize) && (m != i || n != j) && (board[m][n] == 1 || board[m][n] == oldLive)){
                            count += 1;
                        }
                    }
                }
                if(board[i][j] == 1 && (count < 2 || count > 3)){
                    board[i][j] = oldLive;
                }
                else if(board[i][j] == 0 && count == 3){
                    board[i][j] = oldDie;
                }
            }
        }
        for(int i = 0; i < iSize; i++){
            for(int j = 0; j < jSize; j++){
                if(board[i][j] == oldDie){
                    board[i][j] = 1;
                }
                if(board[i][j] == oldLive){
                    board[i][j] = 0;
                }
            }
        }
    }
};

前缀和数组 303、304、238

303. 区域和检索 - 数组不可变 | 2022-12-9

//首次通过，260ms，击败13.75%
class NumArray {
public:
    vector<int> numS;
    NumArray(vector<int>& nums) {
        numS = nums;
    }
    
    int sumRange(int left, int right) {
        int sum(0);
        for(int i = left; i <= right; i++){
            sum += numS[i];
        }
        return sum;
    }
};

可我没想到，大家面对简单题也在重拳出击。下面是利用前缀和的解法，将单次查询中的时间复杂度优化到了 O(1)。

//优化，20ms，击败80.16%
class NumArray {
public:
    vector<int> sums;
    NumArray(vector<int>& nums) {
        int nSize = nums.size();
        sums.push_back(nums[0]);
        for(int i = 1; i < nSize; i++){
            sums.push_back(sums[i-1] + nums[i]);
        }
    }
    
    int sumRange(int left, int right) {
        int sum = 0;
        sum = sums[right] - (left > 0 ? sums[left - 1] : 0);
        return sum;
    }
};

304. 二维区域和检索 - 矩阵不可变 | 2022-12-9

从一维到二维的升级版，思路相似。这题因为对二维的vector不熟，卡了一会儿；此外就是折磨人的边界问题。

//首次通过，324ms，击败89.77%
class NumMatrix {
public:
    vector<vector<int>> sums;
    NumMatrix(vector<vector<int>>& matrix) {
        int iSize = matrix.size();
        int jSize = matrix[0].size();
        for(int i = 0; i < iSize; i++){
            sums.push_back(vector<int>(0));
            for(int j = 0; j < jSize; j++){
                int A = i > 0 ? sums[i-1][j] : 0;
                int B = j > 0 ? sums[i][j-1] : 0;
                int C = i > 0 && j > 0 ? sums[i-1][j-1] : 0;
                int sum = matrix[i][j] + A + B - C;
                sums[i].push_back(sum);
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        int all = sums[row2][col2];
        int A = row1 > 0 ? sums[row1-1][col2] : 0;
        int B = col1 > 0 ? sums[row2][col1-1] : 0;
        int C = row1 > 0 && col1 > 0 ? sums[row1-1][col1-1] : 0;
        int sum = all - A - B + C;
        return sum;
    }
};

238. 除自身以外数组的乘积 | 2022-12-9

别人怎么可以这么聪明？这题我没写出来，摸到了窗户纸，但就是没捅破。

一个基本是思路是，三次遍历数组，

• 第一次正向遍历，计算从第一个数到当前位置的区间内，所有数字的乘积，放入一个数组 A；
• 第二次反向遍历，计算从最后一个数到当前位置的区间内，所有数字的乘积，放入另一个数组 B；
• 第三次随便遍历，answer[i] = A[i-1] * B[i+1]。

基于上述思路进行改进，我们可以用输出数组answer作为数组B，然后第三次遍历进行正向遍历，而A则可以随着遍历过程动态生成，得到了以下代码。

//首次通过，20ms，击败73.59%
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int nSize = nums.size();
        vector<int> out(nSize);
        out[nSize-1] = nums[nSize-1];
        for(int i = nSize-2; i >= 0; i--){
            out[i] = out[i+1] * nums[i];
        }
        for(int i = 0, product = 1; i < nSize; i++){
            int A = product;
            int B = i < nSize-1 ? out[i+1] : 1;
            out[i] = A * B;
            product *= nums[i];
        }
        return out;
    }
};

---

敬请期待下一节——字符串。