原文(附文献下载)
1 群体智能优化算法
SI(swarm intelligence)系统的特点是个体间的相互作用促进了智能行为的出现。
SI优化过程的实现主要包括以下两个步骤:
- 在搜索空间范围内创建一组随机个体
- 在迭代过程中组合、移动或进化这些随机个体。
每种优化算法的区别在于如何在优化过程中设计新的策略(特别是组合、移动或进化),如:
- 粒子群优化算法:在进化过程中,每个个体的位置可以逐渐收敛到全局最优解,主要取决于以下两个重要位置:1)一个是每个个体的最优位置,2)另一个是整个种群的全局最优位置。
- 蚁群优化(ant colony optimization, ACO)算法:在算法中,每只蚂蚁的路径表示一个可行解,所有蚂蚁的路径构成解空间。信息素的选择对于蚁群在整个优化问题空间中搜索全局最优路径至关重要。在这种情况下,在信息素水平较强的方向上获得最短路径。
除了研究群体与个体之间的关系,新的SI还研究了生物的习性。如:
- 灰狼优化(GWO)算法:该算法模拟了灰狼的领导等级(包括alpha、beta、delta和omega)和狩猎行为。GWO算法的狩猎机制主要包括搜索、包围和攻击猎物。
- 鲸鱼优化算法(WOA):首次提出了模仿座头鲸社会行为的气泡网捕猎策略。
除了以上介绍的算法,还有很多算法,且都应用到了实践中,但根据No Free Lunch (NFL)定理,我们知道没有一个算法可以处理所有的优化问题。
换句话说,一个算法的优化性能可能在一组问题中表现良好,而在另一组问题中表现不佳。
因此,NFL定理鼓励寻找和开发更多性能令人满意的优化器。在上述讨论的基础上,作者提出了一种新的基于SI的优化技术-蜣螂算法(Dung beetle optimizer,DBO),旨在为复杂的优化问题提供一种更高效的优化器。
2 蜣螂的生活习性
蜣螂以动物的粪便为食。研究表明,屎壳郎有一个有趣的习惯,就是把粪便打成球状,然后滚出来,如图所示。

滚球

向后滚
其会尽可能快速有效地移动它们的粪球,这可以防止它们与其他屎壳螂竞争(偷窃)。

偷窃/竞争
另一方面,屎壳郎是利用天体线索(特别是太阳、月亮和偏振光)来导航,使粪球沿直线滚动。如果完全没有光源(即完全黑暗),屎壳郎的路径就不再是直线,而是弯曲的,有时甚至略圆。
一些自然因素(如风和不平整的地面)也会导致屎壳郎偏离原来的方向。此外,屎壳郎在滚动过程中很可能会遇到障碍物,无法前进。在这方面,蜣螂通常爬到粪球上跳舞(包括一系列的旋转和停顿),这决定了它们的运动方向。

跳舞(旋转和停顿)
蜣螂另一个有趣的行为是,获得的粪球有以下两个主要目的:
- 一些粪球用来产卵和养育下一代
- 其余的用作食物。
具体来说,蜣螂把粪球埋起来,雌性蜣螂在这些粪球里产卵。

埋球

繁殖(产卵)

繁殖(养育)
粪球不仅是幼虫的发育场所,还为幼虫提供了生活所必需的食物。因此,粪球对屎壳郎的生存起着不可替代的作用。
基于屎壳郎的滚球、跳舞、觅食、偷窃和繁殖行为提出了DBO算法。
3 数学模型
1) 模拟滚球行为
根据上面的讨论,我们知道蜣螂在滚动过程中需要通过天体线索来导航,以保持粪球在直线上滚动。
为了模拟滚动球的行为,蜣螂需要在整个搜索空间中朝着给定的方向移动。
屎壳郎的运动轨迹如图所示。在这张图中,可以看到屎壳郎利用太阳导航,红色箭头表示滚动方向。
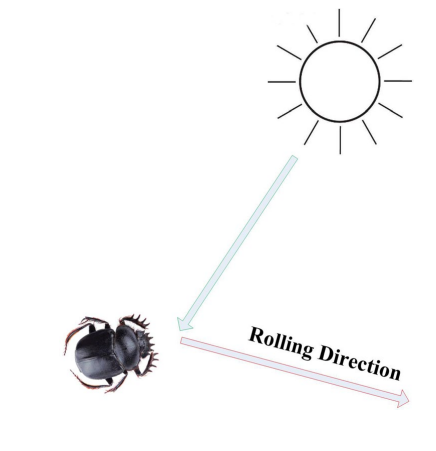
运动轨迹
在本文中,假设光源的强度也会影响屎壳郎的路径。在滚球过程中,滚球屎壳郎的位置被更新,可表示为:
x i ( t + 1 ) = x i ( t ) + α × k × x i ( t − 1 ) + b × Δ x , ( 式 1 ) Δ x = ∣ x i ( t ) − X w ∣ \begin{aligned} x_{i}(t+1) & =x_{i}(t)+\alpha \times k \times x_{i}(t-1)+b \times \Delta x, \quad (式1)\\ \\ \Delta x & =\left|x_{i}(t)-X^{w}\right| \end{aligned} xi(t+1)Δx=xi(t)+α×k×xi(t−1)+b×Δx,(式1)=∣xi(t)−Xw∣
式中:
t表示当前迭代次数-
x
i
(
t
)
x_{i}(t)
xi(t) 表示第
i只蜣螂在第t次迭代时的位置信息 k∈(0,0.2)表示一个常值,表示缺陷系数b表示属于(0,1)的常值-
α
\alpha
α 是赋值为
-1或1的自然系数 - X w X^{w} Xw 表示全局最差位置
- Δ x \Delta x Δx 用来模拟光强的变化
选择两个参数(k和b)的合适值是至关重要的,本文中k和b分别设为0.1和0.3。
α \alpha α 意味着许多自然因素(如风和不平整的地面)可以使屎壳郎偏离原来的方向。其中, α \alpha α= 1表示无偏差, α \alpha α=−1表示偏离原方向。
为了模拟现实世界中的复杂环境,本文通过概率法将 α \alpha α设为1或-1。

同样, Δ x \Delta x Δx 值越高,光源越弱。其具有以下两个优点:
- 在优化过程中尽可能彻底地探索整个问题空间
- 追求更强的搜索性能,减少陷入局部最优的可能性。
因此, X w X^{w} Xw 更适合控制 Δ x \Delta x Δx 的值来扩大搜索范围。
当屎壳郎遇到障碍无法前进时,它需要通过舞蹈来重新定位,以获得新的路线。
2) 模拟跳舞行为
为了模拟舞蹈行为,我们使用切线函数来得到新的滚动方向。
我们只需要考虑在区间 [ 0 , π ] [0,\pi] [0,π]上定义的正切函数的值,如图所示。

一旦蜣螂成功地确定了一个新的方向,它应该继续向后滚动球。因此,对滚球屎壳郎的位置进行更新和定义如下:
x i ( t + 1 ) = x i ( t ) + tan ( θ ) ∣ x i ( t ) − x i ( t − 1 ) ∣ ( 式 2 ) x_{i}(t+1)=x_{i}(t)+\tan (\theta)\left|x_{i}(t)-x_{i}(t-1)\right| \quad (式2) xi(t+1)=xi(t)+tan(θ)∣xi(t)−xi(t−1)∣(式2)
- θ ∈ [ 0 , π ] \theta\in[0,\pi] θ∈[0,π]:偏转角。
-
∣
x
i
(
t
)
−
x
i
(
t
−
1
)
∣
\left|x_{i}(t)-x_{i}(t-1)\right|
∣xi(t)−xi(t−1)∣:第
i只蜣螂在第t次迭代时的位置与第t - 1次迭代时的位置之差。因此,滚球屎壳郎的位置更新与当前和历史信息密切相关。
如果 θ \theta θ 等于0, θ / 2 \theta/2 θ/2或 θ \theta θ,屎壳郎的位置不会更新。

蜣螂会将粪球滚到安全的地方,并将粪球藏起来(见下图)。为了给后代提供一个安全的环境,选择合适的产卵地点对蜣螂来说至关重要。
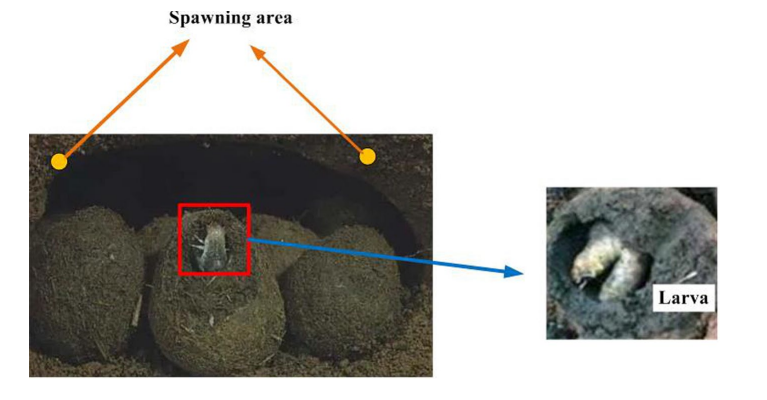
3) 模拟产卵行为
在上述讨论的启发下,提出了一种边界选择策略来模拟雌性蜣螂产卵的区域,其定义为:
L b ∗ = max ( X ∗ × ( 1 − R ) , L b ) , U b ∗ = min ( X ∗ × ( 1 + R ) , U b ) ( 式 3 ) \begin{array}{l} L b^{*}=\max \left(X^{*} \times(1-R), L b\right), \\ \\ U b^{*}=\min \left(X^{*} \times(1+R), U b\right) \end{array}\quad (式3) Lb∗=max(X∗×(1−R),Lb),Ub∗=min(X∗×(1+R),Ub)(式3)
- X ∗ X^{*} X∗ 表示当前局部最佳位置
- L b ∗ L b^{*} Lb∗和 U b ∗ U b^{*} Ub∗ 分别表示产卵区下限和上限
- R = 1 − t / T m a x R = 1−t/T_{max} R=1−t/Tmax, T m a x T_{max} Tmax 表示最大迭代次数
- L b Lb Lb 和 U b Ub Ub 分别表示优化问题的下限和上限
如图所示,当前局部最佳位置 X ∗ X^{*} X∗ 用一个大棕色圆圈表示,而 X ∗ X^{*} X∗ 周围的小黑圆圈表示卵球。每个卵球包含一个屎壳螂卵。红色小圆圈代表边界的上下边界。


产卵区
一旦确定了产卵区域,雌性蜣螂就会选择这个区域的卵球产卵。对于DBO算法,每只雌性蜣螂在每次迭代中只产一个卵。
由(3)可以清楚地看到,产卵区边界范围是动态变化的,主要由R值决定。
因此,在迭代过程中巢球的位置也是动态的:
B i ( t + 1 ) = X ∗ + b 1 × ( B i ( t ) − L b ∗ ) + b 2 × ( B i ( t ) − U b ∗ ) ( 式 4 ) B_{i}(t+1)=X^{*}+b_{1} \times\left(B_{i}(t)-L b^{*}\right)+b_{2} \times\left(B_{i}(t)-U b^{*}\right) \quad (式4) Bi(t+1)=X∗+b1×(Bi(t)−Lb∗)+b2×(Bi(t)−Ub∗)(式4)
-
B
i
(
t
)
B_{i}(t)
Bi(t) 为第
i个球在第t次迭代时的位置信息 -
b
1
b_1
b1 和
b
2
b_2
b2 为两个大小为
1 × D的独立随机向量 D为优化问题的维数
注意窝球的位置被严格限制在一定范围内,即产卵区域。

4) 模拟觅食行为
一些成年屎壳郎从地下钻出来觅食。本文称其为小屎壳郎。此外,需要建立最佳觅食区域来引导甲虫觅食,如下图所示。

最优觅食区域的边界定义如下:
L b b = max ( X b × ( 1 − R ) , L b ) U b b = min ( X b × ( 1 + R ) , U b ) ( 式 5 ) \begin{array}{l} L b^{b}=\max \left(X^{b} \times(1-R), L b\right) \\ \\ U b^{b}=\min \left(X^{b} \times(1+R), U b\right) \end{array} \quad (式5) Lbb=max(Xb×(1−R),Lb)Ubb=min(Xb×(1+R),Ub)(式5)
- X b X^{b} Xb 为全局最佳位置
- L b Lb Lb 和 U b Ub Ub 分别为最佳觅食区域的下界和上界,其他参数在 (3) 中定义。
因此,小蜣螂的位置更新如下:
x i ( t + 1 ) = x i ( t ) + C 1 × ( x i ( t ) − L b b ) + C 2 × ( x i ( t ) − U b b ) ( 式 6 ) x_{i}(t+1)=x_{i}(t)+C_{1} \times\left(x_{i}(t)-L b^{b}\right)+C_{2} \times\left(x_{i}(t)-U b^{b}\right) \quad (式6) xi(t+1)=xi(t)+C1×(xi(t)−Lbb)+C2×(xi(t)−Ubb)(式6)
-
x
i
(
t
)
x_{i}(t)
xi(t) 为第
i只小蜣螂在第t次迭代时的位置信息 - C 1 C_1 C1 为服从正态分布的随机数
-
C
2
C_2
C2 为属于
(0,1)的随机向量
5) 模拟偷窃行为
一些屎壳郎,被称为小偷,从其他屎壳郎那里偷粪球(见下图),需要指出的是,这是自然界中很常见的现象。

此外,由 (5) 可以看出, X b X^{b} Xb 是最佳食物来源。因此,可以假设 X b X^{b} Xb 附近是最适合竞争食物的地方。在迭代过程中,小偷的位置信息被更新:
x i ( t + 1 ) = X b + S × g × ( ∣ x i ( t ) − X ∗ ∣ + ∣ x i ( t ) − X b ∣ ) x_{i}(t+1)=X^{b}+S \times g \times\left(\left|x_{i}(t)-X^{*}\right|+\left|x_{i}(t)-X^{b}\right|\right) xi(t+1)=Xb+S×g×(∣xi(t)−X∗∣+∣∣xi(t)−Xb∣∣)
-
x
i
(
t
)
x_{i}(t)
xi(t) 为第
i个小偷在第t次迭代时的 x i ( t ) x_{i}(t) xi(t) g为服从正态分布的大小为1 × D的随机向量,S为常数值
4 算法框架
基于以上讨论,本文提出的DBO算法的伪代码如下所示。

- 首先,设 T m a x T_{max} Tmax 为最大迭代次数, N N N为总体大小。
- 然后对DBO算法的所有代理进行随机初始化,其分布设置如下图所示。
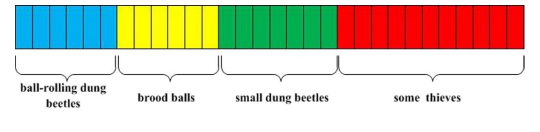
在这个图形中,小矩形的数量表示总体大小。假设总体规模为30:蓝色、黄色、绿色和红色的长方形分别代表滚球的屎壳郎、窝球、小屎壳郎和小偷。
- 之后,根据步骤2-27,知道了滚球屎壳郎、窝球、小屎壳郎和小偷在优化过程中不断更新。
- 最后输出最佳位置 X b X^{b} Xb 及其适应度值。
综上所述,对于任意优化问题,DBO算法作为一种新型的基于SI的优化技术,主要有六个步骤,可以概括为:
- 初始化屎壳郎群和DBO算法参数
- 根据目标函数计算各agent的适应度值
- 更 新所有屎壳郎的位置
- 判断各agent是否出界
- 更新当前最优解及其适应度值
- 重复上述步骤,直到
t满足终止准则,输出全局最优解及其适应度值
5 总结
DBO算法在收敛速度、求解精度和稳定性方面与其他7种优化技术进行了比较,显示出具有竞争力的搜索性能。
从理论上讲,DBO算法在探索或开发方面比其他算法更具竞争力的原因有以下几个特点:
- 提出了一种新型的滚球蜣螂搜索机制,不同的搜索模式使我们可以:A) 利用不同时间段的信息对搜索空间进行彻底的探索;b) 追求更强的搜索能力,以避免陷入局部最优。
- R参数具有动态变化的特点,可以进一步激发DBO算法的探索和开发状态。
- 不同的区域搜索策略(包括产卵区域和最佳觅食区域)可以促进DBO算法的利用行为。
- 不同的更新规则可以保证所开发的DBO算法在局部和全局搜索能力之间保持足够的平衡。
matlab code:
https://www.mathworks.com/matlabcentral/fileexchange/121278-dung-beetle-optimizer-dbo
参考:
Xue, J., Shen, B. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization. J Supercomput (2022). https://doi.org/10.1007/s11227-022-04959-6.