翻译：

给定两个数组𝑎和𝑏，长度都为𝑛。

选择索引𝑖(1≤𝑖≤𝑛)，将𝑎𝑖和𝑏𝑖交换。

让我们来定义数组的成本𝑎作为∑𝑛𝑖= 1∑𝑛𝑗=𝑖+ 1(𝑎𝑖+𝑎𝑗)2。同样,数组𝑏成本∑𝑛𝑖= 1∑𝑛𝑗=𝑖+ 1(𝑏𝑖+𝑏𝑗)2。

您的任务是最小化两个数组的总开销。

输入
每个测试用例由几个测试用例组成。第一行包含一个整数𝑡(1≤𝑡≤40)——测试用例的数量。下面是输入数据集的描述。

每个测试用例的第一行包含一个整数𝑛(1≤𝑛≤100)——两个数组的长度。

每个测试用例的第二行包含𝑛整数𝑎1，𝑎2，…，𝑎𝑛(1≤𝑎𝑖≤100)-第一个数组的元素。

每个测试用例的第三行包含𝑛整数𝑏1，𝑏2，…，𝑏𝑛(1≤𝑏𝑖≤100)-第二个数组的元素。

可以保证所有测试用例中𝑛的总和不超过100。

输出
对于每个测试用例，打印可能的最小总成本。

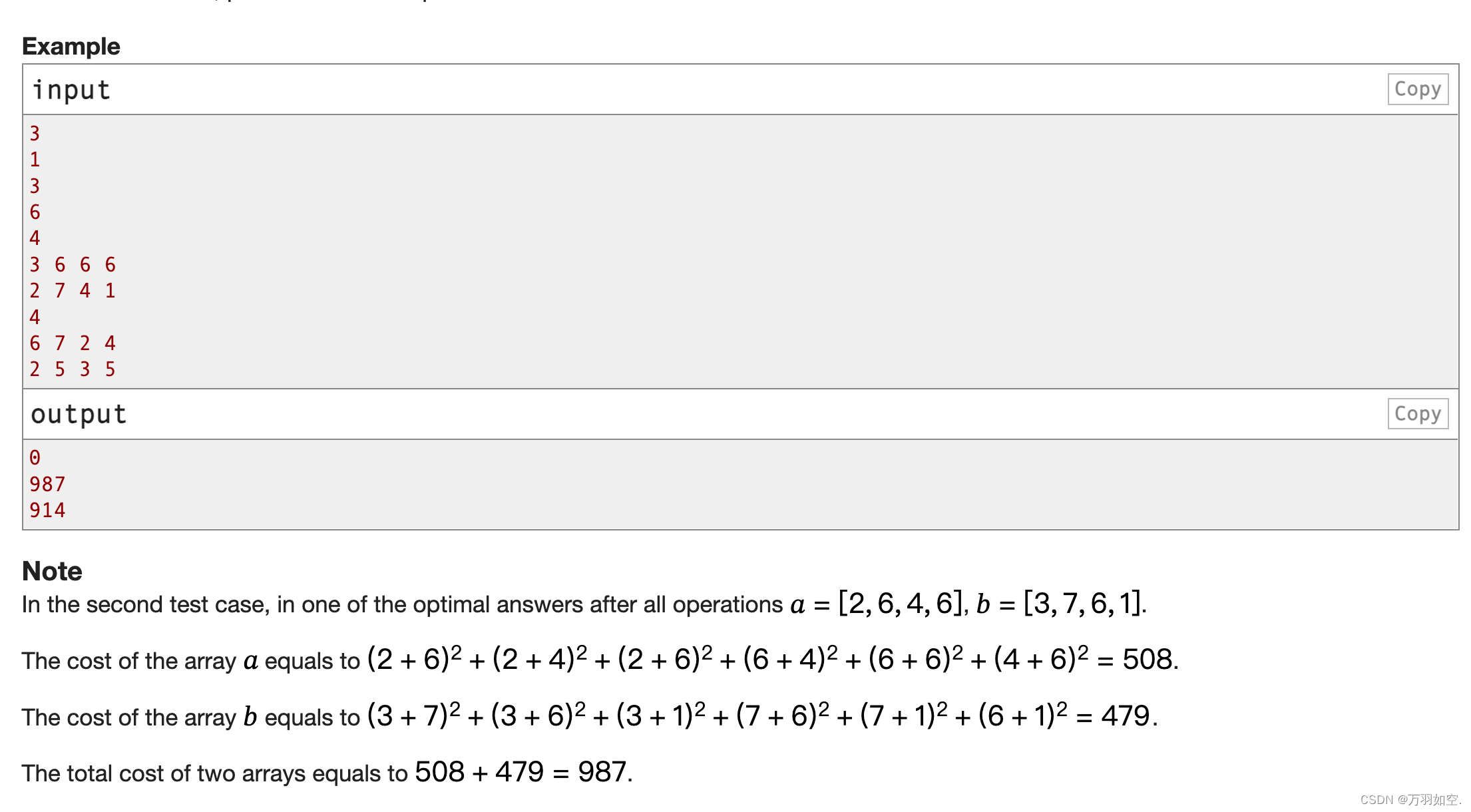
例子
inputCopy
3.
1
3.
6
4
3 6 6 6
2 7 4 1
4
6 7 2 4
2 5 3 5
outputCopy
0
987
914
请注意
在第二个测试用例中，在所有操作后的一个最优答案𝑎=[2,6,4,6]，𝑏=[3,7,6,1]。

数组的成本𝑎等于(2 + 6)2 +(2 + 4)2 +(2 + 6)2 + 2(6 + 4)+(6 + 6)2 +(4 + 6)2 = 508。

数组的成本𝑏等于(3 + 7)2 +(3 + 6)2 +(3 + 1)2 + 2(7 + 6)+(7 + 1)2 + 2 = 479(6 + 1)。

两个数组的总开销等于508+479=987。

思路：

我们先将式子展开，我们可以看出来有些总和是固定的，(n-1)ai^2,bi也是类似，然后之后不同的就是 2*ai*aj，2*bi*bj。所以我们只需要考虑让后面这些最小即可，同下标下，可以随意变换，所以我们可以用分组背包来拿，每次拿第一个或者拿第二个，最后根据每个总和的值来枚举，取最小值。因为没有列式子所以可能听起来有些不懂，可以自己手动列一下一个数组的成本，大概就懂了。

嗲吗：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
int a[105],b[105];
bool dp[105][100005];
ll sum=0;
ll na=0;
ll cxk=0;
void solv(){
    cin>>n;
    sum=0;
    na=0;
    cxk=0;
    for (int i=1; i<=n; i++) {
        cin>>a[i];
        cxk+=(n-2)*a[i]*a[i];
        sum+=a[i];
    }
//    printf("%lld\n",cxk);
    for (int i =1; i<=n; i++) {
        cin>>b[i];
        cxk+=(n-2)*b[i]*b[i];
        sum+=b[i];
    }
    if (n==1) {
        printf("0\n");return;
    }
    for (int i=1; i<=n; i++) {
        for (int j =0; j<=sum; j++) {
            dp[i][j]=false;
        }
    }
    dp[0][0]=true;
    for (int i =1; i<=n; i++) {
        for (int j =sum; j>=0; j--) {
            if (j>=a[i]&&dp[i-1][j-a[i]]) {
                dp[i][j]|=dp[i-1][j-a[i]];
            }
            
            if (j>=b[i]&&dp[i-1][j-b[i]]) {
                dp[i][j]|=dp[i-1][j-b[i]];
            }
        }
    }
//    for (int i =1; i<=n; i++) {
//        for (int j =0; j<=sum; j++) {
//            printf("%d ",dp[i][j]);
//        }printf("\n");
//    }
    ll lq=1e17+5;
//    printf("%lld\n",cxk);
    for (int i =0; i<=sum; i++) {
        if (dp[n][i]) {
            lq=min(lq,i*i+(sum-i)*(sum-i));
        }
    }
    
    printf("%lld\n",lq+cxk);
    
    
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}