LeetCode HOT 100 —— 207 .课程表

news2024/9/24 15:18:32

题目

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

在这里插入图片描述

思路

拓扑排序：

用有向图表示依赖关系：

示例：n = 6，先决条件表：[[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
课 0, 1, 2 没有先修课，可以直接选。其余的课，都有两门先修课
用有向图来表示依赖关系：
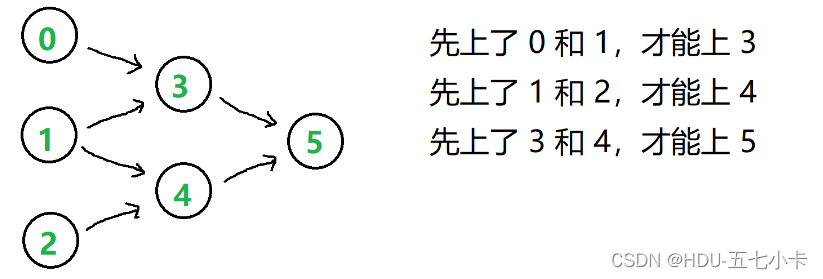
上图是一个有向无环图，把一个 有向无环图 转成 线性的排序 就是 拓扑排序
有向图中有入度和出度两个概念，在本例中，顶点 0、1、2 的入度为 0，顶点 3、4、5 的入度为 2

选课顺序：

每次只能选入度为0的课，因为它不依赖别的课，如选了0，课3的入度由 2 变 1，接着选1，课 3 的入度变 0，课 4 的入度由 2 变 1，接着选 2，课 4 的入度变 0

然后现在，课 3 和课 4 的入度都为 0，继续选入度为 0 的课……直到选不到入度为 0 的课

类似BFS的思想：

让入度为 0 的课入队列，它们是能直接选的课
然后逐个出队列，出队列代表着该课被选，需要减小相关课（依赖出队列课的课）的入度
如果相关课的入度新变为 0，安排它入队列、再出队列……直到没有入度为 0 的课可入队列

所需的数据结构：

入度数组：课程号0到n-1作为索引，通过遍历先决条件表求出对应的初始入度
邻接表：用哈希表记录依赖关系
（1）key：课号
（2）value: 依赖这门课的后续课（数组）

判断是否修完所有课程：

BFS结束时，如果仍有课的入度不为0，无法被选，就无法完成所有课程
或者用一个变量count记录入队列的顶点个数，判断最后count是否等于总课程数

java代码如下：

class Solution{
	// 节点的入度: 使用数组保存每个节点的入度
	public boolean canFinish(int numCourses, int[][] prerequisites){
		// 1.课号和对应的入度
		Map<Integer,Integer> inDegree = new HashMap<>();
		// 将所有的课程先放入
		for(int i = 0; i < numCourses; i++){
			inDegree.put(i,0);
		}
		// 2.依赖关系, 依赖当前课程的后序课程
		Map<Integer,List<Integer>> adj = new HashMap<>();
		
		//初始化入度和依赖关系
		for(int[] relate : prerequisites){//prerequisites里面是一个数组列表，每个元素就是一个int[]数组
			// (3,0), 想学3号课程要先完成0号课程, 更新3号课程的入度和0号课程的依赖(邻接表),即next依赖于cur
			int cur = relate[1];//需要先学习的前驱课程，相当于(3,0)的0
			int next = relate[0];//完成前驱课程之后才能学习的课程，相当于(3,0)的3
			// 1.更新入度,因为next依赖于cur，所以增加入度
			inDegree.put(next,inDegree.get(next) + 1);
			// 2.当前节点的邻接表
			if(!adj.containsKey(cur)){//如果不包括前驱课程
				adj.put(cur, new ArrayList<>());//更新依赖图
			}
			adj.get(cur).add(next);//因为next依赖于cur，所以添加依赖关系
		}
		
		//3.BFS, 将入度为0的课程放入队列, 队列中的课程就是可以直接学的课程
		Queue<Integer> q = new LinkedList<>();
		for(int key : inDegree.keySet()){
			if(inDegree.get(key) == 0){
				q.offer(key);
			}
		}
		// 取出一个节点, 对应学习这门课程
		// 遍历当前邻接表, 更新其入度; 更新之后查看入度, 如果为0, 加入到队列
		while(!q.isEmpty()){
			int cur = q.poll();
			// 遍历当前课程的邻接表, 更新后继节点的入度
			if(!adj.containsKey(cur)){
				continue;
			}
			List<Integer> successList = adj.get(cur);//返回的是依赖于cur的数组列表
			
			for(int k : successList){//遍历这个列表，里面所有的入度减少一
				inDegree.put(k, inDegree.get(k) - 1);
				if(inDegree.get(k) == 0){//如果发现有入度为0的，则入队列
					q.offer(k);
				}
			}
		}
		
		// 4.遍历入队, 如果还有课程的入度不为0, 返回fasle
		for(int key : inDegree.keySet()){
			if(inDegree.get(key) != 0){
				return false;
			}
		}
		return true;
	}
}