基本知识

01背包

二维，两层for循环的循序，物品和背包不重要。
$dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])$; 递归公式中可以看出$dp[i][j]$是靠$dp[i-1][j]$和$dp[i-1][j-weight[i]]$推导出来的。
一维滚动数组，只能先物品后背包

完全背包

这个视频讲了完全背包和01背包的区别

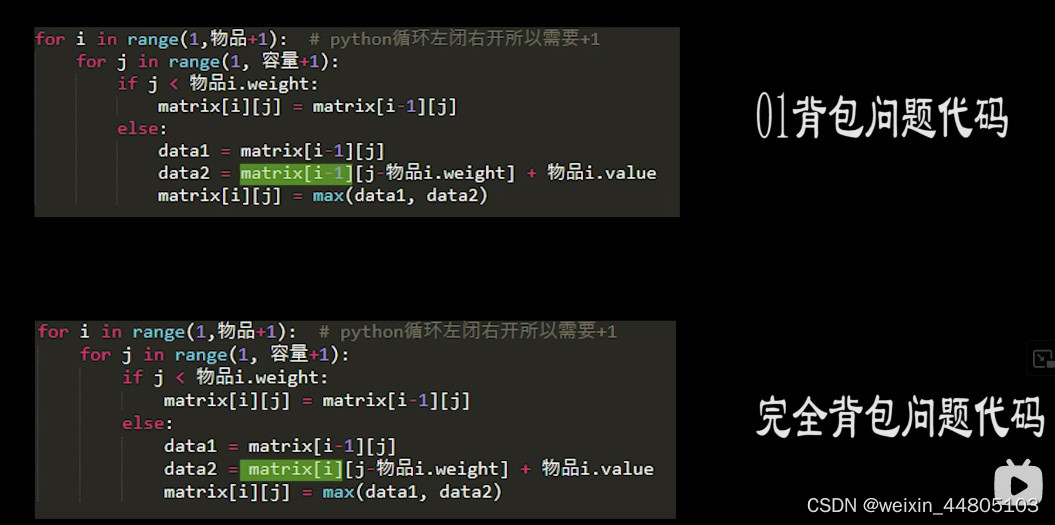
代码模板：
在完全背包问题，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！
关键在于：为什么完全背包容量是从小到大遍历
因为01里面的，选择当前商品时，从大到小遍历，dp[j - coins[i]]表示前(i-1)种物品被选中的情况。
完全里面，选择当前商品时，一个物品可以选多次，所以dp[j - coins[i]]表示当前商品以前也可以被选择。

518. 零钱兑换 II

纯完全背包求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序没关系
求凑出来的方案个数，且每个方案个数是为组合数。

在求装满背包有几种方案的时候，认清遍历顺序：
如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

1.是组合数：dp[j]：凑成总金额j的货币组合数为dp[j]
所以遍历当前容量时候
(1).选 dp[j-coins[i]] (2).不选，dp[j]

2.递推公式：dp[j] += dp[j - coins[i]];
3.初始化;j-coins[i] == 0的情况表示这个硬币刚好能选

class Solution {
    public int change(int amount, int[] coins) {
     
     int[] dp = new int[amount+1];
     dp[0] = 1; //初始化 
     for(int i=0;i<coins.length;i++){
         for(int j= coins[i] ;j<= amount ;j++){
            dp[j] = dp[j]+dp[j-coins[i]];
         }
     }
     return dp[amount];
    }
}

377. 组合总和 Ⅳ

如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

题目要求的是顺序不同的序列被视作不同的组合。
所以就是for循环背包，再循环物品

视频讲解：

这个讲了为啥外侧是包容量，因为顺序不同的序列被视作不同的组合

class Solution {
    public int combinationSum4(int[] nums, int target) {
        
   //存在数组中的元素能求出
     int[] dp = new int[target+1];
     dp[0] = 1;

     for(int i = 1;i<= target;i++){
         for(int j = 0;j<nums.length;j++){
            if(i>=nums[j]) {   // 只有当前包容量大于等于物品时候才考虑装不装
                dp[i] = dp[i] + dp[i-nums[j]];
            }
         }
     }
     return dp[target];
    }
}